Fast Computing of Conformal Mapping and Its Inverse of Bounded Multiply Connected Regions onto Second, Third and Fourth Categories of Koebe’s Canonical Slit Regions

Abstract

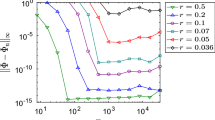
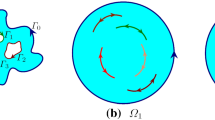
This paper presents a boundary integral method with the adjoint generalized Neumann kernel for conformal mapping of a bounded multiply connected region onto a disk with spiral slits region $\varOmega _1$. This extends the methods that have recently been given for mappings onto annulus with spiral slits region $\varOmega _2$, spiral slits region $\varOmega _3$, and straight slits region $\varOmega _4$ but with different right-hand sides. This paper also presents a fast implementation of the boundary integral equation method for computing numerical conformal mapping of bounded multiply connected region onto all four regions $\varOmega _1$, $\varOmega _2$, $\varOmega _3$, and $\varOmega _4$ as well as their inverses. The integral equations are solved numerically using combination of Nyström method, GMRES method, and fast multipole method (FMM). The complexity of this new algorithm is $O((m + 1)n)$, where $m+1$ is the multiplicity of the multiply connected region and n is the number of nodes on each boundary component. Previous algorithms require $O((m+1)^3 n^3)$ operations. The algorithm is tested on several test regions with complex geometries and high connectivities. The numerical results illustrate the efficiency of the proposed method.