Abstract
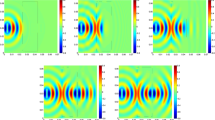
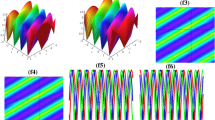
A new time second-order symmetric energy-conserved splitting FDTD scheme is proposed for solving the two-dimensional Maxwell’s equations in negative index metamaterials with Drude model. The scheme is proved to preserve the discrete electromagnetic energies in metamaterials and is of second order accuracy both in time and space. The proposed scheme also possesses the superconvergence and the second-order convergence for the discrete divergence. Numerical experiments confirm the theoretical results. Simulations of CW Gaussian beam interactions with double negative matematerials slabs and the electromagnetic waves propagating in metamaterials excited by sinusoidal point source are carried out to show supernormal phenomena in negative index metamaterials.






Similar content being viewed by others
References
Berénger, J.: A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 114, 185–200 (1994)
Bilotti, F., Sevgi, L.: Metamaterials: definitions, properties, applications, and fdtd-based modeling and simulation. Int. J. RF Microw. C. E. 22, 422–438 (2012)
Cevini, G., Oliveri, G., Raffetto, M.: Further comments on the performances of finite element simulators for the solution of electromagnetic problems involving metamaterials. Microw. Opt. Technol. Lett. 48, 2524–2529 (2006)
Chen, W., Li, X., Liang, D.: Energy-conserved splitting fdtd methods for maxwell’s equations. Numer. Math. 108, 445–485 (2008)
Chen, W., Li, X., Liang, D.: Symmetric energy-conserved splitting fdtd scheme for the maxwell’s equations. Commun. Comput. Phys. 6, 804–825 (2009)
Correia, D., Jin, J.: Theoretical analysis of left-handed metamaterials using fdtd-pml method. In: Proceedings of the 2003 SBMO/IEEE MTT-S International, vol. 2, pp. 1033–1036 (2003)
Correia, D., Jin, J.: 3d-fdtd-pml analysis of left-handed metamaterials. Microw. Opt. Technol. Lett. 40, 201–205 (2004)
Engheta, N., Ziolkowski, R.: A positive future for double-negative metamaterials. IEEE T. Microw. Theor. Y. 53, 1535–1556 (2005)
Engheta, N., Ziolkowski, R.: In Metamaterials: Physics and Engineering Explorations. Wiley, New York (2006)
Fang, N., Ying, L.: Stability analysis of fdtd to upml for time dependent maxwell equations. Sci. China Math. 52, 794–816 (2009)
Gao, L., Zhang, B., Liang, D.: The splitting finite-difference time-domain methods for maxwell’s equations in two dimensions. J. Comput. Appl. Math. 205, 207–230 (2007)
Goswami, C., Mukherjee, S., Karmakar, S., Pal, M., Ghatak, R.: Fdtd modeling of lorentzian dng metamaterials by auxiliary differential equation method. J. Electromagn. Anal. Appl. 6, 106–114 (2014)
Holden, A.: Towards some real applications for negative materials. Photonic Nanostruct. Fundam. Appl. 3, 96–99 (2005)
Huang, Y., Li, J.: Superconvergence of mixed finite element approximations to 3-d maxwell’s equations in metamaterials. J. Comput. Phys. 230, 8275–8289 (2011)
Joannopoulos, J., Meade, R., Winn, J.: Photonic crystals: modeling the flow of light. Princeton University Press, Princeton (1995)
Kosaka, H., Kawashima, T., Tomita, A., Notomi, M., Tamamura, T., Sato, T., Kawakami, S.: Superprism phenomena in photonic crystals. Phys. Rev. B 58, R10096–R10099 (1998)
Li, J., Shaw, S.: Schemes and estimates for the long-time numerical solution of maxwell’s equations for lorentz metamaterials. Int. J. Numer. Anal. Mod. 12, 343–365 (2015)
Li, J., Wood, A.: Finite element analysis for wave propagation in double negative metamaterials. J. Sci. Comput. 32, 263–286 (2007)
Li, W., Liang, D., Lin, Y.: A new energy-conserved s-fdtd scheme for maxwell’s equations in metamaterials. Int. J. Numer. Anal. Mod. 10, 775–794 (2013)
Martin, F., Toscano, A.: Guest editorial for special issue on metamaterials and special materials for electromagnetic applications and telecommunications. Microw. Opt. Technol. Lett. 48, 2481–2482 (2006)
Namiki, T.: A new fdtd algorithm based on alternating-direction implicit method. IEEE T. Microw. Theor. Y. 47, 2003–2007 (1999)
Nascimento, V., Jung, K., Borges, B., Teixeira, F.: A study on unconditionally stabel fdtd methods for the modeling of metamaterials. J. Lightwave Technol. 27, 4241–4249 (2009)
Pendry, J.: Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000)
Shelby, A., Smith, D., Schultz, S.: Experimental verification of a negative index of refraction. Science 292, 77–79 (2001)
Smith, D., Padilla, W., Vier, D., Nemat-Nasser, S., Schultz, S.: Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 84, 4184–4187 (2000)
Taflove, A., Brodwin, M.: Numerical solution of steady-state electromagnetic scattering problems using the time-dependent maxwells equations. IEEE T. Microw. Theor. Y. 23, 623–630 (1975)
Taflove, A., Hagness, S.: Computational electrodynamics: the finite-difference time-domain method. Artech House, Boston (2000)
Veselago, V.: The electrodynamics of substances with simultaneously negative values of \(\epsilon \) and \(\mu \). Sov. Phys. Usp. 47, 509–514 (1968)
Wang, M., Wu, J., Xu, J., Ge, D., Li, H., Feng, J.: Fdtd simulation on the interaction between gaussian beam and biaxial anisotropic metamaterial slabs. Int. J. Infrared Millim. 29, 167–178 (2008)
Yang, H., Song, H.: Symplectic fdtd method study left-handed material electromagnetic characteristics. Optik 124, 1716–1720 (2013)
Yee, K.: Numerical solution of initial boundary vallue problems involving maxwell’s equations in isotropic media. IEEE T. Antenn. Propa. G. 14, 302–307 (1966)
Zheng, F., Chen, Z., Zhang, J.: Toward the development of a three-dimensional unconditionally stable finite-difference time-domain method. IEEE T. Microw. Theor. Y. 48, 1550–1558 (2000)
Ziolkowski, R.: Design, fabrication, and testing of double negative metamaterials. IEEE Antenna Propag. 51, 1516 (2003)
Ziolkowski, R.: Pulsed and cw gaussian beam interactions with double negative metamaterial slabs. Opt. Express 11, 662–681 (2003)
Ziolkowski, R.: Propagation in and scattering from a matched metamaterial having a zero index of refraction. Phys. Rev. E 70, 046608 (2004)
Ziolkowski, R., Heyman, E.: Wave propagation in media having negative permittivity and permeability. Phys. Rev. E 64, 056625 (2001)
Acknowledgments
We would like to thank Professor Chi-Wang Shu and the referees for their valuable suggestions which have helped to improve the paper. D. Liang’s work was partly supported by Natural Sciences and Engineering Research Council of Canada.
Author information
Authors and Affiliations
Corresponding author
About this article
Cite this article
Li, W., Liang, D. Symmetric Energy-Conserved S-FDTD Scheme for Two-Dimensional Maxwell’s Equations in Negative Index Metamaterials. J Sci Comput 69, 696–735 (2016). https://doi.org/10.1007/s10915-016-0214-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0214-9