Skip to main content
Springer Nature Link
Log in

Two-Level Space–Time Domain Decomposition Methods for Flow Control Problems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

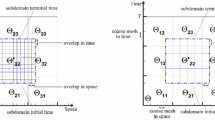
For time-dependent control problems, the class of sub-optimal algorithms is popular and the parallelization is usually applied in the spatial dimension only. In the paper, we develop a class of fully-optimal methods based on space–time domain decomposition methods for some boundary and distributed control of fluid flow and heat transfer problems. In the fully-optimal approach, we focus on the use of an inexact Newton solver for the necessary optimality condition arising from the implicit discretization of the optimization problem and the use of one-level and two-level space–time overlapping Schwarz preconditioners for the Jacobian system. We show that the numerical solution from the fully-optimal approach is generally better than the solution from the sub-optimal approach in terms of meeting the objective of the optimization problem. To demonstrate the robustness and parallel scalability and efficiency of the proposed algorithm, we present some numerical results obtained on a parallel computer with a few thousand processors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Akcelik, V., Biros, G., Draganescu, A., Ghattas, O., Hill, J.,Waanders, B.: Dynamic data-driven inversion for terascale simulations: real-time identification of airborne contaminants. In: Proceedings of Supercomputing, Seattle, WA (2005)

  2. Balay, S., Abhyankar, S., Adams, F.A., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Eijkhout, V., Gropp, W.D., Kaushik, D., Knepley, M.G., McInnes, L.C., Rupp, K., Smith, B.F., Zampini, S., Zhang, H.: PETSc Users Manual. Argonne National Laboratory, Illinois (2015)

    Google Scholar 

  3. Barker, A., Stoll, M.: Domain decomposition in time for PDE-constrained optimization. Comput. Phys. Commun. 197, 136–143 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bewley, T.R.: Flow control: new challenges for a new renaissance. Prog. Aerosp. Sci. 37, 21–58 (2001)

    Article  Google Scholar 

  5. Bewley, T.R., Temam, R., Ziane, M.: A general framework for robust control in fluid mechanics. Phys. D 138, 360–392 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  6. Biegler, L.T., Ghattas, O., Heinkenschloss, M., Keyes, D., Van Bloemen Waanders, B.: Real-Time PDE-Constrained Optimization, Computer Science Engineering. SIAM, Philadelphia (2007)

    Book  MATH  Google Scholar 

  7. Biros, G., Ghattas, O.: Parallel Lagrange–Newton–Krylov–Schur methods for PDE-constrained optimization, part I: the Krylov–Schur solver. SIAM J. Sci. Comput. 27, 687–713 (2005)

    Article  MATH  Google Scholar 

  8. Biros, G., Ghattas, O.: Parallel Lagrange–Newton–Krylov–Schur methods for PDE-constrained optimization, part II: the Lagrange–Newton solver and its application to optimal control of steady viscous flows. SIAM J. Sci. Comput. 27, 714–739 (2005)

    Article  MATH  Google Scholar 

  9. Cai, X.-C., Gropp, W.D., Keyes, D.E., Melvin, R.G., Young, D.P.: Parallel Newton–Krylov–Schwarz algorithms for the transonic full potential equation. SIAM J. Sci. Comput. 19, 246–265 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chen, R., Cai, X.-C.: Parallel one-shot Lagrange–Newton–Krylov–Schwarz algorithms for shape optimization of steady incompressible flows. SIAM J. Sci. Comput. 34, B584–B605 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chen, R., Cai, X.-C.: A parallel two-level domain decomposition based one-shot method for shape optimization problems. Int. J. Numer. Meth. Eng. 99, 945–965 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Deng, X.M., Cai, X.-C., Zou, J.: A parallel space-time domain decomposition method for unsteady source inversion problems. Inverse Probl. Imag. 9, 1069–1091 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Deng, X.M., Cai, X.-C., Zou, J.: Two-level space–time domain decomposition methods for three-dimensional unsteady inverse source problems. J. Sci. Comput. 67, 860–882 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Dembo, R.S., Eisenstat, S.C., Steihaug, T.: Inexact Newton methods. SIAM J. Numer. Anal. 19, 400–408 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  15. Dennis, J.E., Schnabel, R.B.: Numerical Methods for Unconstrained Optimization and Nonlinear Equations. SIAM, Philadelphia (1996)

    Book  MATH  Google Scholar 

  16. Du, X., Sarkis, M., Schaerer, C.E., Szyld, D.B.: Inexact and truncated parareal-in-time Krylov subspace methods for parabolic optimal control problems. ETNA 40, 36–57 (2013)

    MathSciNet  MATH  Google Scholar 

  17. Eisenstat, S.C., Walker, H.F.: Globally convergent inexact Newton method. SIAM J. Optim. 4, 393–422 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  18. Evans, K.J., Knoll, D.A.: Temporal accuracy of phase change convection simulations using the JFNK-SIMPLE algorithm. Int. J. Numer. Meth. Fluids 55, 637–655 (2007)

    Article  MATH  Google Scholar 

  19. Ghattas, O., Bark, J.-H.: Optimal control of two- and three-dimensional incompressible Navier-Stokes flows. J. Comput. Phys. 136, 231–244 (1997)

    Article  MATH  Google Scholar 

  20. Gunzburger, M., Hou, L., Svobodny, T.: The approximation of boundary control problems for fluid flows with an application to control by heating and cooling. Comput. Fluids 22, 239–251 (1993)

    Article  MATH  Google Scholar 

  21. Gunzburger, M., Manservis, S.: The velocity tracking problem for Navier-Stokes flows with bounded distributed control. SIAM J. Control Optim. 37, 1913–1945 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  22. Gunzburger, M., Manservis, S.: The velocity tracking problem for Navier-Stokes flow with boundary control. SIAM J. Numer. Anal. 39, 594–634 (2000)

    MathSciNet  Google Scholar 

  23. Gunzburger, M., Manservis, S.: Analysis and approximation of the velocity tracking problem for Navier–Stokes flows with distributed control. SIAM J. Numer. Anal. 37, 481–1512 (2000)

    MathSciNet  Google Scholar 

  24. Gunzburger, M.: Perspectives in Flow Control and Optimization, 1st edn. SIAM, Philadelphia (2003)

    MATH  Google Scholar 

  25. Heinkenschloss, M.: A time-domain decomposition iterative method for the solution of distributed linear quadratic optimal control problems. J. Comput. Appl. Math. 173, 169–198 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  26. Hinze, M., Köster, M., Turek S.: A hierarchical space-time solver for distributed control of the stokes equation. Priority Programme 1253, Technical Report SPP1253-16-01 (2008)

  27. Hinze, M., Köster, M., Turek, S.: Space–Time Newton-Multigrid Strategies for Nonstationary Distributed and Boundary Flow Control Problems. Springer, New York (2014)

    Book  MATH  Google Scholar 

  28. Ito, K., Ravindran, S.S.: Optimal control of thermally convected flows. SIAM J. Sci. Comput. 19, 1847–1869 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  29. Knoll, D.A., Chacón, L., Margolin, L.G., Mousseau, V.A.: On balanced approximations for time integration of multiple time scale systems. J. Comput. Phys. 185, 583–611 (2003)

    Article  MATH  Google Scholar 

  30. Knoll, D.A., Keyes, D.E.: Jacobian-free Newton–Krylov methods: a survey of approaches and applications. J. Comput. Phys. 193, 357–397 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  31. Kunisch, K., Sachs, E.W.: Reduced SQP methods for parameter identification problems. SIAM J. Numer. Anal. 29, 1793–1820 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  32. Kupfer, F.S., Sachs, E.W.: Numerical solution of a nonlinear parabolic control problem by a reduced SQP method. Comput. Optim. Appl. 1, 113–135 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  33. Li, S., Cai, X.-C.: Convergence analysis of two-level space–time additive Schwarz method for parabolic equations. SIAM J. Numer. Anal. 53, 2727–2751 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  34. Moin, P., Bewley, T.R.: Feedback control of turbulence. Appl. Mech. Rev. 47, 3–13 (1994)

    Article  Google Scholar 

  35. Prudencio, E., Byrd, R., Cai, X.-C.: Parallel full space SQP Lagrange–Newton–Krylov–Schwarz algorithms for PDE-constrained optimization problems. SIAM J. Sci. Comput. 27, 1305–1328 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  36. Prudencio, E., Cai, X.-C.: Parallel multilevel restricted Schwarz preconditioners with pollution removing for PDE-constrained optimization. SIAM J. Sci. Comput. 29, 964–985 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  37. Quartapelle, L.: Numerical Solution of the Incompressible Navier–Stokes Equations. International Series of Numerical Mathematics, vol. 113. Birkhäuser Verlag, Basel (1996)

    Google Scholar 

  38. Ravindran, S.S.: Adaptive reduced-order controllers for a thermal flow system using proper orthogonal decomposition. SIAM J. Sci. Comput. 23, 1924–1942 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  39. Ravindran, S.S.: Numerical approximation of optimal control of unsteady flows using SQP and time decomposition. Int. J. Numer. Meth. Fluids 45, 21–42 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  40. Saad, Y.: Iterative Methods for Sparse Linear Systems, 2nd edn. SIAM, Philadelphia (2003)

    Book  MATH  Google Scholar 

  41. Schulz, V.: Solving discretized optimization problems by partially reduced SQP methods. Comput. Vis. Sci. 1, 83–96 (1998)

    Article  MATH  Google Scholar 

  42. Smith, B., Bjørstad, P., Gropp, W.: Domain Decomposition: Parallel Multilevel Methods for Elliptic Partial Differential Equations. Cambridge University Press, Cambridge (1996)

    MATH  Google Scholar 

  43. Stoll, M., Wathen, A.: All-at-once solution of time-dependent PDE-constrained optimization problems. Technical Report. University of Oxford (2010)

  44. Stoll, M., Wathen, A.: All-at-once solution of time-dependent Stokes control. J. Comput. Phys. 232, 498–515 (2013)

    Article  MathSciNet  Google Scholar 

  45. Toselli, A., Widlund, O.: Domain Decomposition Methods-Algorithms and Theory. Springer, Berlin (2005)

    Book  MATH  Google Scholar 

  46. Wu, Y., Cai, X.-C.: A fully implicit domain decomposition based ALE framework for three-dimensional fluid-structure interaction with application in blood flow computation. J. Comput. Phys. 258, 524–537 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  47. Yan, Y., Keyes, D.E.: Smooth and robust solutions for Dirichlet boundary control of fluid-solid conjugate heat transfer problems. J. Comput. Phys. 281, 759–786 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  48. Yang, C., Cai, X.-C.: Parallel multilevel methods for implicit solution of shallow water equations with nonsmooth topography on cubed-sphere. J. Comput. Phys. 230, 2523–2539 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  49. Yang, C., Cai, X.-C.: A scalable fully implicit compressible Euler solver for mesoscale nonhydrostatic simulation of atmospheric flows. SIAM J. Sci. Comput. 35, S23–S47 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  50. Yang, H., Cai, X.-C.: Scalable parallel algorithms for boundary control of thermally convective flows. 13th IEEE International Workshop on Parallel and Distributed Scientific and Engineering Computing, Shanghai, pp. 1387–1396 (2012)

  51. Yang, H., Cai, X.-C.: Parallel fully implicit two-grid Lagrange–Newton–Krylov–Schwarz methods for distributed control of unsteady incompressible flows. Int. J. Numer. Meth. Fluids 72, 1–21 (2013)

    Article  Google Scholar 

  52. Yang, H., Hwang, F.-N., Cai, X.-C.: Nonlinear preconditioning techniques for full-space Lagrange–Newton solution of PDE-constrained optimization problems. SIAM J. Sci. Comput. (2016) (to appear)

  53. Yang, H., Prudencio, E., Cai, X.-C.: Fully implicit Lagrange–Newton–Krylov–Schwarz algorithms for boundary control of unsteady incompressible flows. Int. J. Numer. Meth. Eng. 91, 644–665 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors would like to express their appreciations to the anonymous reviewers for the invaluable comments that have greatly improved the quality of the manuscript. This research was supported by the NSFC Grants 11571100 and 91330111. Haijian Yang was also supported in part by the NSFC Grant 11272352 and the Planned Science and Technology Project of Hunan Province under grant 2015JC3055.

Author information

Authors and Affiliations

  1. College of Mathematics and Econometrics, Hunan University, Changsha, 410082, Hunan, People’s Republic of China

    Haijian Yang

  2. Department of Computer Science, University of Colorado Boulder, Boulder, CO, 80309, USA

    Xiao-Chuan Cai

Authors
  1. Haijian Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiao-Chuan Cai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xiao-Chuan Cai.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, H., Cai, XC. Two-Level Space–Time Domain Decomposition Methods for Flow Control Problems. J Sci Comput 70, 717–743 (2017). https://doi.org/10.1007/s10915-016-0263-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-016-0263-0

Keywords