Method of Lines Transpose: An Efficient Unconditionally Stable Solver for Wave Propagation

Abstract

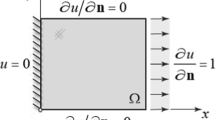
Building upon recent results obtained in Causley and Christlieb (SIAM J Numer Anal 52(1):220–235, 2014), Causley et al. (Math Comput 83(290):2763–2786, 2014, Method of lines transpose: high order L-stable O(N) schemes for parabolic equations using successive convolution, 2015), we describe an efficient second-order, unconditionally stable scheme for solving the wave equation, based on the method of lines transpose (MOL$^T$), and the resulting semi-discrete (i.e. continuous in space) boundary value problem. In Causley and Christlieb (SIAM J Numer Anal 52(1):220–235, 2014), unconditionally stable schemes of high order were derived, and in Causley et al. (Method of lines transpose: high order L-stable O(N) schemes for parabolic equations using successive convolution, 2015) a high order, fast $\mathcal {O}(N)$ spatial solver was derived, which is matrix-free and is based on dimensional-splitting. In this work, are interested in building a wave solver, and our main concern is the development of boundary conditions. We demonstrate all desired boundary conditions for a wave solver, including outflow boundary conditions, in 1D and 2D. The scheme works in a logically Cartesian fashion, and the boundary points are embedded into the regular mesh, without incurring stability restrictions, so that boundary conditions are imposed without any reduction in the order of accuracy. We demonstrate how the embedded boundary approach works in the cases of Dirichlet and Neumann boundary conditions. Further, we develop outflow and periodic boundary conditions for the MOL$^T$ formulation. Our solver is designed to couple with particle codes, and so special attention is also paid to the implementation of point sources, and soft sources which can be used to launch waves into waveguides.

Appendices

Appendix 1: Summary Table For Second-Order Wave Solver

Wave equation	Dispersive scheme, $\alpha = \frac{2}{c \varDelta t}$:
$\frac{1}{c^{2}}\frac{\partial u}{\partial t} - \nabla ^{2} u = S(x,t)$	$\left( -\frac{1}{\alpha ^{2}}\nabla ^{2}+1 \right) \left( u^{n+1}+2u^{n}+u^{n-1}\right) = 4u^{n} + \frac{4}{\alpha ^{2}}S(x,t^{n})$
To	Diffusive scheme, $\alpha = \frac{\sqrt{2}}{c \varDelta t}$:
Modified Helmholtz equation	$\left( -\frac{1}{\alpha ^{2}}\nabla ^{2}+1 \right) u^{n+1} = \frac{1}{2}\left( 5u^{n}-4u^{n-1}+u^{n-2}\right) + \frac{1}{\alpha ^{2}} S(x,t^{n+1})$
Dimensionally split	$\left( -\frac{1}{\alpha ^{2}}\nabla ^{2}+1 \right) u=f$ $\Rightarrow$
Modified Helmholtz equation	$\left( -\frac{1}{\alpha ^{2}}\frac{\partial ^{2}}{\partial x^{2}}+1 \right) \left( -\frac{1}{\alpha ^{2}}\frac{\partial ^{2}}{\partial y^{2}}+1 \right) u = f$ $\Rightarrow$
(2D)	$\left( -\frac{1}{\alpha ^{2}}\frac{\partial ^{2}}{\partial x^{2}}+1 \right) w = f$,    $\left( -\frac{1}{\alpha ^{2}}\frac{\partial ^{2}}{\partial y^{2}}+1 \right) u = w$
1D integral solution	$\left( -\frac{1}{\alpha ^{2}}\frac{d^{2}}{dx^{2}}+1 \right) u = f$ on (a, b) $\Rightarrow$
	$u(x) = \frac{\alpha }{2}\int _{a}^{b} f(x')e^{-\alpha |x-x'|} \, dx' + Ae^{-\alpha (x-a)} + Be^{-\alpha (b-x)}$
	$= I[f](x) + Ae^{-\alpha (x-a)} + Be^{-\alpha (b-x)}$
1D BC correction coefficients
Dirichlet:	$A = \frac{(u_{a}-I_{a})-\mu (u_{b}-I_{b})}{1-\mu ^{2}}$, $B = \frac{(u_{b}-I_{b})-\mu (u_{a}-I_{a})}{1-\mu ^{2}}$
$u(a) = u_{a}$, $u(b) = u_{b}$
Neumann:	$A = \frac{\mu (v_{b}+\alpha I_{b})-(v_{a}-\alpha I_{a})}{\alpha \left( 1-\mu ^2\right) }$, $B = \frac{(v_{b}+\alpha I_{b})-\mu (v_{a}-\alpha I_{a})}{\alpha \left( 1-\mu ^2\right) }$
$u'(a) = v_{a}$, $u'(b) = v_{b}$
Periodic:	$A = \frac{I_{b}}{1-\mu }$, $B = \frac{I_{a}}{1-\mu }$
$u(a) = u(b)$, $u'(a) = u'(b)$
	$I_{a} = I[f](a)$, $I_{b} = I[f](b)$, $\mu = e^{-\alpha (b-a)}$
Fast convolution algorithm	$a = x_{0}< x_{1}< \cdots < x_{N} = b$,
	$x_{j+1} - x_{j}+ \varDelta x$, $j=0,...,N-1$
	$I_{j} = I[f](x_{j}) = \frac{\alpha }{2}\int _{a}^{b} f(x')e^{-\alpha |x_{j}-x'|} \, dx' = I^{L}_{j} + I^{R}_{j}$
	$I^{L}_{j} = \frac{\alpha }{2}\int _{a}^{x_{j}} f(x')e^{-\alpha |x_{j}-x'|} \, dx'$, $I^{R}_{j} = \frac{\alpha }{2}\int _{x_{j}}^{b} f(x')e^{-\alpha |x_{j}-x'|} \, dx'$
	$I^{L}_{0}=0$, $I^{L}_{j} = e^{-\alpha \varDelta x} I^{L}_{j-1} + J^{L}_{j}$,
	$J^{L}_{j} = \frac{\alpha }{2}\int _{x_{j-1}}^{x_{j}} f(x')e^{-\alpha |x_{j}-x'|} \, dx'$, $j=1,...,N$
	$I^{R}_{N}=0$, $I^{R}_{j} = e^{-\alpha \varDelta x} I^{R}_{j+1} + J^{R}_{j}$,
	$J^{R}_{j} = \frac{\alpha }{2}\int _{x_{j}}^{x_{j+1}} f(x')e^{-\alpha |x_{j}-x'|} \, dx'$, $j=N-1,...,0$
Second-order quadrature	$J^{R}_{j} = Pf(x_{j})+Qf(x_{j+1}) + R(f(x_{j+1})-2f(x_{j})+f(x_{j-1}))$
	$J^{L}_{j} = Pf(x_{j})+Qf(x_{j-1}) + R(f(x_{j+1})-2f(x_{j})+f(x_{j-1}))$
	$P = 1-\frac{1-d}{\nu }$, $Q = -d+\frac{1-d}{\nu }$, $R = \frac{1-d}{\nu ^{2}}-\frac{1+d}{2\nu }$
	$\nu = \alpha \varDelta x$, $d = e^{-\nu }$

Appendix 2: Treatment of Point Sources, and Soft Sources

We now consider the inclusion of source terms. We present the algorithm in 1D for simplicity, and observe that the extensions to multiple dimensions are analogous to those shown for dimensional splitting presented in Sect. 2. The implementation of a soft source $\sigma (t)$ at $x = x_s$ is accomplished by prescribing the source condition

$$\begin{aligned} u(x_s,t) = \sigma (t). \end{aligned}$$

(35)

However, it can be shown that if we set

$$\begin{aligned} S(x,t)= \frac{2}{c}\sigma '(t) \delta (x-x_s) \end{aligned}$$

(36)

and insert it into the wave equation, then the soft source condition (35) is satisfied, and the solutions are equivalent. Thus, a soft source is nothing more than a point source, whose time-varying field is integrated by the wave equation.

Upon convolving this source term with the Green’s function according to (4), we find

$$\begin{aligned} I\left[ \frac{1}{\alpha ^2}S\right] (x)=&\frac{1}{2\alpha }\int _a^b \left( \frac{2}{c}\sigma '(t_n)\delta (x-x_s) \right) e^{-\alpha |x-y|}dy \\ =&\frac{\varDelta t}{\beta } \sigma '(t_n) e^{-\alpha |x-x_s|}, \end{aligned}$$

where the definition of $\alpha = \beta /(c\varDelta t)$ has been utilized. It is often the case that taking the analytical derivative $\sigma '(t_n)$ is to be avoided, for various reasons. In this case, any finite difference approximation which is of the desired order of accuracy can be substituted.