Abstract
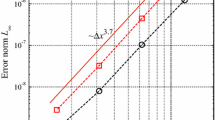
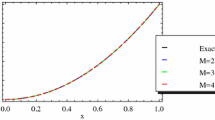
This paper presents several hybrid algorithms to preserve the global energy of the Benjamin equation. The Benjamin equation is a non-local partial differential equation involving the Hilbert transform. For this sake, quite few structure-preserving integrators have been proposed so far. Our schemes are derived based on an extended multi-symplectic Hamiltonian system of the Benjamin equation by using Fourier pseudospectral method, finite element method and wavelet collocation method spatially coupled with the AVF method temporally. The local and global properties of the proposed schemes are studied. Numerical experiments are presented to demonstrate the conservative properties of the proposed numerical methods and study the evolutions of the numerical solutions of solitary waves and wave breaking.

















Similar content being viewed by others
References
Albert, J.P., Bona, J.L., Restrepo, J.M.: Solitary-wave solutions of the Benjamin equation. SIAM J. Appl. Math. 59, 2139–2161 (1999)
Benjamin, T.B.: A new kind of solitary wave. J. Fluid Mech. 245, 401–411 (1992)
Benjamin, T.B.: Solitary and periodic waves of a new kind. Phil. Trans. R. Soc. A 354, 1775–1806 (1996)
Boyd, J.P., Xu, Z.J.: Comparison of three spectral methods for the Benjamin–Ono equation: Fourier pseudospectral, rational Christov functions and Gaussian radial basis functions. Wave Motion 48, 702–706 (2011)
Bridges, T.J.: Multi-symplectic structures and wave propagation. Math. Proc. Camb. Philos. Soc. 121, 147–190 (1997)
Calvo, D.C., Akylas, T.R.: On interfacial gravity-capillary solitary waves of the Benjamin type and their stability. Phys. Fluids 15, 1261–1270 (2003)
Celledoni, E., Grimm, V., McLachlan, R.I., McLaren, D.I., O’Neale, D., Owren, B., Quispel, G.R.W.: Preserving energy resp. dissipation in numerical PDEs using the “Average Vector Field” method. J. Comput. Phys. 231, 6670–6789 (2012)
Dodd, R.K., Eilbeck, J.C., Gibbon, J.D., Morris, H.C.: Solitons and nonlinear wave equations. Academic Press, London (1982)
Dougalis, V.A., Durán, A., Mitsotakis, D.E.: Numerical solution of the Benjamin equation. Wave Motion 52, 194–215 (2015)
Dougalis, V.A., Durán, A., Mitsotakis, D.E.: Numerical approximation of solitary waves of the Benjamin equation. Math. Comput. Simul. 127, 56–79 (2016)
Gong, Y.Z., Wang, Y.S.: An energy-preserving wavelet collocation method for general multi-symplectic formulations of Hamiltonian PDEs. Commun. Comput. Phys. 20, 1313–1339 (2016)
Kalisch, H., Bona, J.L.: Models for internal waves in deep water. Discrete Contin. Dyn. Syst. 6, 1–20 (2000)
Kinugasa, K., Miyatake, Y., Matsuo, T.: Structure-preserving integrators for the Benjamin-type equations. arXiv preprint arXiv: 1507.08359 (2015)
Lamb, G.L.: Elements of Soliton Theory. Wiley, New York (1980)
Linares, F.: \(L^2\) global well-posedness of the initial value problem associated to the Benjamin equation. J. Differ. Equ. 152, 377–393 (1999)
Linares, F., Scialom, M.: On generalized Benjamin type equations. Discrete Contin. Dyn. Syst. 12, 161–174 (2005)
McLachlan, R.I., Quispel, G.R.W., Robidoux, N.: Geometric integration using discrete gradients. Philos. Trans. R. Soc. A 357, 1021–1046 (1999)
Thomée, V., Vasudeva Murthy, A.S.: A numerical method for the Benjamin–Ono equation. BIT 38, 597–611 (1998)
Quispel, G.R.W., McLaren, D.I.: A new class of energy-preserving numerical integration methods. J. Phys. A 41, 045206 (2008)
Saito, N., Beylkin, G.: Multiresolution repersentations using the autocorrelation functions of compactly supported wavelets. IEEE Trans. Signal Process. 41, 3584–3590 (1993)
Zhu, H.J., Tang, L.Y., Song, S.H., Tang, Y.F., Wang, D.S.: Symplectic wavelet collocation method for Hamiltonian wave equations. J. Comput. Phys. 229, 2550–2572 (2010)
Acknowledgements
This work is supported by the Jiangsu Collaborative Innovation Center for Climate Change, the National Natural Science Foundation of China (Grant Nos. 11271195, 41231173) and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Song, Y., Wang, Y. Energy-Preserving Algorithms for the Benjamin Equation. J Sci Comput 72, 605–622 (2017). https://doi.org/10.1007/s10915-017-0371-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-017-0371-5