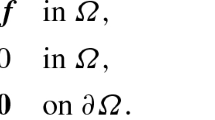Abstract
We show that two widely used Galerkin formulations for second-order elliptic problems provide approximations which are actually superclose, that is, their difference converges faster than the corresponding errors. In the framework of linear elasticity, the two formulations correspond to using either the stiffness tensor or its inverse the compliance tensor. We find sufficient conditions, for a wide class of methods (including mixed and discontinuous Galerkin methods), which guarantee a supercloseness result. For example, for the HDG\(_{k}\) method using polynomial approximations of degree \({k>0}\), we find that the difference of approximate fluxes superconverges with order \({k+2}\) and that the difference of the scalar approximations superconverges with order \({k+3}\). We provide numerical results verifying our theoretical results.

Similar content being viewed by others
References
Arbogast, T., Wheeler, M.F., Yotov, I.: Mixed finite elements for elliptic problems with tensor coefficients as cell-centered finite differences. SIAM J. Numer. Anal. 34(2), 828–852 (1997)
Arnold, N.D.: An interior penalty finite element method with discontinuous elements. SIAM J. Numer. Anal. 19(4), 742–760 (1982)
Brezzi, F., Douglas Jr., J., Marini, L.D.: Two families of mixed finite elements for second order elliptic problems. Numer. Math. 47(2), 217–235 (1985)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer Series in Computational Mathematics, vol. 15. Springer, New York (1991)
Castillo, P., Cockburn, B., Perugia, I., Schötzau, D.: An a priori error analysis of the local discontinuous Galerkin method for elliptic problems. SIAM J. Numer. Anal. 38(5), 1676–1706 (2000)
Ciarlet, P.G.: The finite element method for elliptic problems, volume 40 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia. Reprint of the 1978 original [North-Holland, Amsterdam; MR0520174 (58 #25001)] (2002)
Cockburn, B.: Static condensation, hybridization, and the devising of the HDG methods. In: Barrenechea, G.R., Brezzi, F., Cagniani, A., Georgoulis, E.H. (eds) Building Bridges: Connections and Challenges in Modern Approaches to Numerical Partial Differential Equations, volume 114 of Lecture Notes of Computer Science Engineering, pp. 129–177. Springer, Berlin, 2016. LMS Durham Symposia funded by the London Mathematical Society. Durham, 8–16 July (2014)
Cockburn, B., Di-Pietro, D.A., Ern, A.: Bridging the hybrid high-order and hybridizable discontinuous Galerkin methods. ESAIM Math. Model. Numer. Anal. 50(3), 635–650 (2016)
Cockburn, B., Dong, B., Guzmán, J.: A superconvergent LDG-hybridizable Galerkin method for second-order elliptic problems. Math. Comput. 77(264), 1887–1916 (2008)
Cockburn, B., Dong, B., Guzmán, J.: A superconvergent LDG-hybridizable Galerkin method for second-order elliptic problems. Math. Comput. 77, 1887–1916 (2008)
Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)
Cockburn, B., Gopalakrishnan, J., Sayas, F.-J.: A projection-based error analysis of HDG methods. Math. Comput. 79, 1351–1367 (2010)
Cockburn, B., Guzmán, J., Wang, H.: Superconvergent discontinuous Galerkin methods for second-order elliptic problems. Math. Comput. 78, 1–24 (2009)
Cockburn, B., Shen, J.: A hybridizable discontinuous Galerkin method for the \(p\)-Laplacian. SIAM J. Sci. Comput. 38(1), A545–A566 (2016)
Cockburn, B., Shi, K.: Superconvergent HDG methods for linear elasticity with weakly symmetric stresses. IMA J. Numer. Anal. 33(3), 747–770 (2013)
Di-Pietro, D.A., Ern, A.: A hybrid high-order locking-free method for linear elasticity on general meshes. Comput. Methods Appl. Mech. Eng. 283, 1–21 (2015)
Di-Pietro, D.A., Ern, A.: Hybrid high-order methods for variable-diffusion problems on general meshes. C. R. Acad. Sci Paris Ser. I 353, 31–34 (2015)
Di-Pietro, D.A., Ern, A., Lemaire, S.: An arbitrary-order and compact-stencil discretization of diffusion on general meshes based on local reconstruction operators. Comput. Methods Appl. Math. 14(4), 461–472 (2014)
Raviart, P.-A., Thomas, J.M.: A mixed finite element method for 2nd order elliptic problems. In: Mathematical Aspects of Finite Element Methods (Proc. Conf., Consiglio Naz. delle Ricerche (C.N.R.), Rome, 1975), Lecture Notes in Mathematics, Vol. 606, pp. 292–315. Springer, Berlin (1977)
Soon, S.-C.: Hybridizable discontinuous Galerkin methods for solid mechanics. Ph.D. thesis, University of Minnesota, Minneapolis (2008)
Soon, S.-C., Cockburn, B., Stolarski, H.K.: A hybridizable discontinuous Galerkin method for linear elasticity. Int. J. Numer. Methods Eng. 80(8), 1058–1092 (2009)
Acknowledgements
We wish to the thank one of the referees for constructive criticism leading to a better presentation of the material, including the discussion about the IP methods which we originally did not consider.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cockburn, B., Sánchez, M.A. & Xiong, C. Supercloseness of Primal-Dual Galerkin Approximations for Second Order Elliptic Problems. J Sci Comput 75, 376–394 (2018). https://doi.org/10.1007/s10915-017-0538-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-017-0538-0