Skip to main content
Springer Nature Link
Log in

Local Discontinuous Galerkin Methods for the Boussinesq Coupled BBM System

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

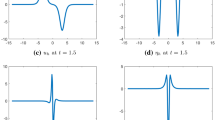
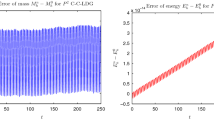
Abstract

Nonlinear dispersive wave equations model a substantial number of physical systems that admit special solutions such as solitons and solitary waves. Due to the complex nature of the nonlinearity and dispersive effects, high order numerical methods are effective in capturing the physical system in computation. In this paper, we consider the Boussinesq coupled BBM system, and propose local discontinuous Galerkin (LDG) methods for solving the BBM system. For the proposed LDG methods, we provide two different choices of numerical fluxes, namely the upwind and alternating fluxes, as well as establish their stability analysis. The error estimate for the linearized BBM system is carried out for the LDG methods with the alternating flux. To present a time discretization that conserves the Hamiltonian numerically, the midpoint rule with a nontrivial nonlinear term in the discretization is proposed. Both Hamiltonian conserving and dissipating time discretizations are implemented, with multiple combinations of numerical flux and time discretization tested numerically. Numerical examples are provided to demonstrate the accuracy, long-time simulation, and Hamiltonian conservation properties of the proposed LDG methods for the coupled BBM system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. The length of this subinterval is arbitrary. We wish to capture the peak in the interval, and have the “tails” near the peak to be close to zero.

References

  1. Alazman, A., Albert, J., Bona, J., Chen, M., Wu, J.: Comparisons between the BBM equation and a Boussinesq system. Adv. Differ. Equ. 11(2), 121–166 (2006)

    MathSciNet  MATH  Google Scholar 

  2. Bassi, F., Rebay, S.: A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier–Stokes equations. J. Comput. Phys. 131, 267–279 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  3. Benjamin, T., Bona, J., Mahony, J.: Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 272(1220), 47–78 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bona, J., Chen, M.: A Boussinesq system for two-way propagation of nonlinear dispersive waves. Physica D 116, 191–224 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bona, J., Chen, M., Saut, J.: Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. i. J. Nonlinear Sci. 12, 283–318 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bona, J., Chen, M., Saut, J.: Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media: II. The nonlinear theory. Nonlinearity 17, 925–952 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bona, J.L., Chen, H., Karakashian, O.A., Xing, Y.: Conservative discontinuous Galerkin methods for the Generalized Korteweg–de Vries equation. Math. Comput. 82, 1401–1432 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Boussinesq, J.: Théorie de l’intumescence liquide appelée onde solitaire ou de translation se propageant dans un canal rectangulaire. Comptes Rendus de l’Acadmie de Sciences 72, 755–759 (1871)

    MATH  Google Scholar 

  9. Chen, M.: Exact traveling-wave solutions to bidirectional wave equations. Int. J. Theor. Phys. 37(5), 1547–1567 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chen, R.M., Yue, L.: On the ill-posedness of a weakly dispersive one-dimensional Boussinesq system. J. d’Analyse Mathématique 121(1), 299–316 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chou, C.-S., Shu, C.-W., Xing, Y.: Optimal energy conserving local discontinuous Galerkin methods for second-order wave equation in heterogeneous media. J. Comput. Phys. 272, 88–107 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cockburn, B., Hou, S., Shu, C.-W.: The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws IV: the multidimensional case. Math. Comput. 54, 545–581 (1990)

    MathSciNet  MATH  Google Scholar 

  13. Cockburn, B., Karniadakis, G., Shu, C.-W.: The development of discontinuous galerkin methods. In: Cockburn, B., Karniadakis, G., Shu, C.-W. (eds) Discontinuous Galerkin Methods: Theory, Computation and Applications, pp. 3–50. Lecture Notes in Computational Science and Engineering, Part I: Overview, vol. 11, Springer, Berlin (2000)

  14. Cockburn, B., Lin, S.-Y., Shu, C.-W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one dimensional systems. J. Comput. Phys. 84, 90–113 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  15. Cockburn, B., Shu, C.-W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws II: general framework. Math. Comput. 52, 411–435 (1989)

    MathSciNet  MATH  Google Scholar 

  16. Cockburn, B., Shu, C.W.: The local discontinuous Galerkin finite element method for convection-diffusion systems. SIAM J. Numer. Anal. 35, 2440–2463 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  17. Dougalis, V., Mitsotakis, D., Saut, J.: On initial-boundary value problems for a Boussinesq system of BBM–BBM type in a plane domain. Discret. Contin. Dyn. Syst. Ser. A 23(4), 1191–1204 (2009)

    MathSciNet  MATH  Google Scholar 

  18. Gottlieb, S.: On high order strong stability preserving Runge Kutta and multi step time discretizations. J. Sci. Comput. 25(1 and 2), 105–128 (1999)

    MathSciNet  MATH  Google Scholar 

  19. Liu, H., Huang, Y.-Q., Yi, N.-Y.: A direct discontinuous Galerkin method for the Degasperis–Procesi equation. Methods Appl. Anal. 21, 83–106 (2014)

    Article  MATH  Google Scholar 

  20. Liu, H., Xing, Y.: An invariant preserving discontinuous Galerkin method for the Camassa–Holm equation. SIAM J. Sci. Comput. 38, A1919–A1934 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-479, Los Alamos Scientific Laboratory (1973)

  22. Spiteri, R.J., Ruuth, S.J.: A new class of optimal high-order strong-stability-preserving time discretization methods. SIAM J. Numer. Anal. 40, 469–491 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  23. Wang, H., Shu, C.-W., Zhang, Q.: Stability and error estimates of local discontinuous Galerkin methods with implicit–explicit time-marching for advection–diffusion problems. SIAM J. Numer. Anal. 53, 206–227 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Xing, Y., Chou, C.-S., Shu, C.-W.: Energy conserving local discontinuous Galerkin methods for wave propagation problems. Inverse Probl. Imaging 7, 967–986 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  25. Xu, Y., Shu, C.-W.: Error estimates of the semi-discrete local discontinuous galerkin method for nonlinear convection–diffusion and KdV equations. Comput. Methods Appl. Mech. Eng. 196, 3805–3822 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  26. Xu, Y., Shu, C.-W.: Local discontinuous Galerkin methods for high-order time-dependent partial differential equations. Commun. Comput. Phys. 7, 1–46 (2010)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of California Riverside, Riverside, CA, 92521, USA

    Joshua Buli

  2. Department of Mathematics, Ohio State University, Columbus, OH, 43210, USA

    Yulong Xing

Authors
  1. Joshua Buli
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yulong Xing
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yulong Xing.

Additional information

Y. Xing: The work of this author was partially supported by the NSF Grants DMS-1621111, DMS-1753581 and ONR Grant N00014-16-1-2714.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buli, J., Xing, Y. Local Discontinuous Galerkin Methods for the Boussinesq Coupled BBM System. J Sci Comput 75, 536–559 (2018). https://doi.org/10.1007/s10915-017-0546-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-017-0546-0

Keywords