Skip to main content
SpringerLink
Log in

A Sixth-Order Weighted Essentially Non-oscillatory Schemes Based on Exponential Polynomials for Hamilton–Jacobi Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

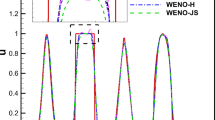
In this study, we present a new sixth-order finite difference weighted essentially non-oscillatory (WENO) scheme for solving Hamilton–Jacobi equations. The proposed scheme recovers the maximal approximation order in smooth regions without loss of accuracy at critical points. We incorporate exponential polynomials into the scheme to obtain better approximation near steep gradients without spurious oscillations. In order to design nonlinear weights based on exponential polynomials, we suggest an alternative approach to construct Lagrange-type exponential functions reproducing the cell-average values of exponential basis functions. Using the Lagrange-type exponential functions, we provide a detailed analysis of the approximation order of the proposed WENO scheme. Compared to other WENO schemes, the proposed scheme is simpler to implement, yielding better approximations with lower computational costs. A number of numerical experiments are presented to demonstrate the performance of the proposed scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Abgrall, R.: Numerical discretization of the first-order Hamilton–Jacobi equation on triangular meshes. Commun. Pure Appl. Math. 49, 1339–1373 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  2. Augoula, S., Abgrall, R.: High order numerical discretization for Hamilton–Jacobi equations on triangular meshes. J. Sci. Comput. 15, 197–229 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  3. Balsara, D.S., Shu, C.W.: Monotonicity preserving WENO schemes with increasingly high-order of accuracy. J. Comput. Phys. 160, 405–452 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  4. Barth, T.J., Sethian, J.A.: Numerical schemes for the Hamilton–Jacobi and level set equations on triangulated domains. J. Comput. Phys. 145, 1–40 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bell, J.B., Colella, P., Glaz, H.M.: A second order projection method for the incompressible Navier–Stokes equations. J. Comput. Phys. 85, 257–283 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  6. Borges, R., Carmona, M., Costa, B., Don, W.S.: An improved WENO scheme for hyperbolic conservation laws. J. Comput. Phys. 227, 3191–3211 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bryson, S., Levy, D.: High-order semi-discrete central-upwind schemes for multi-dimensional Hamilton–Jacobi equations. J. Comput. Phys. 189, 63–87 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bryson, S., Levy, D.: High-order central WENO schemes for multidimensional Hamilton–Jacobi equations. SIAM J. Numer. Anal. 41, 1339–1369 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bryson, S., Levy, D.: Mapped WENO and weighted power ENO reconstructions in semi-discrete central schemes for Hamilton–Jacobi equations. App. Numer. Math. 56, 1211–1224 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Castro, M., Costa, B., Don, W.S.: High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws. J. Comput. Phys. 230, 1766–1792 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Cecil, T., Qian, J., Osher, S.: Numerical methods for high dimensional Hamilton–Jacobi equations using radial basis functions. J. Comput. Phys. 196, 327–347 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cheng, Y., Shu, C.-W.: A discontinuous Galerkin finite element method for directly solving the Hamilton–Jacobi equations. J. Comput. Phys. 223, 398–415 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cheng, Y., Wang, Z.: A new discontinuous Galerkin finite element method for directly solving the Hamilton–Jacobi equations. J. Comput. Phys. 268, 134–153 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  14. Crandall, M.G., Evans, L.C., Lions, P.L.: Some properties of viscosity solutions of Hamilton–Jacobi equations. Trans. Am. Math. Soc. 282, 487–502 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  15. Crandall, M.G., Lions, P.L.: Viscosity solutions of Hamilton–Jacobi equations. Trans. Am. Math. Soc. 277, 1–42 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  16. Crandall, M.G., Lions, P.L.: Two approximations of solutions of Hamilton–Jacobi equations. Math. Comput. 43, 1–19 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  17. Crandall, M.G., Ishii, H., Lions, P.L.: User’s guide to viscosity solutions of second order partial equations. Bull. Am. Math. Soc. (N.S) 27, 1–67 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  18. Gerolymos, G.A., Sénéchal, D., Vallet, I.: Very-high-order WENO schemes. J. Comput. Phys. 228, 8481–8524 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Guo, W., Li, F., Qiu, J.: Local-structure-preserving discontinuous Galerkin methods with Lax–Wendroff type time discretizations for Hamilton–Jacobi equations. J. Sci. Comput. 47(2), 239–257 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Ha, Y., Kim, C., Lee, Y.J., Yoon, J.: Mapped WENO schemes based on a new smoothness indicator for Hamilton–Jacobi equations. J. Math. Anal. Appl. 394, 670–682 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ha, Y., Kim, C.H., Lee, Y.J., Yoon, J.: An improved weighted essentially non-osciallatory scheme with a new smoothness indicator. J. Comput. Phys. 232, 68–86 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Ha, Y., Lee, Y.J., Yoon, J.: Modified essentially non-osciallatory scheme based on exponential polynomial interpolation for hyperbolic conservation laws. SIAM J. Numer. Anal. 52(2), 864–893 (2013)

    Article  MATH  Google Scholar 

  23. Ha, Y., Kim, C., Yang, H., Yoon, J.: Sixth-order weighted essentially nonoscillatory schemes based on exponential polynomials. SIAM J. Sci. Comput. 38, A1984–A2017 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Harten, A., Engquist, B., Osher, S., Chakravarthy, S.: Uniformly high-order accurate essentially non-oscillatory schemes III. J. Comput. Phys. 71, 231–303 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  25. Henrick, A.K., Aslam, T.D., Powers, J.M.: Mapped weighted-essentially-non-oscillatory schemes: achieving optimal order near critical points. J. Comput. Phys. 207, 542–567 (2005)

    Article  MATH  Google Scholar 

  26. Hu, X.Y., Wang, Q., Adams, N.A.: An adaptive central-upwind weighted essentially non-oscillatory scheme. J. Comput. Phys. 229, 8952–8965 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  27. Hu, C., Shu, C.-W.: A discontinuous Galerkin finite element method for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21, 666–690 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  28. Jiang, G., Peng, D.: Weighted ENO schemes for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21, 2126–2143 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  29. Jiang, G.-S., Shu, C.-W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  30. Jin, S., Xin, Z.: Numerical passage from systems of conservation laws to Hamilton–Jacobi equations, and relaxation schemes. SIAM J. Numer. Anal. 35, 2385–2404 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  31. Kurganov, A., Tadmor, E.: New high-resolution semi-discrete central schemes for Hamilton–Jacobi equations. J. Comput. Phys. 160, 720–742 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  32. Lafon, F., Osher, S.: High order two dimensional nonoscillatory methods for solving Hamilton–Jacobi scalar equations. J. Comput. Phys. 123, 235–253 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  33. Lepsky, O., Hu, C., Shu, C.-W.: Analysis of the discontinuous Galerkin method for Hamilton–Jacobi equations. Appl. Numer. Math. 33, 423–434 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  34. Li, X.G., Chan, C.K.: High-order schemes for Hamilton–Jacobi equations on triangular meshes. J. Comput. Appl. Math. 167, 227–241 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  35. Lin, C.-T., Tadmor, E.: High-resolution non-oscillatory central schemes for approximate Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21, 2163–2186 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  36. Osher, S., Sethian, J.: Fronts propagating with curvature dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 79, 12–49 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  37. Osher, S., Shu, C.-W.: High-order essentially non-oscillatory schemes for Hamilton–Jacobi equations. SIAM J. Numer. Anal. 28, 907–922 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  38. Qiu, J., Shu, C.-W.: Hermite WENO schemes for Hamilton–Jacobi equations. J. Comput. Phys. 204, 82–99 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  39. Qiu, J.: WENO schemes with Lax–Wendroff type time discretizations for Hamilton–Jacobi equations. J. Comput. Appl. Math. 200, 591–605 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  40. Qiu, J.: Hermite WENO schemes with Lax–Wendroff type time discretizations for Hamilton–Jacobi equations. J. Comput. Math. 25, 131–144 (2007)

    MathSciNet  MATH  Google Scholar 

  41. Serna, S., Qian, J.: Fifth order weighted power-ENO methods for Hamilton–Jacobi equations. J. Sci. Comput. 29, 57–81 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  42. Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock capturing schemes. J. Comput. Phys. 77, 439–471 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  43. Souganidis, P.E.: Approximation schemes for viscosity solutions of Hamilton–Jacobi equations. J. Differ. Equ. 59, 1–43 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  44. Sussman, M., Smereka, P., Osher, S.: A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 114, 146–159 (1994)

    Article  MATH  Google Scholar 

  45. Yamaleev, N.K., Carpenter, M.H.: A systematic methodology for constructing high-order energy stable WENO schemes. J. Comput. Phys. 228, 4248–4272 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  46. Yan, J., Osher, S.: A local discontinuous Galerkin method for directly solving Hamilton–Jacobi equations. J. Comput. Phys. 230, 232–244 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  47. Yuan, L., Shu, C.-W.: Discontinuous Galerkin method based on non-polynomial approximation spaces. J. Comput. Phys. 218, 295–323 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  48. Zalesak, S.: Fully multidimensional flux-corrected transport algorithms for fluids. J. Comput. Phys. 31, 335–362 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  49. Zhang, Y.-T., Shu, C.-W.: High-order WENO schemes for Hamilton–Jacobi equations on triangular meshes. SIAM J. Sci. Comput. 24, 1005–1030 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  50. Zheng, F., Qiu, J.: Directly solving the Hamilton–Jacobi equations by Hermite WENO schemes. J. Comput. Phys. 307, 423–445 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  51. Zhu, J., Qiu, J.: Trigonometric WENO schemes for hyperbolic conservation laws and highly oscillatory problems. Commun. Comput. Phys. 8, 1242–1263 (2010)

    MathSciNet  MATH  Google Scholar 

  52. Zhu, J., Qiu, J.: WENO schemes and their application as limiters for RKDG methods based on trigonometric approximation spaces. J. Sci. Comput. 55, 606–644 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Youngsoo Ha was supported by the grant NRF-2017R1D1A1B03034912 through the National Research Foundation of Korea and Chang Ho Kim was supported by Konkuk University. Jungho Yoon was supported by the grant NRF-2015R1A5A1009350 through the National Research Foundation of Korea and the MOTIE 10048720 through the Ministry of Trade, Industry and Energy of Korea.

Author information

Authors and Affiliations

  1. Department of Mathematics, Seoul National University, Seoul, South Korea

    Youngsoo Ha

  2. Department of Computer Engineering, Glocal Campus, Konkuk University, Chungju, 380-701, South Korea

    Chang Ho Kim

  3. Department of Mathematics, Ewha W. University, Seoul, 120-750, South Korea

    Hyoseon Yang & Jungho Yoon

Authors
  1. Youngsoo Ha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chang Ho Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hyoseon Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jungho Yoon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hyoseon Yang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ha, Y., Kim, C.H., Yang, H. et al. A Sixth-Order Weighted Essentially Non-oscillatory Schemes Based on Exponential Polynomials for Hamilton–Jacobi Equations. J Sci Comput 75, 1675–1700 (2018). https://doi.org/10.1007/s10915-017-0603-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-017-0603-8

Keywords

Search

Navigation