Abstract
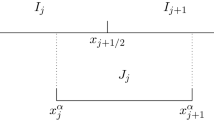
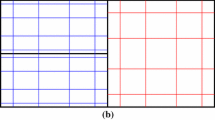
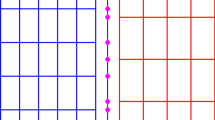
In this paper, we first present a family of high order central discontinuous Galerkin methods defined on unstructured overlapping meshes for the two-dimensional conservation laws. The primal mesh is a triangulation of the computational domain, while the dual mesh is a quadrangular partition which is formed by connecting an interior point and the three vertexes of each triangle on the primal mesh. We prove the \(L^2\) stability of the present method for linear equation. Then we design and analyze high order maximum-principle-satisfying central discontinuous Galerkin methods for two-dimensional scalar conservation law, and high order positivity-preserving central discontinuous Galerkin methods for two-dimensional compressible Euler systems. The performance of the proposed methods is finally demonstrated through a set of numerical experiments.












Similar content being viewed by others
References
Brio, M., Zakharian, A.R., Webb, G.M.: Two-dimensional Riemann solver for Euler equations of gas dynamics. J. Comput. Phys. 167, 177–195 (2001)
Chen, G., Feng, M.: Stabilized finite element methods for the Biot’s consolidation problem. Adv. Appl. Math. Mech. 10, 77–99 (2018)
Chen, G., Hu, W.W., Shen, J.G., Singler, J.R., Zhang, Y.W., Zheng, X.B.: An HDG method for distributed control of convection diffusion PDEs. J. Comput. Appl. Math. 343, 643–661 (2018)
Chen, Y., Luo, Y., Feng, M.: Analysis of a discontinuous Galerkin method for the Biot’s consolidation problem. Appl. Math. Comput. 219, 9043–9056 (2013)
Cheng, Y., Li, F., Qiu, J., Xu, L.: Positivity-preserving DG and central DG methods for ideal MHD equations. J. Comput. Phys. 238, 255–280 (2013)
Cockburn, B., Lin, S.-Y., Shu, C.-W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one-dimensional systems. J. Comput. Phys. 84, 90–113 (1989)
Cockburn, B., Shu, C.-W.: The Runge–Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys. 141, 199–224 (1998)
Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. Springer, Berlin (2000)
Deng, X.-L., Li, M.: Simulating compressible two-medium flows with sharp-interface adaptive Runge–Kutta discontinuous Galerkin methods. J. Sci. Comput. 74, 1347–1368 (2018)
Dong, H., Li, M.: A reconstructed central discontinuous Galerkin-finite element method for the fully nonlinear weakly dispersive Green–Naghdi model. Appl. Numer. Math. 110, 110–127 (2016)
Dong, H., Lv, M., Li, M.: A reconstructed central discontinuous Galerkin method for conservation laws. Comput. Fluids 153, 76–84 (2017)
Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability preserving high order time discretization methods. SIAM Rev. 43, 89–112 (2001)
Jiang, G.-S., Shu, C.-W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228 (1996)
Kim, H.H., Chung, E.T., Lee, C.S.: A staggered discontinuous Galerkin method for the Stokes system. SIAM J. Numer. Anal. 51, 3327–3350 (2013)
Li, F., Yakovlev, S.: A central discontinuous Galerkin method for Hamilton–Jacobi equations. J. Sci. Comput. 45, 404–428 (2010)
Li, F., Xu, L.: Arbitrary order exactly divergence-free central discontinuous Galerkin methods for ideal MHD equations. J. Comput. Phys. 231, 2655–2675 (2012)
Li, F., Xu, L., Yakovlev, S.: Central discontinuous Galerkin methods for ideal MHD equations with exactly divergence-free magnetic field. J. Comput. Phys. 230, 4828–4847 (2011)
Li, M., Guyenne, P., Li, F., Xu, L.: High order well-balanced CDG-FE methods for shallow water waves by a Green-Naghdi model. J. Comput. Phys. 257, 169–192 (2014)
Li, M., Chen, A.: High order central discontinuous Galerkin-finite element methods for the Camassa–Holm equation. Appl. Math. Comput. 227, 237–245 (2014)
Li, M., Li, F.Z., Xu, L.: Maximum-principle-satisfying and positivity-preserving high order CDG methods for conservation laws. SIAM J. Sci. Comput. 38, A3720–A3740 (2016)
Li, M., Guyenne, P., Li, F., Xu, L.: A positivity-preserving well-balanced central discontinuous Galerkin method for the nonlinear shallow water equations. J. Sci. Comput. 711, 994–1034 (2017)
Li, M., Jiang, Y., Dong, H.: High order well-balanced central local discontinuous Galerkin-finite element methods for solving the Green–Naghdi model. Appl. Math. Comput. 315, 113–130 (2017)
Li, X.: Boundedness in a two-dimensional attraction-repulsion system with nonlinear diffusion. Math. Methods Appl. Sci. 39, 289–301 (2016)
Liu, Y., Shu, C.-W., Tadmor, E., Zhang, M.: Central discontinuous Galerkin methods on overlapping cells with a nonoscillatary hierarchical reconstruction. SIAM J. Numer. Anal. 45, 2442–2467 (2007)
Liu, Y., Shu, C.-W., Tadmor, E., Zhang, M.: Central local discontinuous Galerkin methods on overlapping cells for diffusion equations. ESAIM: Math. Model. Numer. Anal. 45, 1009–1032 (2011)
Luo, Y., Feng, M., Xu, Y.: A stabilized mixed discontinuous Galerkin method for the incompressible miscible displacement problem. Bound. Value Probl. 2011, 48 (2011)
Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-479, Los Alamos Scientific Laboratory (1973)
Ren, X., Wu, J., Xiang, Z., Zhang, Z.: Global existence and decay of smooth solution for the 2-D MHD equation without magnetic diffusion. J. Funct. Anal. 267, 503–541 (2014)
Shu, C.-W.: Essentially Non-oscillatory and Weighted Essentially Non-oscillatory Schemes for Hyperbolic Conservation Laws, ICASE Report. Brown University, Rhode Island (1997)
Sun, M., Takayama, K.: The formation of a secondary shock wave behind a shock wave diffracting at a convex corner. Shock Waves 7, 287–295 (1997)
Tang, H., Warnecke, G.: A Runge–Kutta discontinuous Galerkin method for the Euler equations. Comput. Fluids 34, 375–398 (2005)
Vukovic, S., Sopta, L.: ENO and WENO schemes with the exact conservation property for one-dimensional shallow water equations. J. Comput. Phys. 179, 593–621 (2002)
Wang, C., Zhang, X., Shu, C.-W., Ning, J.: Robust high order discontinuous Galerkin schemes for two-dimensional gaseous detonations. J. Comput. Phys. 231, 653–665 (2012)
Xu, Z., Liu, Y.: New central and central discontinuous Galerkin schemes on overlapping cells of unstructured grids for solving ideal magnetohydrodynamic equations with globally divergence-free magnetic field. J. Comput. Phys. 327, 203–224 (2016)
Zhang, X., Shu, C.-W.: On maximum-principle-satisfying high order schemes for scalar conservation laws. J. Comput. Phys. 229, 3091–3120 (2010)
Zhang, X., Shu, C.-W.: On positivity-preserving high order discontinuous Galerkin schemes for compressible Euler equations on rectangular meshes. J. Comput. Phys. 229, 8918–8934 (2010)
Zhang, X., Xia, Y., Shu, C.-W.: Maximum-principle-satisfying and positivity-preserving high order discontinuous Galerkin schemes for conservation laws on triangular meshes. J. Sci. Comput. 50, 29–62 (2012)
Acknowledgements
ML is partially supported by a NSFC (Grant No. 11501062, 11871139). HD is partially supported by a NSFC (Grant No. 11701055). LX is partially supported by a Key Project of the Major Research Plan of NSFC (Grant No. 91630205) and a NSFC (Grant No. 11771068).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, M., Dong, H., Hu, B. et al. Maximum-Principle-Satisfying and Positivity-Preserving High Order Central DG Methods on Unstructured Overlapping Meshes for Two-Dimensional Hyperbolic Conservation Laws. J Sci Comput 79, 1361–1388 (2019). https://doi.org/10.1007/s10915-018-00895-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-00895-x
Keywords
- Conservation laws
- Central discontinuous Galerkin methods
- Unstructured overlapping meshes
- Maximum principle
- Positivity preserving