Skip to main content
Springer Nature Link
Log in

Convergence of the MAC Scheme for the Stokes/Darcy Coupling Problem

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

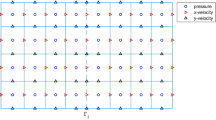
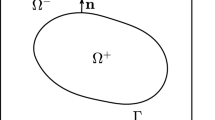
In this paper, we extend the MAC scheme for Stokes problem to the Stokes/Darcy coupling problem. The interface conditions between two separate regions are discretized and well-incorporated into the MAC grid setting. We first perform the stability analysis of the scheme for the velocity in both Stokes and Darcy regions and establish the stability for the pressure in both regions by considering an analogue of discrete divergence problem. Following the similar analysis on stability, we perform the error estimates for the velocity and the pressure in both regions. The theoretical results show the first-order convergence of the scheme in discrete \(L^2\) norms for both velocity and the pressure in both regions. Moreover, in fluid region, the first-order convergence for the x-derivative of velocity component u and the y-derivative of velocity component v is also obtained in discrete \(L^2\) norms. However, numerical tests show one order better for the velocity in Stokes region and the pressure in Darcy region.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Arbogast, T., Brunson, D.S.: A computational method for approximating a Darcy–Stokes system governing a vuggy porous medium. Comput. Geosci. 11, 207–218 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  2. Tlupova, S., Cortez, R.: Boundary integral solutions of coupled Stokes and Darcy flows. J. Comput. Phys. 228, 158–179 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  3. Chen, Q.: Stable and convergent approximation of two-dimensional vector fields on unstructured meshes. J. Comput. Appl. Math. 307, 284–306 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  4. Chou, S.H.: Analysis and convergence of a covolume method for the generalized Stokes problem. Math. Comp. 66, 85–104 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cai, M., Mu, M., Xu, J.: Preconditioning techniques for a mixed Stokes/Darcy model in porous media applications. J. Comput. Appl. Math. 233, 346–355 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cao, Y., Gunzburger, M., Hu, X., Hua, F., Wang, X., Zhao, W.: Finite element approximations for Stokes–Darcy flow with Beavers–Joseph interface conditions. SIAM J. Numer. Anal. 47, 4239–4256 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cao, Y., Gunzburger, M., Hu, X., Wang, X.: Parallel, non-iterative, multi-physics domain decomposition methods for time-dependent Stokes–Darcy systems. Math. Comput. 83, 1617–1644 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  8. Camano, J., Gatica, G.N., Oyarza, R., Ruiz-Baier, R., Venegas, P.: New fully-mixed finite element methods for the Stokes–Darcy coupling. Comput. Methods Appl. Mech. Eng. 295, 362–395 (2015)

    Article  MathSciNet  Google Scholar 

  9. Chidyagwai, P., Ladenheim, S., Szyld, D.: Constraint preconditioning for the coupled Stokes–Darcy system. SIAM J. Sci. Comput. 38, A668–A690 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chidyagwai, P., Riviere, B.: Numerical modelling of coupled surface and subsurface flow systems. Adv. Water Res. 33, 92–105 (2010)

    Article  Google Scholar 

  11. Chen, W., Gunzburger, M., Sun, D., Wang, X.: An efficient and long-time accurate third-order algorithm for the Stokes–Darcy system. Numer. Math. 134, 857–879 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Discacciati, M., Quarteroni, A.: Convergence analysis of a subdomain iterative method for the finite element approximation of the coupling of Stokes and Darcy equations. Comput. Visual Sci. 6, 93–103 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Discacciati, M., Quarteroni, A.: Navier–Stokes/Darcy coupling: modeling, analysis, and numerical approximation. Rev. Mat. Complut. 22, 315–426 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  14. Gatica, G., Oyarzua, R., Sayas, F.: Analysis of fully-mixed finite element methods for the Stokes–Darcy coupled problem. Math. Comput. 80, 1911–1948 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  15. Girault, V., Vassilev, D., Yotov, I.: Mortar multiscale finite element methods for Stokes–Darcy flows. Numer. Math. 127, 93–165 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  16. Harlow, F.H., Welsh, J.E.: Numerical calculation of time-dependent viscous incompressible flow of fluid with a free interface. Phys. Fluids 8, 2181–2189 (1965)

    Article  Google Scholar 

  17. Han, H., Wu, X.: A new mixed finite element formulation and the MAC method for the Stokes equations. SIAM J. Numer. Anal. 35, 650–571 (1998)

    Article  MathSciNet  Google Scholar 

  18. Hessari, P.: Pseudospectral least squares method for Stokes–Darcy equations. SIAM J. Numer. Anal. 53, 1195–1213 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Kanschat, G., Rivire, B.: A strongly conservative finite element method for the coupling of Stokes and Darcy flow. J. Comput. Phys. 229, 5933–5943 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  20. Layton, W.J., Schieweck, F., Yotov, I.: Coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 40(6), 2195–2218 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  21. Li, Z.: An augmented Cartesian grid method for Stokes–Darcy fluid–structure interactions. Int. J. Numer. Meth. Eng. 106, 556–575 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, J., Sun, S.: The superconvergence phenomenon and proof of the MAC scheme for the Stokes equations on non-uniform rectangular meshes. J. Sci. Comput. 65, 341–362 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mu, M., Xu, J.: A two-grid method of a mixed Stokes–Darcy model for coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 45, 1801–1813 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Nicolaides, R.A.: Analysis and convergence of the MAC scheme I. The linear problem. SIAM J. Numer. Anal. 29, 1579–1591 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  25. Rui, H., Li, X.: Stability and superconvergence of MAC scheme for Stokes equations on nonuniform grids. SIAM J. Numer. Anal. 55(3), 1135–1158 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  26. Rui, H., Liu, W.: A two-grid block-centered finite difference method MAC scheme forDarcy–Forchheimer flow in porous media. SIAM J. Numer. Anal. 53(4), 1941–1962 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  27. Rui, H., Pan, H.: A block-centered finite difference method for the Darcy–Forchheimer. SIAM J. Numer. Anal. 50(5), 2612–2631 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  28. Rui, H., Pan, H.: A block-centered finite difference method for slightly compressible Darcy–Forchheimer flow in porous media. J. Sci. Comput. 73(1), 70–92 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  29. Shin, D., Strikwerda, J.C.: Inf-sup conditions for finite-difference approximations of the Stokes equations. J. Aust. Math. Soc. Ser. B 39, 121–134 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  30. Wang, W., Xu, C.: Spectral methods based on new formulations for coupled Stokes and Darcy equations. J. Comput. Phys. 257, 126–142 (2014)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The work of M.-C. Lai was supported in part by Ministry of Science of Technology of Taiwan under research grant MOST-104-2115-M-009-014-MY3 while M.-C. Shiue was supported in part by the Grant MOST-104-2115-M-009-012-MY2. K.C. Ong was supported in part by NCTU Taiwan Elite Internship Program at National Chiao Tung University and NCTS.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, National Chiao Tung University, 1001 Ta Hsueh Road, Hsinchu, 300, Taiwan

    Ming-Cheng Shiue, Kian Chuan Ong & Ming-Chih Lai

Authors
  1. Ming-Cheng Shiue
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Kian Chuan Ong
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ming-Chih Lai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ming-Cheng Shiue.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shiue, MC., Ong, K.C. & Lai, MC. Convergence of the MAC Scheme for the Stokes/Darcy Coupling Problem. J Sci Comput 76, 1216–1251 (2018). https://doi.org/10.1007/s10915-018-0660-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0660-7

Keywords