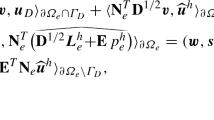Skip to main content
Springer Nature Link
Log in

Discontinuous Galerkin Method with Staggered Hybridization for a Class of Nonlinear Stokes Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

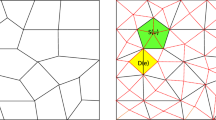
In this paper, we present a discontinuous Galerkin method with staggered hybridization to discretize a class of nonlinear Stokes equations in two dimensions. The utilization of staggered hybridization is new and this approach combines the features of traditional hybridization method and staggered discontinuous Galerkin method. The main idea of our method is to use hybrid variables to impose the staggered continuity conditions instead of enforcing them in the approximation space. Therefore, our method enjoys some distinctive advantages, including mass conservation, optimal convergence and preservation of symmetry of the stress tensor. We will also show that, one can obtain superconvergent and strongly divergence-free velocity by applying a local postprocessing technique on the approximate solution. We will analyze the stability and derive a priori error estimates of the proposed scheme. The resulting nonlinear system is solved by using the Newton’s method, and some numerical results will be demonstrated to confirm the theoretical rates of convergence and superconvergence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Boersma, B.J.: A staggered compact finite difference formulation for the compressible Navier–Stokes equations. J. Comput. Phys. 208(2), 675–690 (2005)

    Article  MATH  Google Scholar 

  2. Boffi, D., Brezzi, F., Fortin, M., et al.: Mixed Finite Element Methods and Applications, vol. 44. Springer, New York (2013)

    MATH  Google Scholar 

  3. Brenner, S.C.: Poincaré–Friedrichs inequalities for piecewise \(H^1\) functions. SIAM J. Numer. Anal. 41(1), 306–324 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bustinza, R., Gatica, G.N.: A local discontinuous Galerkin method for nonlinear diffusion problems with mixed boundary conditions. SIAM J. Sci. Comput. 26(1), 152–177 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cheung, S.W., Chung, E., Kim, H.H., Qian, Y.: Staggered discontinuous Galerkin methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 302, 251–266 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chung, E., Cockburn, B., Fu, G.: The staggered DG method is the limit of a hybridizable DG method. Part II: The Stokes flow. J. Sci. Comput. 66(2), 870–887 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chung, E.T., Du, J., Yuen, M.C.: An adaptive SDG method for the Stokes system. J. Sci. Comput. 70, 766–792 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chung, E.T., Engquist, B.: Optimal discontinuous Galerkin methods for wave propagation. SIAM J. Numer. Anal. 44(5), 2131–2158 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chung, E.T., Engquist, B.: Optimal discontinuous Galerkin methods for the acoustic wave equation in higher dimensions. SIAM J. Numer. Anal. 47(5), 3820–3848 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chung, E. T., Lam, M. F., Lam, C. Y.: A staggered discontinuous Galerkin method for a class of nonlinear elliptic equations. arXiv preprint arXiv:1610.02331, (2016)

  11. Chung, E.T., Qiu, W.: Analysis of an SDG method for the incompressible Navier–Stokes equations. SIAM J. Numer. Anal. 55(2), 543–569 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  12. Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. SIAM, Philadelphia (2002)

    Book  MATH  Google Scholar 

  13. Ciarlet, P.G., Glowinski, R., Xu, J.: Numerical Methods for Non-Newtonian Fluids: Special Volume, vol. 16. Elsevier, Amsterdam (2010)

    Google Scholar 

  14. Cockburn, B., Fu, G., Qiu, W.: A note on the devising of superconvergent hdg methods for Stokes flow by m-decompositions. IMA J. Numer. Anal. 37(2), 730–749 (2017)

    MathSciNet  Google Scholar 

  15. Cockburn, B., Gopalakrishnan, J.: The derivation of hybridizable discontinuous galerkin methods for stokes flow. SIAM J. Numer. Anal. 47(2), 1092–1125 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  16. Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Cockburn, B., Kanschat, G., Schötzau, D., Schwab, C.: Local discontinuous Galerkin methods for the Stokes system. SIAM J. Numer. Anal. 40(1), 319–343 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  18. Girault, V., Rivière, B., Wheeler, M.: A discontinuous Galerkin method with nonoverlapping domain decomposition for the Stokes and Navier–Stokes problems. Math. Comput. 74(249), 53–84 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Grinevich, P.P., Olshanskii, M.A.: An iterative method for the Stokes-type problem with variable viscosity. SIAM J. Sci. Comput. 31(5), 3959–3978 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Isaac, T., Stadler, G., Ghattas, O.: Solution of nonlinear Stokes equations discretized by high-order finite elements on nonconforming and anisotropic meshes, with application to ice sheet dynamics. SIAM J. Sci. Comput. 37(6), B804–B833 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kim, H.H., Chung, E.T., Lee, C.S.: A staggered discontinuous Galerkin method for the Stokes system. SIAM J. Numer. Anal. 51(6), 3327–3350 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Lee, J.J., Kim, H.H.: Analysis of a staggered discontinuous Galerkin method for linear elasticity. J. Sci. Comput. 66(2), 625–649 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  23. Liu, C., Walkington, N.J.: Convergence of numerical approximations of the incompressible Navier–Stokes equations with variable density and viscosity. SIAM J. Numer. Anal. 45(3), 1287–1304 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Nečas, J.: Introduction to the Theory of Nonlinear Elliptic Equations, vol. 52. Teubner, Braunschweig (1983)

    MATH  Google Scholar 

  25. Nguyen, N., Peraire, J., Cockburn, B.: A hybridizable discontinuous galerkin method for Stokes flow. Comput. Methods Appl. Mech. Eng. 199(9), 582–597 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  26. Qiu, W., Shen, J., Shi, K.: An HDG method for linear elasticity with strong symmetric stresses. arXiv preprint arXiv:1312.1407, (2013)

  27. Qiu, W., Shi, K.: A superconvergent HDG method for the incompressible Navier–Stokes equations on general polyhedral meshes. IMA J. Numer. Anal. 36(4), 1943–1967 (2016)

    Article  MathSciNet  Google Scholar 

  28. Raviart, P.-A., Girault, V.: Finite Element Approximation of the Navier–Stokes Equations. Springer Verlag, New York (1979)

    MATH  Google Scholar 

  29. Schubert, G., Turcotte, D.L., Olson, P.: Mantle Convection in the Earth and Planets. Cambridge University Press, Cambridge (2001)

    Book  Google Scholar 

  30. Tavelli, M., Dumbser, M.: A staggered semi-implicit discontinuous Galerkin method for the two dimensional incompressible Navier–Stokes equations. Appl. Math. Comput. 248, 70–92 (2014)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The research of Eric Chung and Xiao-Ping Wang is partially supported by a NSFC/RGC Joint Research Scheme (Project: N_HKUST620/15). The research of Eric Chung is partially supported by Hong Kong RGC General Research Fund (Project number: 14317516).

Author information

Authors and Affiliations

  1. Yau Mathematical Sciences Center, Tsinghua University, Beijing, China

    Jie Du

  2. Department of Mathematics, The Chinese University of Hong Kong, Sha Tin, Hong Kong SAR

    Eric T. Chung & Ming Fai Lam

  3. Department of Mathematics, The Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong SAR

    Xiao-Ping Wang

Authors
  1. Jie Du
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Eric T. Chung
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ming Fai Lam
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Xiao-Ping Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jie Du.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Du, J., Chung, E.T., Lam, M.F. et al. Discontinuous Galerkin Method with Staggered Hybridization for a Class of Nonlinear Stokes Equations. J Sci Comput 76, 1547–1577 (2018). https://doi.org/10.1007/s10915-018-0676-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0676-z

Keywords