Abstract
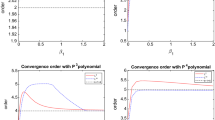
A hybrid staggered discontinuous Galerkin method is developed for the Korteweg–de Vries equation. The equation is written into a system of first order equations by introducing auxiliary variables. Two sets of finite element functions are introduced to approximate the solution and the auxiliary variables. The staggered continuity of the two finite element function spaces gives a natural flux condition and trace value on the element boundaries in the derivation of Galerkin approximation. On the other hand, to deal with the third order derivative term an hybridization idea is used and additional flux unknowns are introduced. The auxiliary variables can be eliminated in each element and the resulting algebraic system on the solution and the additional flux unknowns is solved. Stability of the semi discrete form is proven for various boundary conditions. Numerical results present the optimal order of \(L^2\)-errors of the proposed method for a given polynomial order.






Similar content being viewed by others
References
Benjamin, T.B., Bona, J.L., Mahony, J.J.: Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond. Ser. A 272(1220), 47–78 (1972)
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications. Springer Series in Computational Mathematics, vol. 44. Springer, Heidelberg (2013)
Bona, J.L., Dougalis, V.A., Karakashian, O.A.: Fully discrete Galerkin methods for the Korteweg–de Vries equation. Comput. Math. Appl. Ser. A 12(7), 859–884 (1986)
Chan, H.N., Chung, E.T.: A staggered discontinuous Galerkin method with local TV regularization for the Burgers equation. Numer. Math. Theory Methods Appl. 8(4), 451–474 (2015)
Chertock, A., Levy, D.: A particle method for the KdV equation. In: Proceedings of the Fifth International Conference on Spectral and High Order Methods (ICOSAHOM-01) (Uppsala), vol. 17, pp. 491–499 (2002)
Cheung, S.W., Chung, E., Kim, H.H., Qian, Y.: Staggered discontinuous Galerkin methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 302, 251–266 (2015)
Chung, E., Cockburn, B., Fu, G.: The staggered DG method is the limit of a hybridizable DG method. Part II: The Stokes flow. J. Sci. Comput. 66(2), 870–887 (2016)
Chung, E., Lee, C.S.: A staggered discontinuous Galerkin method for the convection–diffusion equation. J. Numer. Math. 20(1), 1–31 (2012)
Chung, E.T., Engquist, B.: Optimal discontinuous Galerkin methods for wave propagation. SIAM J. Numer. Anal. 44(5), 2131–2158 (2006)
Chung, E.T., Engquist, B.: Optimal discontinuous Galerkin methods for the acoustic wave equation in higher dimensions. SIAM J. Numer. Anal. 47(5), 3820–3848 (2009)
Chung, E.T., Kim, H.H.: A deluxe FETI-DP algorithm for a hybrid staggered discontinuous Galerkin method for H(curl)-elliptic problems. Internat. J. Numer. Methods Eng. 98(1), 1–23 (2014)
Chung, E.T., Kim, H.H., Widlund, O.B.: Two-level overlapping Schwarz algorithms for a staggered discontinuous Galerkin method. SIAM J. Numer. Anal. 51(1), 47–67 (2013)
Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)
Cockburn, B., Shu, C.W.: The local discontinuous Galerkin method for time-dependent convection–diffusion systems. SIAM J. Numer. Anal. 35(6), 2440–2463 (1998)
Debussche, A., Printems, J.: Numerical simulation of the stochastic Korteweg–de Vries equation. Phys. D 134(2), 200–226 (1999)
Feng, B.F., Mitsui, T.: A finite difference method for the Korteweg–de Vries and the Kadomtsev–Petviashvili equations. J. Comput. Appl. Math. 90(1), 95–116 (1998)
Holmer, J.: The initial-boundary value problem for the Korteweg–de Vries equation. Commun. Partial Differ. Equ. 31(7–9), 1151–1190 (2006)
Kim, H.H., Chung, E.T., Lee, C.S.: A staggered discontinuous Galerkin method for the Stokes system. SIAM J. Numer. Anal. 51(6), 3327–3350 (2013)
Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. (5) 39(240), 422–443 (1895)
Lee, J.J., Kim, H.H.: Analysis of a staggered discontinuous Galerkin method for linear elasticity. J. Sci. Comput. 66(2), 625–649 (2016)
Levy, D., Shu, C.W., Yan, J.: Local discontinuous Galerkin methods for nonlinear dispersive equations. J. Comput. Phys. 196(2), 751–772 (2004)
Liu, H., Yan, J.: A local discontinuous Galerkin method for the Korteweg–de Vries equation with boundary effect. J. Comput. Phys. 215(1), 197–218 (2006)
Samii, A., Panda, N., Michoski, C., Dawson, C.: A hybridized discontinuous Galerkin method for the nonlinear Korteweg–de Vries equation. J. Sci. Comput. 68(1), 191–212 (2016)
Süli, E., Mayers, D.F.: An Introduction to Numerical Analysis. Cambridge University Press, Cambridge (2003)
Yan, J., Shu, C.W.: A local discontinuous Galerkin method for KdV type equations. SIAM J. Numer. Anal. 40(2), 769–791 (2002)
Acknowledgements
The authors would like to thank Prof. Sunmi Lee at Kyung Hee University for introducing KdV equations to the authors and suggesting development of staggered discontinuous Galerkin methods for the KdV equations.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors were supported by NRF-2015R1A5A1009350.
Rights and permissions
About this article
Cite this article
Yang, H.J., Kim, H.H. A Hybrid Staggered Discontinuous Galerkin Method for KdV Equations. J Sci Comput 77, 502–523 (2018). https://doi.org/10.1007/s10915-018-0714-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0714-x