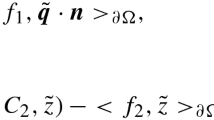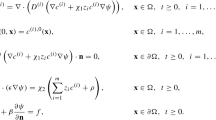Skip to main content
Springer Nature Link
Log in

A Linearized Local Conservative Mixed Finite Element Method for Poisson–Nernst–Planck Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

A Correction to this article was published on 21 June 2018

This article has been updated

Abstract

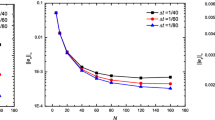
In this paper, a linearized local conservative mixed finite element method is proposed and analyzed for Poisson–Nernst–Planck (PNP) equations, where the mass fluxes and the potential flux are introduced as new vector-valued variables to equations of ionic concentrations (Nernst–Planck equations) and equation of the electrostatic potential (Poisson equation), respectively. These flux variables are crucial to PNP equations on determining the Debye layer and computing the electric current in an accurate fashion. The Raviart–Thomas mixed finite element is employed for the spatial discretization, while the backward Euler scheme with linearization is adopted for the temporal discretization and decoupling nonlinear terms, thus three linear equations are separately solved at each time step. The proposed method is more efficient in practice, and locally preserves the mass conservation. By deriving the boundedness of numerical solutions in certain strong norms, an unconditionally optimal error analysis is obtained for all six unknowns: the concentrations p and n, the mass fluxes \({{\varvec{J}}}_p=\nabla p + p {\varvec{\sigma }}\) and \({{\varvec{J}}}_n=\nabla n - n {\varvec{\sigma }}\), the potential \(\psi \) and the potential flux \({\varvec{\sigma }}= \nabla \psi \) in \(L^{\infty }(L^2)\) norm. Numerical experiments are carried out to demonstrate the efficiency and to validate the convergence theorem of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Change history

  • 21 June 2018

    The original version of this article contained a mistake. There are error in line breaks in Eqs. 4.3 and 4.4 and the word “quad” was included inadvertently in Eq. 4.4.

References

  1. Bochev, P., Lehoucq, R.: On the finite element solution of the pure Neumann problem. SIAM Rev. 47, 50–66 (2005)

    Article  MathSciNet  Google Scholar 

  2. Biler, P., Dolbeault, J.: Long time behavior of solutions of Nernst–Planck and Debye–Hückel drift–diffusion systems. Ann. Henri Poincaré 1, 461–472 (2000)

    Article  MathSciNet  Google Scholar 

  3. Biler, P., Hebisch, W., Nadzieja, T.: The Debye system: existence and large time behavior of solutions. Nonlinear Anal. 23, 1189–1209 (1994)

    Article  MathSciNet  Google Scholar 

  4. Brenner, S., Scott, L.: The Mathematical Theory of Finite Element Methods. Springer, New York (2002)

    Book  Google Scholar 

  5. Brera, M., Jerome, J., Mori, Y., Sacco, R.: A conservative and monotone mixed-hybridized finite element approximation of transport problems in heterogeneous domains. Comput. Methods Appl. Mech. Eng. 199, 2709–2770 (2010)

    Article  MathSciNet  Google Scholar 

  6. Brezzi, F., Marini, L., Micheletti, S., Pietra, P., Sacco, R., Wang, S.: Discretization of semiconductor device problems (I). Handb. Numer. Anal. XIII, 317–441 (2005)

    MathSciNet  MATH  Google Scholar 

  7. Brunk, M., Kværnø, A.: Positivity preserving discretization of time dependent semiconductor drift–diffusion equations. Appl. Numer. Math. 62, 1289–1301 (2012)

    Article  MathSciNet  Google Scholar 

  8. Cherrier, P., Milani, A.: Linear and Quasi-linear Evolution Equations in Hilbert Spaces. Grad. Stud. Math., vol. 135. AMS, Providence (2012)

    Book  Google Scholar 

  9. Demlow, A.: Suboptimal and optimal convergence in mixed finite element methods. SIAM J. Numer. Anal. 39, 1938–1953 (2002)

    Article  MathSciNet  Google Scholar 

  10. Dawson, C., Sun, S., Wheeler, M.: Compatible algorithm for coupled flow and transport. Comput. Methods Appl. Mech. Eng. 193, 2562–2580 (2004)

    MathSciNet  MATH  Google Scholar 

  11. Debye, P., Huckel, E.: Zur theorie der elektrolyte. Phys. Zeitschr. 24, 185–206 (1923)

    MATH  Google Scholar 

  12. Duran, R.: Error analysis in \(L^p,1\le p \le \infty \), for mixed finite element methods for linear and quasi-linear elliptic problems. RAIRO Model. Math. Anal. Numer. 22, 371–387 (1988)

    Article  MathSciNet  Google Scholar 

  13. Flavell, A., Machen, M., Eisenberg, R., Kabre, J., Liu, C., Li, X.: A conservative finite difference scheme for Poisson–Nernst–Planck equations. J. Comput. Electron. 15, 1–15 (2013)

    Google Scholar 

  14. Frank, F., Knabner, P.: Convergence analysis of a BDF2/mixed finite element discretization of a Darcy–Nernst–Planck–Poisson system. ESAIM M2AN 51, 1883–1902 (2017)

    Article  MathSciNet  Google Scholar 

  15. Frank, F., Ray, N., Knabner, P.: Numerical investigation of homogenized Stokes–Nernst–Planck–Poisson systems. Comput. Visual. Sci. 14, 385–400 (2011)

    Article  MathSciNet  Google Scholar 

  16. Gajewski, H., Gröger, K.: On the basic equations for carrier transport in semiconductors. J. Math. Anal. Appl. 113, 12–35 (1986)

    Article  MathSciNet  Google Scholar 

  17. Gao, H., He, D.: Linearized conservative finite element methods for the Nernst–Planck–Poisson equations. J. Sci. Comput. 72, 1269–1289 (2017)

    Article  MathSciNet  Google Scholar 

  18. Gao, H., Qiu, W.: Error analysis of mixed finite element methods for nonlinear parabolic equations. J. Sci. Comput. (2018). https://doi.org/10.1007/s10915-018-0643-8

    Article  Google Scholar 

  19. He, D., Pan, K.: An energy preserving finite difference scheme for the Poisson–Nernst–Planck system. Appl. Math. Comput. 287–288, 214–223 (2016)

    MathSciNet  Google Scholar 

  20. He, M., Sun, P.: Error analysis of mixed finite element method for Poisson–Nernst–Planck system. Numer. Methods Partial Differ. Equ. 33, 1924–1948 (2017)

    Article  MathSciNet  Google Scholar 

  21. He, M., Sun, P.: Mixed finite element analysis for the Poisson-Nernst-Planck/Stokes coupling. J. Comput. Appl. Math. 341, 61–79 (2018)

    Article  MathSciNet  Google Scholar 

  22. Heywood, J., Rannacher, R.: Finite element approximation of the nonstationary Navier–Stokes problem IV: error analysis for second-order time discretization. SIAM J. Numer. Anal. 27, 353–384 (1990)

    Article  MathSciNet  Google Scholar 

  23. Hou, Y., Li, B., Sun, W.: Error analysis of splitting Galerkin methods for heat and sweat transport in textile materials. SIAM J. Numer. Anal. 51, 88–111 (2013)

    Article  MathSciNet  Google Scholar 

  24. Johnson, C., Thomee, V.: Error estimates for some mixed finite element methods for parabolic type problems. RAIRO Anal. Numer. 15, 41–78 (1981)

    Article  MathSciNet  Google Scholar 

  25. Li, B., Lu, B., Wang, Z., McCammon, J.A.: Solutions to a reduced Poisson–Nernst–Planck system and determination of reaction rates. Physica A 389, 1329–1345 (2010)

    Article  Google Scholar 

  26. Liu, H., Wang, Z.: A free energy satisfying finite difference method for Poisson–Nernst–Planck equations. J. Comput. Phys. 268, 363–376 (2014)

    Article  MathSciNet  Google Scholar 

  27. Liu, Y., Shu, C.: Analysis of the local discontinuous Galerkin method for the drift–diffusion model of semiconductor devices. Sci. China Math. 59, 115–140 (2016)

    Article  MathSciNet  Google Scholar 

  28. Logg, A., Mardal, K., Wells, G. (eds.): Automated Solution of Differential Equations by the Finite Element Method. Springer, Berlin (2012)

    MATH  Google Scholar 

  29. Lu, B., Holst, M., McCammon, J., Zhou, Y.: Poisson–Nernst–Planck equations for simulating biomolecular diffusion–reaction processes I: finite element solutions. J. Comput. Phys. 229, 6979–6994 (2010)

    Article  MathSciNet  Google Scholar 

  30. Mauri, A., Bortolossi, A., Novielli, G., Sacco, R.: 3D finite element modeling and simulation of industrial semiconductor devices including impact ionization. J. Math. Ind. 5, 18 (2015). https://doi.org/10.1186/s13362-015-0015-z

    Article  MathSciNet  Google Scholar 

  31. Metti, M., Xu, J., Liu, C.: Energetically stable discretizations for charge transport and electrokinetic models. J. Comput. Phys. 306, 1–18 (2016)

    Article  MathSciNet  Google Scholar 

  32. Mirzadeh, M., Gibou, F.: A conservative discretization of the Poisson–Nernst–Planck equations on adaptive Cartesian grids. J. Comput. Phys. 274, 633–653 (2014)

    Article  MathSciNet  Google Scholar 

  33. Mock, M.: An initial value problem from semiconductor device theory. SIAM J. Math. Anal. 5, 597–612 (1974)

    Article  MathSciNet  Google Scholar 

  34. Naga, A., Zhang, Z.: The polynomial-preserving recovery for higher order finite element methods in 2D and 3D. Disc. Contin. Dyn. Syst. Ser. B 5, 769–798 (2005)

    Article  MathSciNet  Google Scholar 

  35. Prohl, A., Schmuck, M.: Convergent discretizations for the Nernst–Planck–Poisson system. Numer. Math. 111, 591–630 (2009)

    Article  MathSciNet  Google Scholar 

  36. Prohl, A., Schmuck, M.: Convergent finite element for discretizations of the Navier–Stokes–Nernst–Planck–Poisson system. M2AN Math. Model. Numer. Anal. 44, 531–571 (2010)

    Article  MathSciNet  Google Scholar 

  37. Scharfetter, D., Gummel, H.: Large signal analysis of a silicon read diode oscillator. IEEE Trans. Electron. Dev. 16, 64–77 (1969)

    Article  Google Scholar 

  38. Schmuck, M.: Analysis of the Navier–Stokes–Nernst–Planck–Poisson system. Math. Models Methods Appl. Sci. 19, 993–1015 (2009)

    Article  MathSciNet  Google Scholar 

  39. Sun, W., Sun, Z.: Finite difference methods for a nonlinear and strongly coupled heat and moisture transport system in textile materials. Numer. Math. 120, 153–187 (2012)

    Article  MathSciNet  Google Scholar 

  40. Sun, Y., Sun, P., Zheng, B., Lin, G.: Error analysis of finite element method for Poisson–Nernst–Planck equations. J. Comput. Appl. Math. 301, 28–43 (2016)

    Article  MathSciNet  Google Scholar 

  41. Thomee, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer, Berlin (2006)

    MATH  Google Scholar 

  42. Wei, G., Zheng, Q., Chen, Z., Xia, K.: Variational multiscale models for charge transport. SIAM Rev. 54, 699–754 (2012)

    Article  MathSciNet  Google Scholar 

  43. Xu, S., Chen, M., Majd, S., Yue, X., Liu, C.: Modeling and simulating asymmetrical conductance changes in Gramicidin pores. Mol. Based Math. Biol. 2, 34–55 (2014)

    Article  Google Scholar 

  44. Raviart, R., Thomas, J.: A mixed finite element method for 2nd order elliptic problems. In: Galligani, I., Magenes, E. (eds.) Mathematical Aspects of Finite Element Methods. Lecture Notes in Math, vol. 606. Springer, New York (1977)

    Google Scholar 

  45. Zheng, Q., Chen, D., Wei, G.: Second-order Poisson Nernst–Planck solver for ion channel transport. J. Comput. Phys. 230, 5239–5262 (2011)

    Article  MathSciNet  Google Scholar 

  46. Zienkiewicz, O., Zhu, J.: The superconvergence patch recovery and a posteriori error estimates, part I: the recovery technique. Int. J. Numer. Methods Eng. 33, 1331–1364 (1992)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, 430074, People’s Republic of China

    Huadong Gao

  2. Hubei Key Laboratory of Engineering Modeling and Scientific Computing, Huazhong University of Science and Technology, Wuhan, 430074, China

    Huadong Gao

  3. Department of Mathematical Sciences, University of Nevada Las Vegas, 4505 Maryland Parkway, Las Vegas, NV, 89154, USA

    Pengtao Sun

Authors
  1. Huadong Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Pengtao Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Pengtao Sun.

Additional information

The work of the first author was supported in part by the National Science Foundation of China No. 11501227 and Fundamental Research Funds for the Central Universities, HUST, P.R. China, under Grant Nos. 2014QNRC025, 2015QN13, and 2017KFYXJJ089. The work of the second author was partially supported by NSF Grant DMS-1418806.

The original version of this article was revised: The errors in Eqs. 4.3 and 4.4 have been corrected.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, H., Sun, P. A Linearized Local Conservative Mixed Finite Element Method for Poisson–Nernst–Planck Equations. J Sci Comput 77, 793–817 (2018). https://doi.org/10.1007/s10915-018-0727-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0727-5

Keywords

Mathematics Subject Classification