Abstract
In this paper, we formulate and analyze discontinuous Galerkin (DG) methods to solve several partial differential equations (PDEs) with high order spatial derivatives, including the heat equation, a third order wave equation, a fourth order equation and the linear Schrödinger equation in one dimension. Following the idea of local DG methods, we first rewrite each PDE into its first order form and then apply a general DG formulation. The numerical fluxes are introduced as linear combinations of average values of fluxes, and jumps of the solution as well as the auxiliary variables at cell interfaces. The main focus of the present work is to identify a sub-family of the numerical fluxes by choosing the coefficients in the linear combinations, so the solution and some auxiliary variables of the proposed DG methods are optimally accurate in the \(L^2\) norm. In our analysis, one key component is to design some special projection operator(s), tailored for each choice of numerical fluxes in the sub-family, to eliminate those terms at cell interfaces that would otherwise contribute to the sub-optimality of the error estimates. Our theoretical findings are validated by a set of numerical examples.
Similar content being viewed by others
References
Bassi, F., Rebay, S.: A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier–Stokes equations. J. Comput. Phys. 131(2), 267–279 (1997)
Baumann, C.E., Oden, J.T.: A discontinuous \(hp\) finite element method for convection–diffusion problems. Comput. Methods Appl. Mech. Eng. 175(3–4), 311–341 (1999)
Benjamin, T.B., Bona, J.L., Mahony, J.J.: Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 272(1220), 47–78 (1972)
Bialynicki-Birula, I., Mycielski, J.: Gaussons: solitons of the logarithmic Schrödinger equation. Phys. Scr. 20(3–4), 539 (1979)
Bona, J., Chen, H., Karakashian, O., Xing, Y.: Conservative, discontinuous Galerkin methods for the generalized Korteweg-de Vries equation. Math. Comput. 82(283), 1401–1432 (2013)
Castillo, P., Cockburn, B., Schötzau, D., Schwab, C.: Optimal a priori error estimates for the \(hp\)-version of the local discontinuous Galerkin method for convection-diffusion problems. Math. Comput. 71(238), 455–478 (2002)
Chen, Y., Cockburn, B., Dong, B.: A new discontinuous Galerkin method, conserving the discrete \(H^2\)-norm, for third-order linear equations in one space dimension. IMA J. Numer. Anal. 36(4), 1570–1598 (2016)
Chen, Y., Cockburn, B., Dong, B.: Superconvergent HDG methods for linear, stationary, third-order equations in one-space dimension. Math. Comput. 85(302), 2715–2742 (2016)
Cheng, Y., Chou, C.-S., Li, F., Xing, Y.: \(L^{2}\) stable discontinuous Galerkin methods for one-dimensional two-way wave equations. Math. Comput. 86(303), 121–155 (2017)
Cheng, Y., Shu, C.-W.: A discontinuous Galerkin finite element method for time dependent partial differential equations with higher order derivatives. Math. Comput. 77(262), 699–730 (2008)
Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)
Cockburn, B., Hou, S., Shu, C.-W.: The Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV. The multidimensional case. Math. Comput. 54(190), 545–581 (1990)
Cockburn, B., Lin, S.-Y., Shu, C.-W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one-dimensional systems. J. Comput. Phys. 84(1), 90–113 (1989)
Cockburn, B., Shu, C.-W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework. Math. Comput. 52(186), 411–435 (1989)
Cockburn, B., Shu, C.-W.: The Runge-Kutta local projection \(P^1\)-discontinuous-Galerkin finite element method for scalar conservation laws. ESAIM Math. Model. Numer. Anal. 25(3), 337–361 (1991)
Cockburn, B., Shu, C.-W.: The local discontinuous Galerkin method for time-dependent convection–diffusion systems. SIAM J. Numer. Anal. 35(6), 2440–2463 (1998)
Cockburn, B., Shu, C.-W.: The Runge–Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys. 141(2), 199–224 (1998)
Cowan, S., Enns, R., Rangnekar, S., Sanghera, S.S.: Quasi-soliton and other behaviour of the nonlinear cubic-quintic Schrödinger equation. Can. J. Phys. 64(3), 311–315 (1986)
Dong, B.: Optimally convergent HDG method for third-order Korteweg-de Vries type equations. J. Sci. Comput. 73(2–3), 712–735 (2017)
Dong, B., Shu, C.-W.: Analysis of a local discontinuous Galerkin method for linear time-dependent fourth-order problems. SIAM J. Numer. Anal. 47(5), 3240–3268 (2009)
Douglas, J., Dupont, T.: Interior penalty procedures for elliptic and parabolic Galerkin methods. In: Glowinski, R., Lions, J.L. (eds.) Computing Methods in Applied Sciences, pp. 207–216. Springer, Berlin, Heidelberg (1976)
Dutt, A., Greengard, L., Rokhlin, V.: Spectral deferred correction methods for ordinary differential equations. BIT Numer. Math. 40(2), 241–266 (2000)
Ji, L., Xu, Y.: Optimal error estimates of the local discontinuous Galerkin method for Willmore flow of graphs on Cartesian meshes. Int. J. Numer. Anal. Model. 8(2), 252–283 (2011)
Li, B.Q.: Discontinuous Finite Elements in Fluid Dynamics and Heat Transfer. Springer, London (2006)
Liu, H., Yan, J.: The direct discontinuous Galerkin (DDG) methods for diffusion problems. SIAM J. Nume. Anal. 47(1), 675–698 (2008)
Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Tech. Report LA-UR-73-479, Los Alamos Scientific Laboratory (1973)
Shu, C.-W.: Discontinuous Galerkin methods: general approach and stability. In: Bertoluzza, S., Falletta, S., Russo, G., Shu, C.-W. (eds.) Numerical solutions of partial differential equations, pp. 149–201. Birkhäuser, Basel (2009)
Xia, Y., Xu, Y., Shu, C.: Efficient time discretization for local discontinuous Galerkin methods. Discrete Contin. Dyn. Syst. Seri. B 8(3), 677 (2007)
Xu, Y., Shu, C.-W.: Local discontinuous Galerkin methods for nonlinear Schrödinger equations. J. Comput. Phys. 205(1), 72–97 (2005)
Xu, Y., Shu, C.-W.: Optimal error estimates of the semidiscrete local discontinuous Galerkin methods for high order wave equations. SIAM J. Numer. Anal. 50(1), 79–104 (2012)
Yan, J., Shu, C.-W.: A local discontinuous Galerkin method for KdV type equations. SIAM J. Numer. Anal. 40(2), 769–791 (2002)
Yan, J., Shu, C.-W.: Local discontinuous Galerkin methods for partial differential equations with higher order derivatives. J. Sci. Comput. 17(1–4), 27–47 (2002)
Author information
Authors and Affiliations
Corresponding author
Additional information
Y. Cheng: Research is supported by NSF Grants DMS-1453661 and DMS-1720023. F. Li: Research is supported in part by NSF Grant DMS-1719942. Y. Xu: Research is supported by NSFC Grant No.11722112 and 91630207.
Appendices
A The Proof of Theorem 4.3
In this appendix, we prove the \(L^2\) stability of the DG scheme (4.6)–(4.7) with the numerical fluxes (4.5) and \(\alpha =\frac{1}{2},\beta _1=\beta _2=0\), namely
Five energy equations will be derived first.
\(\bullet \)The first energy equation. With \(\alpha =\frac{1}{2},\beta _1=\beta _2=0\), the first energy equation (4.9) becomes
\(\bullet \)The second energy equation. We take the test functions \(v=-\frac{1}{2}(q_h)_t\), \(w=\frac{1}{2}p_h\) and \(z=0\) in (4.10), use the definition of \(F_p\), \(F_q\) and \(F_u\) in (A.1), and obtain
\(\bullet \)The third energy equation. With \(\alpha =\frac{1}{2},\beta _1=\beta _2=0\), (4.14) becomes
\(\bullet \)The fourth energy equation. Here we take the test functions \(v=-p_h\), \(w=(u_h)_t\) and \(z=q_h\) in (4.15), use the definition of \(F_p\), \(F_q\) and \(F_u\) in (A.1), and obtain
\(\bullet \)The fifth energy equation. We take the time derivative of (4.15) and get
With the test functions in (A.6) taken as \(v=-(p_h)_t\), \(w=(u_h)_{tt}\) and \(z=(q_h)_t\), using the definition of \(F_p\), \(F_q\) and \(F_u\) in (A.1), we have
\(\bullet \)Proof of Theorem4.3
Proof
We sum up the energy equations (A.2)–(A.5) and (A.7), and get
Thus, we have
We integrate (A.9) with respect to time over [0, T], and obtain
From the third energy equation (A.4) and the fifth energy equation (A.7), we have
Therefore, we can obtain the \(L^2\) stability in Theorem 4.3. \(\square \)
B The Derivation of the Conditions (4.18)
In this appendix, we will give the derivation of the conditions (4.18) that are to ensure the matrices \(S_1\) and \(S_2\) in (4.22) to be positive semi-definite. For this, we use the following sufficient and necessary condition for an \(n\times n \) matrix to be positive semi-definite: all the principal minors\(D_k\)are nonnegative, \(k=1, \ldots n\). Here, \(D_k\) is formed by deleting any\(n-k\) rows and the corresponding columns. Additionally, we require the relation \(\alpha ^2+\beta _1\beta _2=\frac{1}{4}\), which helps with simplifying the conditions and is also needed for optimal accuracy.
For the matrix \(S_1\), the first principal minors are
the second principal minors are
and the third principal minor is
Let the first principal minors be nonnegative, we have \(\beta _1\le 0\) and \(\beta _2\le 0\). From the second principal minors being nonnegative, we obtain
Let the third principal minor \(D_3\) be nonnegative, with \(\beta _1\le 0\) and the assumption \(\alpha ^2+\beta _1\beta _2=\frac{1}{4}\), we get
We observe that, with \(\beta _1\beta _2\ge 0\), the inequality (B.5) will automatically ensure the first inequality in (B.4). Combining all we have so far, the following conditions are derived to ensure \(S_1\) be positive semi-definite
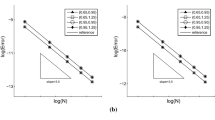
The region of \(\beta _1,\beta _2\) in the condition (4.18) for the stability. Left: \(\alpha =-\sqrt{\frac{1}{4}-\beta _1\beta _2}\); Right: \(\alpha =-\frac{1}{4}\)
For the matrix \(S_2\), we follow the similar analysis as for \(S_1\). By requiring all the first and the second principal minors being nonnegative, we get
Let the third order principal minor of \(S_2\) be nonnegative, also with \(\beta _2\ge 0\), we obtain
Using \(\beta _2\le 0\) and assuming \(\beta _1\le 0\), one can see that (B.9) implies the first inequality in (B.8), which on the other hand ensures the first inequality in (B.7). Combining (B.7)–(B.9) with \(\alpha ^2+\beta _1\beta _2=\frac{1}{4}\), we have the conditions for \(S_2\) as
Finally, we reach the conditions in (4.18) by putting (B.6) and (B.10) together. To get some idea about these conditions in (4.18), we present two plots in Fig. 1. In the left figure, we plot those pairs \((\beta _1,\beta _2)\) such that with the respective \(\alpha =-\sqrt{\frac{1}{4}-\beta _1\beta _2}\), the conditions in (4.18) are all satisfied. In the right figure, we fix \(\alpha =-\frac{1}{4}\), and plot \((\beta _1,\beta _2)\) satisfying the conditions in (4.18). Note that such \((\beta _1,\beta _2)\) form part of the parabola: \(\beta _1\beta _2=\frac{1}{4}-\alpha ^2=\frac{3}{16}\), see the solid line in red.
Rights and permissions
About this article
Cite this article
Fu, P., Cheng, Y., Li, F. et al. Discontinuous Galerkin Methods with Optimal \(L^2\) Accuracy for One Dimensional Linear PDEs with High Order Spatial Derivatives. J Sci Comput 78, 816–863 (2019). https://doi.org/10.1007/s10915-018-0788-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0788-5