Abstract
Based on the kernel-free boundary integral method proposed by Ying and Henriquez (J Comput Phys 227(2):1046–1074, 2007), which is a second-order accurate method for general elliptic partial differential equations, this work develops it to be a fourth-order accurate version for the modified Helmholtz equation. The updated method is in line with the original one. Unlike the traditional boundary integral method, it does not need to know any analytical expression of the fundamental solution or Green’s function in evaluation of boundary or volume integrals. Boundary value problems under consideration are reformulated into Fredholm boundary integral equations of the second kind, whose corresponding discrete forms are solved with the simplest Krylov subspace iterative method, the Richardson iteration. During each iteration, a Cartesian grid based nine-point compact difference scheme is used to discretize the simple interface problem whose solution is the boundary or volume integral in the BIEs. The resulting linear system is solved by a fast Fourier transform based solver, whose computational work is roughly proportional to the number of grid nodes in the Cartesian grid used. As the discrete boundary integral equations are well-conditioned, the iteration converges within an essentially fixed number of steps, independent of the mesh parameter. Numerical results are presented to verify the solution accuracy and demonstrate the algorithm efficiency.











Similar content being viewed by others
References
Atkinson, K.E.: The Numerical Solution of Integral Equations of the Second Kind. Cambridge University Press, Cambridge (1997)
Ben Avraham, D., Fokas, A.S.: The solution of the modified Helmholtz equation in a wedge and an application to diffusion-limited coalescence. Phys. Lett. A 263(4–6), 355–359 (1999)
Bakker, M.: Modeling groundwater flow to elliptical lakes and through multi-aquifer elliptical inhomogeneities. Adv. Water Resour. 27(5), 497–506 (2004)
Bakker, M., Kuhlman, K.L.: Computational issues and applications of line-elements to model subsurface flow governed by the modified Helmholtz equation. Adv. Water Resour. 34(9), 1186–1194 (2011)
Banerjee, P.K., Butterfield, R.: Boundary Element Methods in Engineering Science, vol. 17. McGraw-Hill, London (1981)
Barnes, J., Hut, P.: A hierarchical O(N log N) force-calculation algorithm. Nature 324(6096), 446 (1986)
Barnes, J.E.: A modified tree code: Don’t laugh. It runs. J. Comput. Phys. 87(1), 161–170 (1990)
Bazant, M.Z., Thornton, K., Ajdari, A.: Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 70(2), 021506 (2004)
Beale, J.T., Layton, A.T.: On the accuracy of finite difference methods for elliptic problems with interfaces. Commun. Appl. Math. Comput. Sci. 1(1), 91–119 (2006)
Brebbia, C., Dominguez, J.: Boundary element methods for potential problems. Appl. Math. Model. 1(7), 372–378 (1977)
Chapko, R., Kress, R.: Rothe’s method for the heat equation and boundary integral equations. J. Integral Equ. Appl. 9, 47–69 (1997)
Cheng, H., Crutchfield, W.Y., Gimbutas, Z., Greengard, L.F., Ethridge, J.F., Huang, J., Rokhlin, V., Yarvin, N., Zhao, J.: A wideband fast multipole method for the Helmholtz equation in three dimensions. J. Comput. Phys. 216(1), 300–325 (2006)
Cheng, H., Greengard, L., Rokhlin, V.: A fast adaptive multipole algorithm in three dimensions. J. Comput. Phys. 155(2), 468–498 (1999)
Cheng, H., Huang, J., Leiterman, T.J.: An adaptive fast solver for the modified Helmholtz equation in two dimensions. J. Comput. Phys. 211(2), 616–637 (2006)
Di Gioia, A.: Fast multipole accelerated boundary element techniques for large-scale problems, with applications to MEMS. Ph.D. thesis, Università di Trento. Dipartimento di ingegneria meccanica e strutturale (2005)
Fedkiw, R.P., Aslam, T., Merriman, B., Osher, S.: A non-oscillatory eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 152(2), 457–492 (1999)
Feng, H., Barua, A., Li, S., Li, X.: A parallel adaptive treecode algorithm for evolution of elastically stressed solids. Commun. Comput. Phys. 15(2), 365–387 (2014)
Gibou, F., Fedkiw, R., Cheng, L.T., Kang, M.: A second order accurate symmetric discretization of the Poisson equation on irregular domains. J. Comput. Phys. 176, 205–227 (2002)
Gibou, F., Fedkiw, R.P.: A fourth order accurate discretization for the Laplace and heat equations on arbitrary domains, with applications to the Stefan problem. J. Comput. Phys. 202, 577–601 (2005)
Greengard, L., Huang, J., Rokhlin, V., Wandzura, S.: Accelerating fast multipole methods for the Helmholtz equation at low frequencies. IEEE Comput. Sci. Eng. 5(3), 32–38 (1998)
Greengard, L., Kropinski, M.C.: An integral equation approach to the incompressible Navier–Stokes equations in two dimensions. SIAM J. Sci. Comput. 20(1), 318–336 (1998)
Greengard, L., Rokhlin, V.: A fast algorithm for particle simulations. J. Comput. Phys. 73(2), 325–348 (1987)
Greengard, L., Rokhlin, V.: A new version of the fast multipole method for the Laplace equation in three dimensions. Acta Numer. 6, 229–269 (1997)
Hackbusch, W.: Integral Equations, Theory and Numerical Treatment. Birkhäuser, Basel (1995)
Hackbusch, W., Nowak, Z.P.: On the fast matrix multiplication in the boundary element method by panel clustering. Numer. Math. 54(4), 463–491 (1989)
He, X., Lin, T., Lin, Y.: Immersed finite element methods for elliptic interface problems with non-homogeneous jump conditions. Int. J. Numer. Anal. Model. 8(2), 284–301 (2011)
Hewett, D.W.: The embedded curved boundary method for orthogonal simulation meshes. J. Comput. Phys. 138(2), 585–616 (1997)
Hou, S., Liu, X.D.: A numerical method for solving variable coefficient elliptic equation with interfaces. J. Comput. Phys. 202, 411–445 (2005)
Houstis, E.N., Papatheodorou, T.S.: Algorithm 543: FFT9, fast solution of Helmholtz-type partial differential equations D3. ACM Trans. Math. Softw. 5(4), 490–493 (1979)
Houstis, E.N., Papatheodorou, T.S.: High-order fast elliptic equation solver. ACM Trans. Math. Softw. 5(4), 431–441 (1979)
Hsiao, G.C., Wendland, W.L.: Boundary Integral Equations. Springer, Berlin (2008)
Jaswon, M.: Integral equation methods in potential theory. I. In: Proceedings of the Royal Society of London A, vol. 275, pp. 23–32. The Royal Society (1963)
Johansen, H., Colella, P.: A Cartesian grid embedded boundary method for Poisson’s equation on irregular domains. J. Comput. Phys. 147(1), 60–85 (1998)
Kropinski, M.C.A., Quaife, B.D.: Fast integral equation methods for Rothe’s method applied to the isotropic heat equation. Comput. Math. Appl. 61(9), 2436–2446 (2011)
Kropinski, M.C.A., Quaife, B.D.: Fast integral equation methods for the modified Helmholtz equation. J. Comput. Phys. 230(2), 425–434 (2011)
Kuhlman, K.L., Neuman, S.P.: Laplace-transform analytic-element method for transient porous-media flow. J. Eng. Math. 64(2), 113 (2009)
Le, D.V., Khoo, B.C., Peraire, J.: An immersed interface method for viscous incompressible flows involving rigid and flexible boundaries. J. Comput. Phys. 220(1), 109–138 (2006)
Leveque, R.J., Li, Z.: The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 31(4), 1019–1044 (1994)
Li, H., Huang, J.: High accuracy solutions of the modified Helmholtz equation. In: Information Technology and Intelligent Transportation Systems, pp. 29–37. Springer (2017)
Li, Z.: A fast iterative algorithm for elliptic interface problems. SIAM J. Numer. Anal. 35(1), 230–254 (1998)
Li, Z., Ito, K.: The Immersed Interface Method: Numerical Solutions of PDEs Involving Interfaces and Irregular Domains, vol. 33. SIAM, Philadelphia (2006)
Lindsay, K., Krasny, R.A.: A particle method and adaptive treecode for vortex sheet motion in three-dimensional flow. J. Comput. Phys. 172(2), 879–907 (2001)
Liu, Y., Nishimura, N.: The fast multipole boundary element method for potential problems: a tutorial. Eng. Anal. Bound. Elem. 30(5), 371–381 (2006)
Marques, A.N., Nave, J.C., Rosales, R.R.: A correction function method for Poisson problems with interface jump conditions. J. Comput. Phys. 230, 7567–7597 (2011)
Marques, A.N., Nave, J.C., Rosales, R.R.: High order solution of Poisson problems with piecewise constant coefficients and interface jumps. J. Comput. Phys. 335, 497–515 (2017)
Mayo, A.: The fast solution of Poisson’s and the biharmonic equations on irregular regions. SIAM J. Numer. Anal. 21(2), 285–299 (1984)
Mayo, A.: Fast high order accurate solution of Laplace’s equation on irregular regions. SIAM J. Sci. Stat. Comput. 6(1), 144–157 (1985)
Mayo, A.: The rapid evaluation of volume integrals of potential theory on general regions. J. Comput. Phys. 100(2), 236–245 (1992)
Peskin, C.S.: The immersed boundary method. Acta Numer. 11, 479–517 (2002)
Phillips, J.R., White, J.K.: A precorrected-FFT method for electrostatic analysis of complicated 3-D structures. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 16(10), 1059–1072 (1997)
Politis, C.G., Papalexandris, M.V., Athanassoulis, G.A.: A boundary integral equation method for oblique water-wave scattering by cylinders governed by the modified helmholtz equation. Appl. Ocean Res. 24(4), 215–233 (2002)
Quaife, B.D.: Fast integral equation methods for the modified Helmholtz equation. Ph.D. thesis, Science: Department of Mathematics (2011)
Rokhlin, V.: Rapid solution of integral equations of classical potential theory. J. Comput. Phys. 60(2), 187–207 (1985)
Rosser, J.B.: Nine-point difference solutions for Poisson’s equation. Comput. Math. Appl. 1(3–4), 351–360 (1975)
Saad, Y., Schultz, M.H.: GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7(3), 856–869 (1986)
Samarskii, A.A.: The Theory of Difference Schemes, vol. 240. CRC Press, London (2001)
Sauter, S., Schwab, C.: Boundary Element Methods. Springer, Berlin (2010)
Steinbach, O.: Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements. Springer, Berlin (2007)
Strack, O.D.: Groundwater Mechanics. Prentice Hall, Englewood Cliffs (1989)
Ying, L., Biros, G., Zorin, D.: A kernel-independent adaptive fast multipole algorithm in two and three space dimensions. J. Comput. Phys. 196, 591–626 (2004)
Ying, L., Biros, G., Zorin, D.: A high-order 3D boundary integral equation solver for elliptic PDEs in smooth domains. J. Comput. Phys. 219, 247–275 (2006)
Ying, W., Henriquez, C.S.: A kernel-free boundary integral method for elliptic boundary value problems. J. Comput. Phys. 227(2), 1046–1074 (2007)
Ying, W., Wang, W.C.: A kernel-free boundary integral method for implicitly defined surfaces. J. Comput. Phys. 252, 606–624 (2013)
Ying, W., Wang, W.C.: A kernel-free boundary integral method for variable coefficients elliptic PDEs. Commun. Comput. Phys. 15(4), 1108–1140 (2014)
Zhou, Y.C., Zhao, S., Feig, M., Wei, G.W.: High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources. J. Comput. Phys. 213(1), 1–30 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised: The errors in the equations, texts and references have been corrected.
Research of the second author was supported in part by the National Science Foundation of the USA under Grant DMS 0915023, and is supported by the National Natural Science Foundation of China under Grants DMS 91330203, DMS 11101278, DMS 91130012 and DMS 11771290. Research of the second author was also supported by the Young Thousand Talents Program of China.
Appendix: Calculation for Jumps of Partial Derivatives
Appendix: Calculation for Jumps of Partial Derivatives
Jumps of partial derivatives of the solution to the interface problem (22) are needed not just in the correction for the finite difference equations but also in the extraction of boundary data from the discrete finite difference solutions.
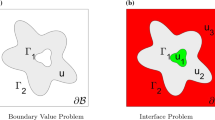
Let \(u(\mathbf{x})\) be a piecewise smooth function defined in \({\mathcal B}\), whose normal derivative \(u_{\mathbf{n}}\) as well as u itself may be discontinuous across the interface. Computation of jumps for u on \(\varGamma \) starts from the interface problem (22), which is reiterated below
Let s be the arc length parameter of the curve \(\varGamma \), \(\mathbf{t} = (x'(s), y'(s))^\mathrm{T}\) be the unit tangent vector, \(\mathbf{n} = (y'(s), -x'(s))^\mathrm{T} = \mathbf{t}^{\perp }\) be the unit outward normal vector on \(\varGamma \). Suppose that \(\varphi = \varphi (s)\) and \(\psi = \psi (s)\) are two sufficiently smooth functions defined on \(\varGamma \).
Differentiating (41) with respect to the arc length parameter s, together with (42), we get
Solving this two by two linear system gives us jumps of the first-order partial derivatives of u on \(\varGamma \).
Differentiating the identities in (43) with respect to the arc length parameter s, respectively, together with the modified Helmholtz equation (40), we get
Solving this three by three linear system gives us jumps of the second-order partial derivatives of u on \(\varGamma \).
Differentiating the first equation in (44) with respect to the arc length parameter s gives us
with
Differentiating the second equation in (44) with respect to the arc length parameter s gives us
with
We may get two more equations for jumps of the third-order partial derivatives by first differentiating the modified Helmholtz equation and then taking jumps of the resulting equations across \(\varGamma \). They read
We may get jumps of the third-order partial derivatives, \([u_{xxx}]\), \([u_{xxy}]\), \([u_{xyy}]\) and \([u_{yyy}]\), by solving the system consisting of Eqs. (45)–(48).
Differentiating (45) with respect to the arc length parameter s yields
with
Differentiating (46) with respect to the arc length parameter s leads to
with
Other three equations for jumps of the fourth-order partial derivatives read
which are similarly obtained by first differentiating the modified Helmholtz equation and then taking jumps of the resulting equations across \(\varGamma \).
We may get jumps of the fourth-order partial derivatives, \([u_{xxxx}]\), \([u_{xxxy}]\), \([u_{xxyy}]\), \([u_{xyyy}]\) and \([u_{yyyy}]\), by solving the system consisting of Eqs. (49)–(53).
Rights and permissions
About this article
Cite this article
Xie, Y., Ying, W. A Fourth-Order Kernel-Free Boundary Integral Method for the Modified Helmholtz Equation. J Sci Comput 78, 1632–1658 (2019). https://doi.org/10.1007/s10915-018-0821-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0821-8