Abstract
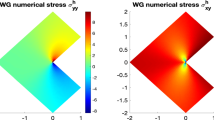
This paper investigates lowest-order weak Galerkin finite element methods for solving linear elasticity problems on rectangular and brick meshes. Specifically, constant vectors are used in element interiors and on element interfaces respectively for approximating displacement. For these constant basis functions, their discrete weak gradients are calculated in the local Raviart–Thomas spaces \( RT_{[0]}^d \) (\( d=2 \) or 3), whereas their discrete weak divergences are calculated as elementwise constants. Discrete weak strains are calculated accordingly. Then these quantities are used to develop finite element schemes in both strain-div and grad-div formulations, on both rectangular and brick meshes. A theoretical analysis supported by numerical experiments in both 2-dim and 3-dim reveal that the methods are locking-free and have optimal 1st order convergence in displacement, stress, and dilation (divergence of displacement), when the exact solution has full regularity. The methods can also capture low-regularity solutions very well. Strategies for efficient implementation including Schur complement are presented. Extension to quadrilateral and hexahedral meshes, in both theoretical analysis and numerical experiments, is also examined.




Similar content being viewed by others
References
Alberty, J., Carstensen, C., Funken, S., Klose, R.: Matlab implementation of the finite element method in elasticity. Computing 69, 239–263 (2002)
Arnold, D., Awanou, G., Qiu, W.: Mixed finite elements for elasticity on quadrilateral meshes. Adv. Comput. Math. 41, 553–572 (2015)
Arnold, D., Boffi, D., Falk, R.: Approximation by quadrilateral finite elements. Math. Comput. 71, 909–922 (2002)
Brenner, S., Sung, L.-Y.: Linear finite element methods for planar linear elasticity. Math. Comput. 59, 321–338 (1992)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 15, Third edn. Springer, New York (2008)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer, Berlin (1991)
Carstensen, C., Schedensack, M.: Medius analysis and comparison results for first-order finite element methods in linear elasticity. IMA J. Numer. Anal. 35, 1591–1621 (2015)
Hu, J., Man, H., Wang, J., Zhang, S.: The simplest nonconforming mixed finite element method for linear elasticity in the symmetric formulation on n-rectangular grids. Comput. Math. Appl. 71, 1317–1336 (2016)
Kozlov, V.A., Maz’ya, V.G., Rossmann, J.: Spectral Problems Associated with Corner Singularities of Solutions to Elliptic Equations. Mathematical Surveys and Monographs, vol. 85. American Mathematical Society, Providence (2001)
Lamichhane, B.P.: A mixed finite element method for nearly incompressible elasticity and Stokes equations using primal and dual meshes with quadrilateral and hexahedral grids. J. Comput. Appl. Math. 260, 356–363 (2014)
Lamichhane, B.P., Stephan, E.P.: A symmetric mixed finite element method for nearly incompressible elasticity based on biorthogonal systems. Numer. Methods PDEs 28, 1336–1353 (2012)
Lawrence Livermore National Laboratory. VisIt User’s Manual, 1.5 edition (2005)
Li, H., Nistor, V.: LNG FEM: graded meshes on domains of polygonal structures. Contemp. Math. 586, 239–246 (2013)
Liu, J., Cali, R.: A note on the approximation properties of the locally divergence-free finite elements. Int. J. Numer. Anal. Model. 5, 693–703 (2008)
Liu, J., Tavener, S., Wang, Z.: The lowest order weak Galerkin finite element methods for the Darcy equation on quadrilateral and hybrid meshes. J. Comput. Phys. 359, 312–330 (2018)
Mao, S., Chen, S.: A quadrilateral nonconforming finite element for linear elasticity problem. Adv. Comput. Math. 28, 81–100 (2008)
Mijuca, D.: On hexahedral finite element hc8/27 in elasticity. Comput. Mech. 33, 466–480 (2004)
Wang, C., Wang, J., Wang, R., Zhang, R.: A locking-free weak Galerkin finite element method for elasticity problems in the primal formulation. J. Comput. Appl. Math. 307, 346–366 (2016)
Wang, J., Ye, X.: A weak Galerkin finite element method for second order elliptic problems. J. Comput. Appl. Math. 241, 103–115 (2013)
Wheeler, M., Xue, G., Yotov, I.: A multipoint flux mixed finite element method on distorted quadrilaterals and hexahedra. Numer. Math. 121, 165–204 (2012)
Yi, S.-Y.: Nonconforming mixed finite element methods for linear elasticity using rectangular elements in two and three dimensions. Calcolo 42, 115–133 (2005)
Yi, S.-Y.: A new nonconforming mixed finite element method for linear elasticity. Math. Models Methods Appl. Sci. 16, 979–999 (2006)
Zhang, S.: On the nested refinement of quadrilateral and hexahedral finite elements and the affine approximation. Numer. Math. 98, 559–579 (2004)
Zhang, Z.: Analysis of some quadrilateral nonconforming elements for incompressible elasticity. SIAM J. Numer. Anal. 34, 640–663 (1997)
Author information
Authors and Affiliations
Corresponding author
Additional information
G. Harper was partially supported by US National Science Foundation (NSF) MSGI for 2017 summer internship at Pacific Northwest National Lab and NSF under Grants DMS-1419077 and DMS-1819252. J. Liu was partially supported by NSF under Grants DMS-1419077 and and DMS-1819252. S. Tavener was partially supported by NSF under Grant DMS-1720473.
Rights and permissions
About this article
Cite this article
Harper, G., Liu, J., Tavener, S. et al. Lowest-Order Weak Galerkin Finite Element Methods for Linear Elasticity on Rectangular and Brick Meshes. J Sci Comput 78, 1917–1941 (2019). https://doi.org/10.1007/s10915-018-0837-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0837-0