Skip to main content
SpringerLink
Log in

Finite Element Method for Two-Sided Fractional Differential Equations with Variable Coefficients: Galerkin Approach

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

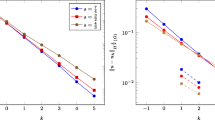
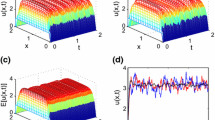
This paper develops a Galerkin approach for two-sided fractional differential equations with variable coefficients. By the product rule, we transform the problem into an equivalent formulation which additionally introduces the fractional low-order term. We prove the existence and uniqueness of the solutions of the Dirichlet problems of the equations with certain diffusion coefficients. We adopt the Galerkin formulation, and prove its error estimates. Finally, several numerical examples are provided to illustrate the fidelity and accuracy of the proposed theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Adams, R.A., Fournier, J.F.: Sobolev Spaces. Academic Press, New York (2003)

    MATH  Google Scholar 

  2. Benson, D.A., Tadjeran, C., Meerschaert, M.M., Farnham, I., Pohll, G.: Radial fractional-order dispersion through fractured rock. Water Resour. Res. 40, 1–9 (2004)

    Article  Google Scholar 

  3. Benson, D.A., Schumer, R., Meerschaert, M.M., Wheatcraft, S.W.: Fractional dispersion, Levy motion, and the made tracer tests. Transp. Porous Media 42, 211–240 (2001)

    Article  MathSciNet  Google Scholar 

  4. Brenner, S., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Springer, New York (1994)

    Book  MATH  Google Scholar 

  5. Carreras, B.A., Lynch, V.E., Zaslavsky, G.M.: Anomalous diffusion and exit time distribution of particle travers in plasma turbulence models. Phys. Plasma 8, 5096–5103 (2001)

    Article  Google Scholar 

  6. Chen, M.H., Deng, W.H.: Fourth order accurate scheme for the space fractional diffusion equatioins. SIAM J. Numer. Anal. 52(3), 1418–1438 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  7. De Nápoli, P.L., Drelichman, I.: Elementary proofs of embedding theorems for potential spaces of radial functions. In: Ruzhansky, M., Tikhonov, S. (eds.) Methods of Fourier Analysis and Approximation Theory. Applied and Numerical Harmonic Analysis, pp. 115–138. Birkhauser, Cham (2016)

    Chapter  Google Scholar 

  8. Ervin, V.J., Roop, J.P.: Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Equ. 22(3), 558–576 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ervin, V.J., Heuer, N., Roop, J.P.: Numerical approximation of a time dependent, nonlinear, space-fractional diffusion equation. SIAM J. Numer. Anal. 45, 572–591 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ervin, V.J., Heuer, N., Roop, J.P.: Regularity of the solution to 1-D fractional order diffusion equations. Math. Comput. 87, 2273–2294 (2016). https://doi.org/10.1090/mcom/3295

    Article  MathSciNet  MATH  Google Scholar 

  11. Hao, Z., Sun, Z., Cao, W.: A fourth-order approximation of fractional derivatives with its applications. J. Comput. Phys. 281, 787–805 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hilfer, R.: Applications of Fractional Calculus in Physics. Word Scientific, Singapore (2000)

    Book  MATH  Google Scholar 

  13. Kirchner, J.W., Feng, X., Neal, C.: Fractal stream chemistry and its implications for containant transport in catchments. Nature 403, 524–526 (2000)

    Article  Google Scholar 

  14. Li, X., Xu, C.: The existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation. Commun. Comput. Phys. 8, 1016–1051 (2010)

    MathSciNet  MATH  Google Scholar 

  15. Liu, F., Anh, V., Turner, I.: Numerical solution of the space fractional Fokker–Planck equation. J. Comput. Appl. Math. 166, 209–219 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  16. Magin, R.L.: Fractional Calculus in Bioengineering. Begell House Publishers, Danbury (2006)

    Google Scholar 

  17. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Phys. 172, 65–77 (2004)

    MathSciNet  MATH  Google Scholar 

  18. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56, 80–90 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  19. Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)

    MATH  Google Scholar 

  20. Sabatelli, L., Keating, S., Dudley, J., Richmond, P.: Waiting time distributions in financial markets. Eur. Phys. J. B 27, 273–27 (2002)

    MathSciNet  Google Scholar 

  21. Samko, S.G., Kilbas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science Publishers, Yverdon (1993)

    MATH  Google Scholar 

  22. Schumer, R., Benson, D.A., Meerschaert, M.M., Wheatcraft, S.W.: Eulerian derivation of the fractional advection–dispersion equation. J. Contam. Hydrol. 48(1), 69–88 (2001)

    Article  Google Scholar 

  23. Shlesinger, M.F., West, B.J., Klafter, J.: Levy dynamics of enhanced diffusion: application to turbulence. Phys. Rev. Lett. 58, 1100–1103 (1987)

    Article  MathSciNet  Google Scholar 

  24. Tadjeran, C., Meerschaert, M.M., Scheffler, H.-P.: A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 213(1), 205–213 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  25. Wang, H., Yang, D.: Wellposedness of variable-coefficient conservative fractional elliptic differential equations. SIAM J. Numer. Anal. 51(2), 1088–1107 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang, H., Basu, T.S.: A fast finite difference method for two-dimensional space-fractional diffusion equations. SIAM J. Sci. Comput. 34, A2444–A2458 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  27. Wang, H., Wang, K.: An \(O(N \log ^2 N)\) alternating-direction finite difference method for two-dimensional fractional diffusion equations. J. Comput. Phys. 230, 7830–7839 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang, H., Yang, D., Zhu, S.: A Petrov–Galerkin finite element method for variable-coefficient fractional diffusion equations. Comput. Methods Appl. Mech. Eng. 290, 45–56 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wang, H., Yang, D., Zhu, S.: Accuracy of finite element methods for boundary-value problems of steady-state fractional diffusion equations. J. Sci. Comput. 70, 429–449 (2017). https://doi.org/10.1007/s10915-016-0196-7

    Article  MathSciNet  MATH  Google Scholar 

  30. Xu, Q., Hesthaven, J.S.: Discontinuous Galerkin method for fractional convection diffusion equations. SIAM J. Numer. Anal. 52, 405–423 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  31. Yang, D.P., Wang, H.: Wellposedness and regularity of steady-state two-sided variable-coefficient conservative space-fractional diffusion equations (2016). arXiv:1606.04912 [math.NA]

  32. Zaslavsky, G.M., Stevens, D., Weitzner, H.: Self-similar transport in incomplete chaos. Phys. Rev. E 48, 1683–1694 (1993)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Hao would like to acknowledge the support by National Natural Science Foundation of China (No. 11671083), China Scholarship Council (No. 201506090065). Lin gratefully acknowledges the support from National Science Foundation (DMS-1555072, DMS-1736364, and DMS-1821233). Cai would like to acknowledge the support by the NSF Grant DMS-1522707.

Author information

Authors and Affiliations

  1. Department of Mathematics, Southeast University, Nanjing, 210096, People’s Republic of China

    Zhaopeng Hao

  2. Department of Mathematics and Statistics, Oakland University, Rochester, MI, 48309, USA

    Moongyu Park

  3. Department of Mathematics, Purdue University, West Lafayette, IN, 47907, USA

    Guang Lin & Zhiqiang Cai

  4. School of Mechanical Engineering, Purdue University, West Lafayette, IN, 47907, USA

    Guang Lin

Authors
  1. Zhaopeng Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Moongyu Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guang Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhiqiang Cai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Moongyu Park.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hao, Z., Park, M., Lin, G. et al. Finite Element Method for Two-Sided Fractional Differential Equations with Variable Coefficients: Galerkin Approach. J Sci Comput 79, 700–717 (2019). https://doi.org/10.1007/s10915-018-0869-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0869-5

Keywords

Mathematics Subject Classification

Search

Navigation