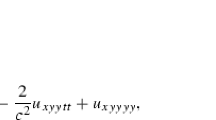Abstract
We construct a family of compact fourth order accurate finite difference schemes for the three dimensional scalar wave (d’Alembert) equation with constant or variable propagation speed. High order accuracy is of key importance for the numerical simulation of waves as it reduces the dispersion error (i.e., the pollution effect). The schemes that we propose are built on a stencil that has only three nodes in any coordinate direction or in time, which eliminates the need for auxiliary initial or boundary conditions. These schemes are implicit in time and conditionally stable. A particular scheme with the maximum Courant number can be chosen within the proposed class. The inversion at the upper time level is done by FFT for constant coefficients and multigrid for variable coefficients, which keeps the overall complexity of time marching comparable to that of a typical explicit scheme.











Similar content being viewed by others
References
Abide, S., Binous, M.S., Zeghmati, B.: An efficient parallel high-order compact scheme for the 3D incompressible Navier–Stokes equations. Int. J. Comput. Fluid Dyn. 31(4–5), 214–229 (2017). https://doi.org/10.1080/10618562.2017.1326592
Babuška, I.M., Sauter, S.A.: Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers? SIAM Rev. 42(3), 451–484 (electronic) (2000). Reprint of SIAM J. Numer. Anal. 34 (1997), no. 6, 2392–2423 [MR1480387 (99b:65135)]
Bayliss, A., Goldstein, C.I., Turkel, E.: On accuracy conditions for the numerical computation of waves. J. Comput. Phys. 59(3), 396–404 (1985)
Bérenger, J.P.: Perfectly Matched Layer (PML) for Computational Electromagnetics. Synthesis Lectures on Computational Electromagnetics. Morgan and Claypool Publishers, San Rafael, CA (2007)
Brandt, A.: Rigorous quantitative analysis of multigrid. I. Constant coefficients two-level cycle with \(L_2\)-norm. SIAM J. Numer. Anal. 31(6), 1695–1730 (1994). https://doi.org/10.1137/0731087
Briggs, W.L., Henson, V.E., McCormick, S.F.: A Multigrid Tutorial, 2nd edn. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2000)
Britt, S., Tsynkov, S., Turkel, E.: A compact fourth order scheme for the Helmholtz equation in polar coordinates. J. Sci. Comput. 45(1–3), 26–47 (2010). https://doi.org/10.1007/s10915-010-9348-3
Britt, S., Tsynkov, S., Turkel, E.: Numerical simulation of time-harmonic waves in inhomogeneous media using compact high order schemes. Commun. Comput. Phys. 9(3), 520–541 (2011)
Britt, S., Tsynkov, S., Turkel, E.: A high order compact time/space finite difference scheme for the wave equation with variable speed of sound. J. Sci. Comput. 76, 777–811 (2018). https://doi.org/10.1007/s10915-017-0639-9
Britt, S., Tsynkov, S., Turkel, E.: Numerical solution of the wave equation with variable wave speed on nonconforming domains by high-order difference potentials. J. Comput. Phys. 354, 26–42 (2018)
Chabassier, J., Imperiale, S.: Introduction and study of fourth order theta schemes for linear wave equations. J. Comput. Appl. Math. 245, 194–212 (2013). https://doi.org/10.1016/j.cam.2012.12.023
Deraemaeker, A., Babuška, I.M., Bouillard, P.: Dispersion and pollution of the FEM solution for the Helmholtz equation in one, two and three dimensions. Int. J. Numer. Methods Eng. 46, 471–499 (1999)
Fishelov, D.: A new fourth-order compact scheme for the Navier–Stokes equations in irregular domains. Comput. Math. Appl. 74(1), 6–25 (2017). https://doi.org/10.1016/j.camwa.2016.10.020
Fu, Y.: Compact fourth-order finite difference schemes for Helmholtz equation with high wave numbers. J. Comput. Math. 26(1), 98–111 (2008)
Grote, M.J., Sim, I.: Efficient PML for the wave equation (2010). arXiv:1001.0319
Harari, I., Turkel, E.: Accurate finite difference methods for time-harmonic wave propagation. J. Comput. Phys. 119(2), 252–270 (1995)
Hocking, L.R., Greif, C.: Closed-form multigrid smoothing factors for lexicographic Gauss–Seidel. IMA J. Numer. Anal. 32(3), 795–812 (2012). https://doi.org/10.1093/imanum/drr037
Liang, H., Liu, M.Z., Lv, W.: Stability of \(\theta \)-schemes in the numerical solution of a partial differential equation with piecewise continuous arguments. Appl. Math. Lett. 23(2), 198–206 (2010). https://doi.org/10.1016/j.aml.2009.09.012
Lončarić, J., Tsynkov, S.V.: Optimization of acoustic source strength in the problems of active noise control. SIAM J. Appl. Math. 63(4), 1141–1183 (2003)
Ma, Y., Yu, J., Wang, Y.: An efficient complex-frequency shifted-perfectly matched layer for second-order acoustic wave equation. Int. J. Numer. Methods Eng. 97(2), 130–148 (2014). https://doi.org/10.1002/nme.4594
Ma, Y., Yu, J., Wang, Y.: A novel unsplit perfectly matched layer for the second-order acoustic wave equation. Ultrasonics 54(6), 1568–1574 (2014). https://doi.org/10.1016/j.ultras.2014.03.016
Petropavlovsky, S., Tsynkov, S., Turkel, E.: A method of boundary equations for unsteady hyperbolic problems in 3D. J. Comput. Phys. 365, 294–323 (2018). https://doi.org/10.1016/j.jcp.2018.03.039
Ryaben’kii, V.S.: Method of Difference Potentials and Its Applications, Springer Series in Computational Mathematics, vol. 30. Springer, Berlin (2002)
Saad, Y.: Iterative Methods for Sparse Linear Systems, 2nd edn. Society for Industrial and Applied Mathematics, Philadelphia (2003). https://doi.org/10.1137/1.9780898718003
Singer, I., Turkel, E.: High-order finite difference methods for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 163(1–4), 343–358 (1998)
Singer, I., Turkel, E.: High-order finite difference methods for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 163(1–4), 343–358 (1998). https://doi.org/10.1016/S0045-7825(98)00023-1
Trottenberg, U., Oosterlee, C.W., Schüller, A.: Multigrid. Academic Press Inc., San Diego (2001). With contributions by A. Brandt, P. Oswald and K. Stüben
Turkel, E., Gordon, D., Gordon, R., Tsynkov, S.: Compact 2D and 3D sixth order schemes for the Helmholtz equation with variable wave number. J. Comput. Phys. 232(1), 272–287 (2013). https://doi.org/10.1016/j.jcp.2012.08.016
Zhou, L., Armfield, S.: A compact fourth-order spatial discretisation applied to the Navier–Stokes equations. ANZIAM Journal 56, 481–501 (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
We dedicate this paper to the memory of Professor Saul (Shalom) Abarbanel who provided mentorship and inspiration to a whole generation of students and colleagues.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Work supported by the US Army Research Office (ARO) under Grant No. W911NF-16-1-0115 and the US–Israel Binational Science Foundation (BSF) under Grant No. 2014048.
Rights and permissions
About this article
Cite this article
Smith, F., Tsynkov, S. & Turkel, E. Compact High Order Accurate Schemes for the Three Dimensional Wave Equation. J Sci Comput 81, 1181–1209 (2019). https://doi.org/10.1007/s10915-019-00970-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-019-00970-x
Keywords
- Unsteady wave propagation
- Fourth order accurate approximation
- Small stencil
- Cartesian grid
- Implicit scheme
- Multigrid methods