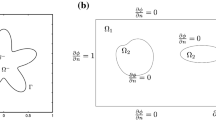
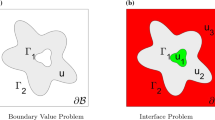
Abstract
This work proposes second-order and fourth-order versions of a Cartesian grid based kernel-free boundary integral (KFBI) method for the biharmonic equation on both bounded irregular domains and singly periodic irregular domains. It is further development of the previous KFBI method for second-order elliptic PDEs. It reformulates boundary value problems of the fourth-order PDE as boundary integral equations of the first kind but the solution never needs to know the fundamental solution or Green’s function of the elliptic operator. Evaluation of boundary or volume integrals in the solution of boundary integral equations is made by solving equivalent interface problems on Cartesian grids with standard finite difference methods and fast Fourier transform based solvers. The work decomposes the biharmonic equation into two Poisson equations. It assumes the solution to one Poisson equation, which has no boundary conditions, as the sum of a volume integral with a double layer boundary integral, and applies Green’s third identity to derive a scalar boundary integral equation from the other Poisson equation that are subject to two boundary conditions. In the solution of the scalar boundary integral equation, each volume or boundary integral is evaluated with the KFBI method. Numerical examples are presented to demonstrate the solution accuracy and algorithm efficiency. A remarkable point of the work is that the nine-point compact difference scheme in dealing with each split second-order elliptic interface problem on irregular domains yields fourth-order accurate solution for the biharmonic equation.






Similar content being viewed by others
References
Adini, A., Clough, R.W.: Analysis of Plate Bending by the Finite Element Method. University of California, Berkeley (1960)
Arad, M., Yakhot, A., Ben-Dor, G.: A highly accurate numerical solution of a biharmonic equation. Numer. Methods Partial Differ. Equ. 13(4), 375–391 (1997)
Argyris, J.H., Dunne, P.C.: The finite element method applied to fluid dynamics. In: Hewitt, B.L., Illingworth, C.R., Lock, R.C., Mangler, K.W., McDonnel, J.H., Richards, C., Walkden, F. (eds.) Computational Methods and Problems in Aeronautical Fluid Dynamics, pp. 158–197. Academic Press, London (1976)
Baker, G.A.: Finite element methods for elliptic equations using nonconforming elements. Math. Comput. 31, 45–59 (1977)
Bhargava, R.: Solution of a biharmonic equation. Nature 201(4918), 530 (1964)
Bialecki, B., Karageorghis, A.: Spectral chebyshev collocation for the Poisson and biharmonic equations. SIAM J. Sci. Comput. 32(5), 2995–3019 (2010)
Bjørstad, P.: Fast numerical solution of the biharmonic Dirichlet problem on rectangles. SIAM J. Numer. Anal. 20(1), 59–71 (1983)
Brebbia, C.A., Telles, J.C.F., Wrobel, L.C.: Boundary Element Techniques: Theory and Applications in Engineering. Springer, New York (2012)
Brenner, S., Sung, L.: C0 interior penalty methods for fourth order elliptic boundary value problems on polygonal domains. J. Sci. Comput. 22/23(1–3), 83–118 (2005)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer, Berlin (1991)
Buzbee, B.L., Golub, G.H., Nielson, C.W.: On direct methods for solving Poisson’s equations. SIAM J. Numer. Anal. 7(4), 627–656 (1970)
Camp, C.V.: Solution of the nonhomogeneous biharmonic equation by the boundary element method. Ph.D. thesis, Oklahoma State University (1987)
Chan, R.H., DeLillo, T.K., Horn, M.A.: The numerical solution of the biharmonic equation by conformal mapping. SIAM J. Sci. Comput. 18(6), 1571–1582 (1997)
Chen, G., Li, Z., Lin, P.: A fast finite difference method for biharmonic equations on irregular domains and its application to an incompressible Stokes flow. Adv. Comput. Math. 29(2), 113–133 (2008)
Chen, J.T., Wu, C.S., Lee, Y.T., Chen, K.H.: On the equivalence of the Trefftz method and method of fundamental solutions for Laplace and biharmonic equations. Comput. Math. Appl. 53, 851–879 (2007)
Cheng, X.L., Han, W., Huang, H.C.: Some mixed finite element methods for biharmonic equation. J. Comput. Appl. Math. 126, 91–109 (2000)
Christiansen, S.: Integral equations without a unique solution can be made useful for solving some plane harmonic problems. IMA J. Appl. Math. 16(2), 143–159 (1975)
Christiansen, S.: Derivation and analytical investigation of three direct boundary integral equations for the fundamental biharmonic problem. J. Comput. Appl. Math. 91(2), 231–247 (1998)
Christiansen, S., Hougaard, P.: An investigation of a pair of integral equations for the biharmonic problem. IMA J. Appl. Math. 22(1), 15–27 (1978)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978)
Ciarlet, P.G., Raviart, P.A.: A mixed finite element method for the biharmonic equation. In: Mathematical Aspects of Finite Elements in Partial Differential Equations, pp. 125–145 (1974)
Cockburn, B., Dong, B., Guzmán, J.: A hybridizable and superconvergent discontinuous Galerkin method for biharmonic problems. J. Sci. Comput. 40(1–3), 141–187 (2009)
Collatz, L.: The Numerical Treatment of Differential Equations, vol. 60. Springer, New York (2012)
Conte, S.D., Dames, R.T.: An alternating direction method for solving the biharmonic equation. Math. Tables Other Aids Comput. 12(63), 198–205 (1958)
Costabel, M., Lusikka, I., Saranen, J.: Comparison of three boundary element approaches for the solution of the clamped plate problem. In: Ciarlet, P.G., Lions, J.L. (eds.) Boundary Elements IX, vol. 2, pp. 19–34. Springer, Berlin (1987)
Costabel, M., Saranen, J.: Boundary element analysis of a direct method for the biharmonic Dirichlet problem. In: The Gohberg anniversary collection, pp. 569–587 (1989)
Davini, C., Pitacco, I.: An unconstrained mixed method for the biharmonic problem. SIAM J. Numer. Anal. 38(3), 820–836 (2000)
Ehrlich, L.W.: Solving the biharmonic equation as coupled finite difference equations. SIAM J. Numer. Anal. 8(2), 278–287 (1971)
Ehrlich, L.W., Gupta, M.M.: Some difference schemes for the biharmonic equation. SIAM J. Numer. Anal. 12(5), 773–790 (1975)
Fairweather, G., Gourlay, A., Mitchell, A.: Some high accuracy difference schemes with a splitting operator for equations of parabolic and elliptic type. Numer. Math. 10(1), 56–66 (1967)
Fairweather, G., Karageorghis, A.: The method of fundamental solutions for elliptic boundary value problems. Adv. Comput. Math. 9(1–2), 69 (1998)
Fornberg, B.: A pseudospectral approach for polar and spherical geometries. SIAM J. Sci. Comput. 16(5), 1071–1081 (1995)
Fuglede, B.: On a direct method of integral equations for solving the biharmonic Dirichlet problem. Zeitschrift für Angewandte Mathematik und Mechanik 61(9), 449–459 (1981)
Glowinski, R., Pironneau, O.: Numerical methods for the first biharmonic equation and for the two-dimensional Stokes problem. SIAM Rev. 21(2), 167–212 (1979)
Greenbaum, A., Greengard, L., Mayo, A.: On the numerical solution of the biharmonic equation in the plane. Physica D 60, 216–225 (1992)
Greengard, L., Kropinski, M.C.: An integral equation approach to the incompressible Navier–Stokes equations in two dimensions. SIAM J. Sci. Comput. 20(1), 318–336 (1998)
Hadjidimos, A.: The numerical solution of a model problem biharmonic equation by using extrapolated alternating direction implicit methods. Numer. Math. 17(4), 301–317 (1971)
Heinrichs, W.: A stabilized treatment of the biharmonic operator with spectral methods. SIAM J. Sci. Stat. Comput. 12(5), 1162–1172 (1991)
Hockney, R.W.: A fast direct solution of Poisson’s equation using fourier analysis. JACM 12(1), 95–113 (1965)
Hsiao, G.C., Wendland, W.L.: Boundary Integral Equations. Springer, New York (2008)
Huang, S., Liu, Y.: A fast multipole boundary element method for solving the thin plate bending problem. Eng. Anal. Bound. Elem. 37(6), 967–976 (2013)
Huang, W., Tang, T.: Pseudospectral solutions for steady motion of a viscous fluid inside a circular boundary. Appl. Numer. Math. 33(1–4), 167–173 (2000)
Jaswon, M., Maiti, M.: An integral equation formulation of plate bending problems. J. Eng. Math. 2(1), 83–93 (1968)
Jaswon, M.A., Symm, G.T.: Integral Equation Methods in Potential Theory and Elastostatics, vol. 132. Academic Press, London (1977)
Jeon, Y.: An indirect boundary integral equation method for the biharmonic equation. SIAM J. Numer. Anal. 31(2), 461–476 (1994)
Jeon, Y.: New boundary element formulas for the biharmonic equation. Adv. Comput. Math. 9(1–2), 97–115 (1998)
Jeon, Y.: New indirect scalar boundary integral equation formulas for the biharmonic equation. J. Comput. Appl. Math. 135(2), 313–324 (2001)
Jeon, Y., McLean, W.: A new boundary element method for the biharmonic equation with Dirichlet boundary conditions. Adv. Comput. Math. 19(4), 339–354 (2003)
Jiang, S., Ren, R., Tsuji, P., Ying, L.: Second kind integral equations for the first kind Dirichlet problem of the biharmonic equation in three dimensions. J. Comput. Phys. 230(19), 7488–7501 (2011)
Jiang, Y., Wang, B., Xu, Y.: A fast Fourier–Galerkin method solving a boundary integral equation for the biharmonic equation. SIAM J. Numer. Anal. 52(5), 2530–2554 (2014)
Karageorghis, A.: Modified methods of fundamental solutions for harmonic and biharmonic problems with boundary singularities. Numer. Methods Partial Differ. Equ. 8(1), 1–19 (1992)
Karageorghis, A., Fairweather, G.: The method of fundamental solutions for the numerical solution of the biharmonic equation. J. Comput. Phys. 69(2), 434–459 (1987)
Karageorghis, A., Fairweather, G.: The Almansi method of fundamental solutions for solving biharmonic problems. Int. J. Numer. Methods Eng. 26(7), 1665–1682 (1988)
Karageorghis, A., Fairweather, G.: The simple layer potential method of fundamental solutions for certain biharmonic problems. Int. J. Numer. Methods Fluids 9(10), 1221–1234 (1989)
Katsikadelis, J., Massalas, C., Tzivanidis, G.: An integral equation of the plane problem of the theory of elasticity. Mech. Res. Commun. 4(3), 199–208 (1977)
Katsikadelis, J.T.: Boundary Elements: Theory and Applications. Elsevier, Amsterdam (2002)
Kupradze, V.D.: A method for the approximate solution of limiting problems in mathematical physics. USSR Comput. Math. Math. Phys. 4(6), 199–205 (1964)
Lai, M.C., Liu, H.C.: Fast direct solver for the biharmonic equation on a disk and its application to incompressible flows. Appl. Math. Comput. 164(3), 679–695 (2005)
Lascaux, P., Lesaint, P.: Some nonconforming finite elements for the plate bending problem (Revue francaise d’automatique, informatique, recherche opérationnelle). Analyse numérique 9(R1), 9–53 (1975)
Li, Z.: A fast iterative algorithm for elliptic interface problems. SIAM J. Numer. Anal. 35(1), 230–254 (1998). Please confirm the paper title for the reference [59]
Li, Z.C., Lee, M.G., Chiang, J.Y., Liu, Y.P.: The Trefftz method using fundamental solutions for biharmonic equations. J. Comput. Appl. Math. 235(15), 4350–4367 (2011)
Maiti, M., Chakrabarty, S.: Integral equation solutions for simply supported polygonal plates. Int. J. Eng. Sci. 12(10), 793–806 (1974)
Mayo, A.: The fast solution of Poisson’s and the biharmonic equations on irregular regions. SIAM J. Numer. Anal. 21(2), 285–299 (1984)
Morley, L.S.D.: The triangular equilibrium element in the solution of plate bending problems. Aeronat. Q. 19, 149–169 (1968)
Mu, L., Wang, J., Wang, Y., Ye, X.: A weak Galerkin mixed finite element method for biharmonic equations. In: Numerical Solution of Partial Differential Equations: Theory, Algorithms, and Their Applications, pp. 247–277. Springer, New York (2013)
Mu, L., Wang, J., Ye, X.: Weak Galerkin finite element methods for the biharmonic equation on polytopal meshes. Numer. Methods Partial Differ. Equ. 30(3), 1003–1029 (2014)
Poullikkas, A., Karageorghis, A., Georgiou, G.: Methods of fundamental solutions for harmonic and biharmonic boundary value problems. Comput. Mech. 21(4–5), 416–423 (1998)
Rim, K., Henry, A.S.: An Integral Equation Method in Plane Elasticity, vol. 779. National Aeronautics and Space Administration, Washington (1967)
Roache, P.J.: Computational Fluid Dynamics. Hermosa Publishers, Albuquerque (1976)
Roberts, J., Thomas, J.M.: Mixed and hybrid methods. In: Ciarlet, P.G., Lions, J.L. (eds.) Handbook of Numerical Analysis, vol. 2. North-Holland, Amsterdam (1991)
Rosser, J.B.: Nine-point difference solutions for Poisson’s equation. Comput. Math. Appl. 1(3–4), 351–360 (1975)
Saad, Y., Schultz, M.H.: GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7(3), 856–869 (1986)
Sakakibara, K.: Method of fundamental solutions for biharmonic equation based on Almansi-type decomposition. Appl. Math. 62(4), 297–317 (2017)
Samarskii, A.A.: The Theory of Difference Schemes, vol. 240. CRC Press, Boca Raton (2001)
Sokolnikoff, I.S.: Mathematical Theory of Elasticity. McGraw-Hill Book Company, New York (1956)
Steinbach, O.: Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements. Springer, New York (2007)
Stephenson, J.: Single cell discretizations of order two and four for biharmonic problems. J. Comput. Phys. 55(1), 65–80 (1984)
Süli, E., Mozolevski, I.: hp-Version interior penalty DGFEMs for the biharmonic equation. Comput. Methods Appl. Mech. Eng. 196(13–16), 1851–1863 (2007)
Timoshenko, S., Woinowsky-Krieger, S.: Theory of Plates and Shells, 2nd edn. McGraw-Hill, New York (1987)
Wong, Y.S., Jiang, H.: Approximate polynomial preconditioning applied to biharmonic equations. J. Supercomput. 3, 125–145 (1989)
Xie, Y., Ying, W.: A fourth-order kernel-free boundary integral method for the modified Helmholtz equation. J. Sci. Comput. (2018). https://doi.org/10.1007/s10915-018-0821-8
Ying, W.: A Cartesian grid-based boundary integral method for an elliptic interface problem on closely packed cells. Commun. Comput. Phys. 24(4), 1196–1220 (2018)
Ying, W., Henriquez, C.S.: A kernel-free boundary integral method for elliptic boundary value problems. J. Comput. Phys. 227(2), 1046–1074 (2007)
Ying, W., Wang, W.C.: A kernel-free boundary integral method for implicitly defined surfaces. J. Comput. Phys. 252, 606–624 (2013)
Ying, W., Wang, W.C.: A kernel-free boundary integral method for variable coefficients elliptic PDEs. Commun. Comput. Phys. 15(4), 1108–1140 (2014)
Zhang, R., Zhai, Q.: A weak Galerkin finite element scheme for the biharmonic equations by using polynomials of reduced order. J. Sci. Comput. 64(2), 559–585 (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research of the second author is supported by the Science Challenge Project of China under Grant No. TZ2016002 and the National Natural Science Foundation of China under Grant DMS-11771290. Research of the second author was also supported by the Young Thousand Talents Program of China.
Rights and permissions
About this article
Cite this article
Xie, Y., Ying, W. & Wang, WC. A High-Order Kernel-Free Boundary Integral Method for the Biharmonic Equation on Irregular Domains. J Sci Comput 80, 1681–1699 (2019). https://doi.org/10.1007/s10915-019-01000-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-019-01000-6