Skip to main content
Springer Nature Link
Log in

A New Numerical Method for an Asymptotic Coupled Model of Fractured Media Aquifer System

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

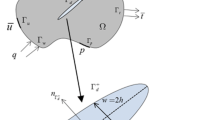
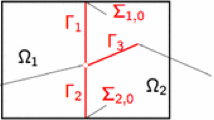
An asymptotic model coupling three-dimensional and two-dimensional equations is considered to demonstrate the flow in fractured media aquifer system in this paper. The flow is governed by Darcy’s law both in fractures and surrounding porous media. A new anisotropic and nonconforming finite element is constructed to solve the three-dimensional Darcy equation. The existence and uniqueness of the coupled solutions are deduced. Optimal error estimates are obtained in \(L^2\) and \(H^1\) norms. Numerical experiments show the accuracy and efficiency of the presented method. With the same number of nodal points and the same amount of computational costs, the results obtained by using the new element are much better than those by both \(Q_{1}\) conforming element and Wilson nonconforming element on the same meshes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Bauer, S., Liedl, R., Sauter, M.: Modeling of karst aquifer genesis: influence of exchange flow. Water Resour. Res. 39(10), 371–375 (2003)

    Article  Google Scholar 

  2. Bauer, S., Liedl, R., Sauter, M., Stauffer, F., Kinzelbach, W., Kovar, K., Hoehn, E.: Modelling of karst development considering conduit-matrix exchange flow. In: Calibration and Reliability in Groundwater Modelling: Coping with Uncertainty. Proceedings of the ModelCARE’99 Conference Held in Zurich, Switzerland, 20–23 Sept 1999 (2000)

  3. Birk, S., Liedl, R., Sauter, M., Teutsch, G.: Hydraulic boundary conditions as a controlling factor in karst genesis: a numerical modeling study on artesian conduit development in gypsum. Water Resour. Res. 39(1), SBH 2-1–SBH 2-14 (2003)

  4. Espinosa-Paredes, G., Morales-Zárate, E., Vázquez-Rodríguez, A.: Analytical analysis for mass transfer in a fractured porous medium. Pet. Sci. Technol. 31(19), 2004–2012 (2013)

    Article  Google Scholar 

  5. Cao, Y., Fei, H., Wang, X.: Analysis and finite element approximation of a coupled, continuum pipe-flow/Darcy model for flow in porous media with embedded conduits. Numer. Methods Partial Differ. Equ. 27(5), 1242–1252 (2011)

    Article  MathSciNet  Google Scholar 

  6. Chen, N., Gunzburger, M., Hu, B., Wang, X., Woodruff, C.: Calibrating the exchange coefficient in the modified coupled continuum pipe-flow model for flows in karst aquifers. J. Hydrol. 414–415(2), 294–301 (2012)

    Article  Google Scholar 

  7. Liu, W., Zhao, Q., Li, X., Li, J.: Anisotropic wilson element with conforming finite element approximation for a coupled continuum pipe-flow/Darcy model in karst aquifers. Math. Methods Appl. Sci. 38(17), 4024–4037 (2015)

    Article  MathSciNet  Google Scholar 

  8. Liu, W., Kang, Z., Rui, H.: Finite volume element approximation of the coupled continuum pipe-flow/Darcy model for flows in karst aquifers. Numer. Methods Partial Differ. Equ. 30(2), 376–392 (2014)

    Article  MathSciNet  Google Scholar 

  9. Liu, W., Cui, J., Xin, J.: A block-centered finite difference method for an unsteady asymptotic coupled model in fractured media aquifer system. J. Comput. Appl. Math. 337, 319–340 (2018)

    Article  MathSciNet  Google Scholar 

  10. Wang, X.: On the coupled continuum pipe flow model (CCPF) for flows in karst aquifer. Discrete Contin. Dyn. Syst. Ser. B 13(2), 489–501 (2009)

    MathSciNet  MATH  Google Scholar 

  11. Chen, Z., An, K., Liu, Y., Chen, W.: Adjoint method for an inverse problem of CCPF model. Chin. Ann. Math. 3(3), 337–354 (2014)

    Article  MathSciNet  Google Scholar 

  12. Liedl, R., Sauter, M., Hückinghaus, D., Clemens, T., Teutsch, G.: Simulation of the development of karst aquifers using a coupled continuum pipe flow model. Water Resour. Res. 39(3), 597–676 (2003)

    Article  Google Scholar 

  13. Wu, X., Kügler, P., Lu, S.: Identification of the exchange coefficient from indirect data for a coupled continuum pipe-flow model. Chin. Ann. Math. 35(3), 483–500 (2014)

    Article  MathSciNet  Google Scholar 

  14. Martin, V., Jaffré, J., Roberts, J.E.: Modeling fractures and barriers as interfaces for flow in porous media. SIAM J. Sci. Comput. 26(5), 1667–1691 (2005)

    Article  MathSciNet  Google Scholar 

  15. Hoang, T.-T.-P., Japhet, C., Kern, M., Roberts, J.E.: Space-time domain decomposition for reduced fracture models in mixed formulation. SIAM J. Numer. Anal. 54(1), 288–316 (2016)

    Article  MathSciNet  Google Scholar 

  16. Loper, D.E.: An analytic benchmark test for karst-aquifer flow. Geophys. Astrophys. Fluid Dyn. 107(5), 587–602 (2013)

    Article  MathSciNet  Google Scholar 

  17. Yao, B., Wei, J., Wang, D., Ma, D., Chen, Z.: Numerical study on seepage property of karst collapse columns under particle migration. CMES Comput. Model. Eng. Sci. 91(2), 81–100 (2013)

    MathSciNet  MATH  Google Scholar 

  18. Lesinigo, M., DAngelo, C., Quarteroni, A.: A multiscale Darcy–Brinkman model for fluid flow in fractured porous media. Numer. Math. 117(4), 717–752 (2011)

    Article  MathSciNet  Google Scholar 

  19. Angot, P., Boyer, F., Hubert, F.: Asymptotic and numerical modelling of flows in fractured porous media. ESAIM Math. Model. Numer. Anal. 43(2), 239–275 (2009)

    Article  MathSciNet  Google Scholar 

  20. Frih, N., Martin, V., Roberts, J.E., Saâda, A.: Modeling fractures as interfaces with nonmatching grids. Comput. Geosci. 16(4), 1043–1060 (2012)

    Article  Google Scholar 

  21. Tunc, X., Faille, I., Gallouët, T., Cacas, M.C., Havé, P.: A model for conductive faults with non-matching grids. Comput. Geosci. 16(2), 277–296 (2012)

    Article  Google Scholar 

  22. Morales, F., Showalter, R.E.: The narrow fracture approximation by channeled flow. J. Math. Anal. Appl. 365(1), 320–331 (2010)

    Article  MathSciNet  Google Scholar 

  23. Shi, D., Chen, S.: A class of nonconforming arbitrary quadrilateral elements. Numer. Math. A J. Chin. Univ. 2, 231–238 (1996)

    MATH  Google Scholar 

  24. Shi, Z.C., Chen, S.C.: Analysis of a nine degree plate bending element of Shecht. Chin. J. Numer. Math. Appl. 4, 73–79 (1989)

    Google Scholar 

  25. Shi, Z.C., Jiang, B., Xue, W.: A new superconvergence property of Wilson nonconforming finite element. Numer. Math. 78(2), 259–268 (1997)

    Article  MathSciNet  Google Scholar 

  26. Wilson, E.L., Taylor, R.L., Doherty, W.P., Ghaboussi, J.: Incompatible Displacement Models. Numerical and Computer Methods in Structural Mechanics, pp. 43–57. Academic Press, New York (1973)

    Google Scholar 

  27. Ciarlet, P.G., Lions, J.L.: Handbook of Numerical Analysis. Gulf Professional Publishing (Distributors for the United States), Amsterdam (1990)

    Google Scholar 

  28. Shi, Z.C.: A convergence condition for the quadrilateral Wilson element. Numer. Math. 44(3), 349–361 (1984)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics Science, Ludong University, Yantai, 264025, China

    Wei Liu

  2. Department of Applied Mathematics, The Hong Kong Polytechnic University, Hung Hom, Hong Kong

    Jintao Cui

  3. The Hong Kong Polytechnic University Shenzhen Research Institute, Shenzhen, 518057, China

    Jintao Cui

  4. School of Mathematics and Information Sciences, Yantai University, Yantai, 264005, China

    Zhifeng Wang

Authors
  1. Wei Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jintao Cui
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhifeng Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jintao Cui.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The work of Wei Liu was supported by Shandong Provincial Natural Science Foundation No. ZR2019MA049 and in part by The Hong Kong Polytechnic University AMSS-PolyU Joint Research Institute (JRI) 1-ZVA8. Jintao Cui’s research is supported in part by the Hong Kong RGC, General Research Fund (GRF) Grant No. 15302518 and the National Natural Science Foundation of China (NSFC) Grant No. 11771367.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, W., Cui, J. & Wang, Z. A New Numerical Method for an Asymptotic Coupled Model of Fractured Media Aquifer System. J Sci Comput 82, 9 (2020). https://doi.org/10.1007/s10915-019-01112-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-019-01112-z

Keywords

Mathematics Subject Classification