Skip to main content
Springer Nature Link
Log in

Galerkin Boundary Element Methods for High-Frequency Multiple-Scattering Problems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

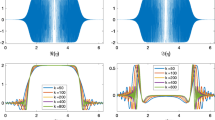
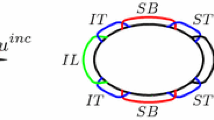
We consider high-frequency multiple-scattering problems in the exterior of two-dimensional smooth scatterers consisting of finitely many compact, disjoint, and strictly convex obstacles. To deal with this problem, we propose Galerkin boundary element methods, namely the frequency-adapted Galerkin boundary element methods and Galerkin boundary element methods generated using frequency-dependent changes of variables. For both of these new algorithms, in connection with each multiple-scattering iterate, we show that the number of degrees of freedom needs to increase as \(\mathcal {O}(k^{\epsilon })\) (for any \(\epsilon >0\)) with increasing wavenumber k to attain frequency-independent error tolerances. We support our theoretical developments by a variety of numerical implementations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Abboud, T., Nédélec, J.C., Zhou, B.: Méthode des équations intégrales pour les hautes fréquences. C. R. Acad. Sci. Paris Sér. I Math. 318(2), 165–170 (1994)

    MathSciNet  MATH  Google Scholar 

  2. Abboud, T., Nédélec, J.C., Zhou, B.: Improvements of the integral equation method for high frequency problems. In: Proceedings of 3rd International Conference on Mathematical Aspects of Wave Propagation Problems (1995)

  3. Amini, S., Profit, A.: Multi-level fast multipole solution of the scattering problem. Eng. Anal. Bound. Elem. 27(5), 547–564 (2003)

    MATH  Google Scholar 

  4. Anand, A., Boubendir, Y., Ecevit, F., Reitich, F.: Analysis of multiple scattering iterations for high-frequency scattering problems. II. The three-dimensional scalar case. Numer. Math. 114(3), 373–427 (2010)

    MathSciNet  MATH  Google Scholar 

  5. Antoine, X.: Advances in the on-surface radiation condition method: theory, numerics and applications. In: Magoulès, F. (ed.) Computational Methods for Acoustics Problems, pp. 169–194. Saxe-Coburg Publications, Stirlingshire (2008)

    Google Scholar 

  6. Banjai, L., Hackbusch, W.: Hierarchical matrix techniques for low- and high-frequency Helmholtz problems. IMA J. Numer. Anal. 28(1), 46–79 (2008)

    MathSciNet  MATH  Google Scholar 

  7. Boffi, D.: Finite element approximation of eigenvalue problems. Acta Numer. 19, 1–120 (2010)

    MathSciNet  MATH  Google Scholar 

  8. Boubendir, Y., Ecevit, F., Reitich, F.: Acceleration of an iterative method for the evaluation of high-frequency multiple scattering effects. SIAM J. Sci. Comput. 39(6), B1130–B1155 (2017)

    MathSciNet  MATH  Google Scholar 

  9. Bruno, O., Geuzaine, C., Reitich, F.: On the O(1) solution of multiple-scattering problems. IEEE Trans. Magn. 41(5), 1488–1491 (2005)

    Google Scholar 

  10. Bruno, O.P., Domínguez, V., Sayas, F.J.: Convergence analysis of a high-order Nyström integral-equation method for surface scattering problems. Numer. Math. 124(4), 603–645 (2013)

    MathSciNet  MATH  Google Scholar 

  11. Bruno, O.P., Geuzaine, C.A.: An O(1) integration scheme for three-dimensional surface scattering problems. J. Comput. Appl. Math. 204(2), 463–476 (2007)

    MathSciNet  MATH  Google Scholar 

  12. Bruno, O.P., Geuzaine, C.A., Monro Jr., J.A., Reitich, F.: Prescribed error tolerances within fixed computational times for scattering problems of arbitrarily high frequency: the convex case. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 362(1816), 629–645 (2004)

    MathSciNet  MATH  Google Scholar 

  13. Bruno, O.P., Kunyansky, L.A.: A fast, high-order algorithm for the solution of surface scattering problems: basic implementation, tests, and applications. J. Comput. Phys. 169(1), 80–110 (2001)

    MathSciNet  MATH  Google Scholar 

  14. Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Spence, E.A.: Numerical-asymptotic boundary integral methods in high-frequency acoustic scattering. Acta Numer. 21, 89–305 (2012)

    MathSciNet  MATH  Google Scholar 

  15. Chandler-Wilde, S.N., Hewett, D.P., Langdon, S., Twigger, A.: A high frequency boundary element method for scattering by a class of nonconvex obstacles. Numer. Math. 129(4), 647–689 (2015)

    MathSciNet  MATH  Google Scholar 

  16. Chandler-Wilde, S.N., Langdon, S.: A Galerkin boundary element method for high frequency scattering by convex polygons. SIAM J. Numer. Anal. 45(2), 610–640 (2007). (electronic)

    MathSciNet  MATH  Google Scholar 

  17. Chandler-Wilde, S.N., Langdon, S., Mokgolele, M.: A high frequency boundary element method for scattering by convex polygons with impedance boundary conditions. Commun. Comput. Phys. 11(2), 573–593 (2012)

    MathSciNet  MATH  Google Scholar 

  18. Colton, D., Kress, R.: Inverse Acoustic and Electromagnetic Scattering Theory, Applied Mathematical Sciences, vol. 93. Springer, Berlin (1992)

    MATH  Google Scholar 

  19. Davies, R.W., Morgan, K., Hassan, O.: A high order hybrid finite element method applied to the solution of electromagnetic wave scattering problems in the time domain. Comput. Mech. 44(3), 321–331 (2009)

    MathSciNet  MATH  Google Scholar 

  20. Domínguez, V.: Filon–Clenshaw–Curtis rules for a class of highly-oscillatory integrals with logarithmic singularities. J. Comput. Appl. Math. 261, 299–319 (2014)

    MathSciNet  MATH  Google Scholar 

  21. Domínguez, V., Graham, I.G., Smyshlyaev, V.P.: A hybrid numerical-asymptotic boundary integral method for high-frequency acoustic scattering. Numer. Math. 106(3), 471–510 (2007)

    MathSciNet  MATH  Google Scholar 

  22. Ecevit, F.: Frequency independent solvability of surface scattering problems. Turk. J. Math. 42(2), 407–422 (2018)

    MathSciNet  MATH  Google Scholar 

  23. Ecevit, F., Eruslu, H.H.: A Galerkin BEM for high-frequency scattering problems based on frequency-dependent changes of variables. IMA J. Numer. Anal. 39(2), 893–923 (2019)

    MathSciNet  Google Scholar 

  24. Ecevit, F., Özen, H.Ç.: Frequency-adapted galerkin boundary element methods for convex scattering problems. Numer. Math. 135(1), 27–71 (2017)

    MathSciNet  MATH  Google Scholar 

  25. Ecevit, F., Reitich, F.: Analysis of multiple scattering iterations for high-frequency scattering problems. I. The two-dimensional case. Numer. Math. 114(2), 271–354 (2009)

    MathSciNet  MATH  Google Scholar 

  26. Engquist, B., Majda, A.: Absorbing boundary conditions for the numerical simulation of waves. Math. Comput. 31(139), 629–651 (1977)

    MathSciNet  MATH  Google Scholar 

  27. Gibbs, A., Chandler-Wilde, S., Langdon, S., Moiola, A.: A high frequency boundary element method for scattering by a class of multiple obstacles (2019). arXiv:1903.04449

  28. Giladi, E.: Asymptotically derived boundary elements for the Helmholtz equation in high frequencies. J. Comput. Appl. Math. 198(1), 52–74 (2007)

    MathSciNet  MATH  Google Scholar 

  29. Givoli, D.: High-order local non-reflecting boundary conditions: a review. Wave Motion 39(4), 319–326 (2004). New computational methods for wave propagation

    MathSciNet  MATH  Google Scholar 

  30. Grote, M.J., Kirsch, C.: Nonreflecting boundary condition for time-dependent multiple scattering. J. Comput. Phys. 221(1), 41–62 (2007)

    MathSciNet  MATH  Google Scholar 

  31. Grote, M.J., Sim, I.: Local nonreflecting boundary condition for time-dependent multiple scattering. J. Comput. Phys. 230(8), 3135–3154 (2011)

    MathSciNet  MATH  Google Scholar 

  32. Groth, S., Hewett, D., Langdon, S.: A hybrid numerical-asymptotic boundary element method for high frequency scattering by penetrable convex polygons. Wave Motion 78, 32–53 (2018)

    MathSciNet  Google Scholar 

  33. Groth, S.P., Hewett, D.P., Langdon, S.: Hybrid numerical-asymptotic approximation for high-frequency scattering by penetrable convex polygons. IMA J. Appl. Math. 80(2), 324–353 (2013)

    MathSciNet  MATH  Google Scholar 

  34. Hesthaven, J., Warburton, T.: High-order accurate methods for time-domain electromagnetics. CMES Comput. Model. Eng. Sci. 5(5), 395–407 (2004)

    MATH  Google Scholar 

  35. Hewett, D.P.: Shadow boundary effects in hybrid numerical-asymptotic methods for high-frequency scattering. Eur. J. Appl. Math. 26(5), 773–793 (2015)

    MathSciNet  MATH  Google Scholar 

  36. Hewett, D.P., Langdon, S., Chandler-Wilde, S.N.: A frequency-independent boundary element method for scattering by two-dimensional screens and apertures. IMA J. Numer. Anal. 35(4), 1698–1728 (2014)

    MathSciNet  MATH  Google Scholar 

  37. Hewett, D.P., Langdon, S., Melenk, J.M.: A high frequency $hp$ boundary element method for scattering by convex polygons. SIAM J. Numer. Anal. 51(1), 629–653 (2013)

    MathSciNet  MATH  Google Scholar 

  38. Huybrechs, D., Vandewalle, S.: A sparse discretization for integral equation formulations of high frequency scattering problems. SIAM J. Sci. Comput. 29(6), 2305–2328 (2007)

    MathSciNet  MATH  Google Scholar 

  39. Langdon, S., Mokgolele, M., Chandler-Wilde, S.: High frequency scattering by convex curvilinear polygons. J. Comput. Appl. Math. 234(6), 2020–2026 (2010)

    MathSciNet  MATH  Google Scholar 

  40. Spence, E.A., Chandler-Wilde, S.N., Graham, I.G., Smyshlyaev, V.P.: A new frequency-uniform coercive boundary integral equation for acoustic scattering. Commun. Pure Appl. Math. 64(10), 1384–1415 (2011)

    MathSciNet  MATH  Google Scholar 

  41. Tong, M.S., Chew, W.C.: Multilevel fast multipole acceleration in the Nyström discretization of surface electromagnetic integral equations for composite objects. IEEE Trans. Antennas Propag. 58(10), 3411–3416 (2010)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Boğaziçi University, Bebek TR, 34342, Istanbul, Turkey

    Fatih Ecevit

  2. Department of Mathematics and Statistics, Indian Institute of Technology Kanpur, 327 Faculty Building, Kanpur, UP, 208016, India

    Akash Anand

  3. Department of Mathematical Sciences, New Jersey Institute of Technology, University Heights, Newark, NJ, 07102, USA

    Yassine Boubendir

Authors
  1. Fatih Ecevit
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Akash Anand
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yassine Boubendir
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Fatih Ecevit.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

F. Ecevit’s work was supported by The Scientific and Technological Research Council of Turkey through grant number TÜBİTAK-1001-117F056. A. Anand gratefully acknowledges support from IITK-ISRO Space Technology Cell through contract No. STC/MATH/2014100. Y. Boubendir’s work was supported by the NSF through Grant DMS-1720014.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ecevit, F., Anand, A. & Boubendir, Y. Galerkin Boundary Element Methods for High-Frequency Multiple-Scattering Problems. J Sci Comput 83, 1 (2020). https://doi.org/10.1007/s10915-020-01189-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01189-x

Keywords

Mathematics Subject Classification