Skip to main content
SpringerLink
Log in

Regularization Technique for an Inverse Space-Fractional Backward Heat Conduction Problem

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

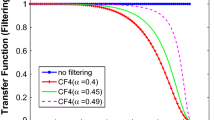
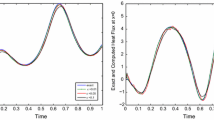
This manuscript deals with a regularization technique for a generalized space-fractional backward heat conduction problem (BHCP) which is well-known to be extremely ill-posed. The presented technique is developed based on the Meyer wavelets in retrieving the solution of the presented space-fractional BHCP. Some sharp optimal estimates of the Hölder-Logarithmic type are theoretically derived by imposing an a-priori bound assumption via the Sobolev scale. The existence, uniqueness and stability of the considered problem are rigorously investigated. The asymptotic error estimates for both linear and non-linear problems are all the same. Finally, the performance of the proposed technique is demonstrated through one- and two-dimensional prototype examples that validate our theoretical analysis. Furthermore, comparative results verify that the proposed method is more effective than the other existing methods in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Isakov, V.: Inverse Problems for Partial Differential Equation. Springer, New York (1998)

    MATH  Google Scholar 

  2. Carasso, A.S., Sanderson, J.G., Hyman, J.M.: Digital removal of random media image degradations by solving the diffusion equation backwards in time. SIAM J. Numer. Anal. 15(2), 344–367 (1978)

    MathSciNet  MATH  Google Scholar 

  3. Lee, L., Sheen, D.: A parallel method for backward parabolic problem based on the Laplace transformation. SIAM J. Numer. Anal. 44, 1466–1486 (2006)

    MathSciNet  MATH  Google Scholar 

  4. Li, M., Xiong, X.: On a fractional backward heat conduction problem: application to deblurring. Comput. Math. Appl. 64, 2594–2602 (2012)

    MathSciNet  MATH  Google Scholar 

  5. Nama, P.T., Trong, D.D., Tuan, N.H.: The truncation method for a two-dimensional nonhomogeneous backward heat problem. Appl. Math. Comput. 216, 3423–3432 (2010)

    MathSciNet  MATH  Google Scholar 

  6. Qiu, C., Feng, X.: A wavelet method for solving backward heat conduction problems. J. Differ. Equ. 219, 1–19 (2017)

    MATH  Google Scholar 

  7. Han, H., Ingham, D.B., Yuan, Y.: The boundary element method for the solution of the backward heat conduction equation. J. Comput. Phys. 116, 292–299 (1995)

    MATH  Google Scholar 

  8. Qian, Z., Fu, C.L., Shi, R.: A modified method for a backward heat conduction problem. Appl. Math. Comput. 185, 564–573 (2007)

    MathSciNet  MATH  Google Scholar 

  9. Karimi, M., Rezaee, A.R.: Regularization of the Cauchy problem for the Helmholtz equation by using Meyer wavelet. J. Comput. Appl. Math. 320, 79–95 (2017)

    MathSciNet  MATH  Google Scholar 

  10. Karimi, M., Moradlou, F., Hajipour, M.: On regularization and error estimates for the backward heat conduction problem with time-dependent thermal diffusivity factor. Commun. Nonlinear Sci. Numer. Simul 63, 21–37 (2018)

    MathSciNet  Google Scholar 

  11. Hatano, Y., Hatano, N.: Dispersive transport of ions in column experiments: an explanation of long-tailed profiles. Water Resour. 34, 1027–1033 (1998)

    Google Scholar 

  12. Ginoa, M., Cerbelli, S., Roman, H.E.: Fractional diffusion equation and relaxation in complex viscoelastic materials. Phys. A. 191, 449–453 (1992)

    Google Scholar 

  13. Metzler, R., Klafter, J.: Boundary value problems for fractional diffusion equations. Phys. A. 278, 107–125 (2000)

    MathSciNet  MATH  Google Scholar 

  14. Nigmatulin, R.: The realization of the generalized transfer equation in a medium with fractal geometry. Phys. Stat. Sol. B. 133, 425–430 (1986)

    Google Scholar 

  15. Gorenflo, R., Mainardi, F.: Fractional Calculus: Integral and Differential Equations of Fractional Order. Fractals and Fractional Calculus in Continuum Mechanics, pp. 223–276. Springer, New York (1997)

    Google Scholar 

  16. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  17. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  18. Chen, Z.Q., Meerschaert, M.M., Nane, E.: Space-time fractional diffusion on bounded domains. J. Math. Anal. Appl. 393, 479–488 (2012)

    MathSciNet  MATH  Google Scholar 

  19. Celik, C., Duman, M.: Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J. Comput. Phys. 231, 1743–1750 (2012)

    MathSciNet  MATH  Google Scholar 

  20. Ray, S.S.: A new approach for the application of Adomian decomposition method for the solution of fractional space diffusion equation with insulated ends. Appl. Math. Comput. 202, 544–549 (2008)

    MathSciNet  MATH  Google Scholar 

  21. Rahmana, M., Mahmooda, A., Younis, M.: Improved and more feasible numerical methods for Riesz space fractional partial differential equations. Appl. Math. Comput. 237, 264–273 (2014)

    MathSciNet  Google Scholar 

  22. Zheng, G.H., Wei, T.: Two regularization methods for solving a Riesz-Feller space-fractional backward diffusion problem. Inverse Prob. 26, 115017 (2010)

    MathSciNet  MATH  Google Scholar 

  23. Zheng, G.H., Zhang, Q.G.: Solving the backward problem for space-fractional diffusion equation by a fractional Tikhonov regularization method. Math. Comput. Simul. 148, 37–47 (2018)

    MathSciNet  Google Scholar 

  24. Zheng, G.H.: Solving the backward problem in Riesz-Feller fractional diffusion by a new nonlocal regularization method. Appl. Numer. Math. 135, 99–128 (2019)

    MathSciNet  MATH  Google Scholar 

  25. Jia, J., Peng, J., Gao, J., Li, Y.: Backward problem for a time-space fractional diffusion equation. Inverse. Probl. Imaging 12, 773–799 (2018)

    MathSciNet  MATH  Google Scholar 

  26. Kaltenbacher, B., Rundell, W.: Regularization of a backwards parabolic equation by fractional operators. Inverse. Probl. Imaging 13, 401–430 (2019)

    MathSciNet  MATH  Google Scholar 

  27. Khieu, T.T., Vo, H.H.: Recovering the historical distribution for nonlinear space-fractional diffusion equation with temporally dependent thermal conductivity in higher dimensional space. J. Comput. Math. Appl. 345, 114–126 (2019)

    MathSciNet  MATH  Google Scholar 

  28. Tuan, N.H., Hai, D.N.D., Long, L.D., Neuyen, V.T., Kirane, M.: On a Riesz-Feller space fractional backward diffusion problem with a nonlinear source. J. Comput. Appl. Math. 312, 103–126 (2017)

    MathSciNet  MATH  Google Scholar 

  29. Dou, F.F., Hon, Y.C.: Fundamental kernel-based method for backward space-time fractional diffusion problem. Comput. Math. Appl. 71, 356–367 (2016)

    MathSciNet  Google Scholar 

  30. Li, Y.S., Wei, T.: An inverse time-dependent source problem for a time-space fractional diffusion equation. Appl. Math. Comput. 336, 257–271 (2018)

    MathSciNet  MATH  Google Scholar 

  31. Meyer, M.: Wavelets and Operators. Cambridge University Press, Cambridge (1992)

    MATH  Google Scholar 

  32. Debnath, L.: Wavelet Transforms and Their Applications. Birkhäuser, Boston (2002)

    MATH  Google Scholar 

  33. Daubechies, I.: Ten Lectures on Wavelets. SIAM, Philadelphia, PA (1992)

    MATH  Google Scholar 

  34. Kolaczyk, E.D.: Wavelet methods for the inversion of certain homogeneous linear operators in the presence of noisy data. Ph.D. Thesis, Department of Statistics, Stanford University, Stanford, CA 94305-4065, (1994)

  35. Regińska, T.: Sideways heat equation and wavelets. J. Comput. Appl. Math 63, 209–214 (1995)

    MathSciNet  MATH  Google Scholar 

  36. Reginska, T., Eldén, L.: Solving the sideways heat equation by a wavelet-Galerkin method. Inverse Prob. 13, 1093–1106 (1997)

    MathSciNet  MATH  Google Scholar 

  37. Hao, D.N., Schneider, A., Reinhardt, H.J.: Regularization of a non-characteristic Cauchy problem for a parabolic equation. Inverse Prob. 11, 1247–1263 (1995)

    MathSciNet  MATH  Google Scholar 

  38. Wang, J.W.: Uniform convergence of wavelet solution to the sideways heat equation. Acta Math. Sin. (Engl. Ser.) 10(26), 1981–1992 (2010)

    MathSciNet  MATH  Google Scholar 

  39. Feng, X.L., Ning, W.T.: A wavelet regularization method for solving numerical analytic continuation. Int. J. Comput. Math. 92, 1025–1038 (2015)

    MathSciNet  MATH  Google Scholar 

  40. Qiu, C.Y., Fu, C.L.: Wavelets and regularization of the Cauchy problem for the Laplace equation. J. Math. Anal. Appl. 338(2), 1440–1447 (2008)

    MathSciNet  MATH  Google Scholar 

  41. Vani, C., Avudainayagam, A.: Regularized solution of the Cauchy problem for the Laplace equation using Meyer Wavelets. Math. Comput. Model. 36, 1151–1159 (2002)

    MathSciNet  MATH  Google Scholar 

  42. Regińska, T., Eldén, T.: Stability and convergence of a wavelet-Galerkin method for the sideways heat equation. J. Inverse Ill-Posed Probl. 8, 31–49 (2000)

    MathSciNet  MATH  Google Scholar 

  43. Eldén, L., Berntsson, F., Regińska, T.: Wavelet and Fourier methods for solving the sideways heat equation. SIAM J. Sci. Comput. 21, 2178–2205 (2000)

    MathSciNet  MATH  Google Scholar 

  44. Nezza, L.D., Palatucci, G., Valdinoci, E.: Hitchhiker’s guide to the fractional Sobolev spaces. Bulletin des Sciences Mathématiques 136, 521–573 (2012)

    MathSciNet  MATH  Google Scholar 

  45. Shang, X., Zhang, J.: Ground states for fractional Schrödinger equations with critical growth. Nonlinearity 27, 187 (2014)

    MathSciNet  MATH  Google Scholar 

  46. Tautenhahen, U.: Optimality for ill-posed problems under general source conditions. Zeitschrift für Analysis und ihre Anwendungen. 19, 377–398 (1998)

    MathSciNet  Google Scholar 

  47. Hào, D.N., Reinhardt, H.J., Schneider, A.: Stable approximation of fractional derivatives of rough functions. BIT. 35, 488 (1995)

    MathSciNet  MATH  Google Scholar 

  48. Tautenhahen, U., Schröter, T.: On optimal regularization methods for the backward heat equation. Numer. Funct. Anal. Optim. 15, 475–493 (1996)

    MathSciNet  MATH  Google Scholar 

  49. Tautenhahen, U.: Optimal stable approximations for the sideways heat equation. J. Inverse Ill-Posed Probl. 5, 287–307 (1997)

    MathSciNet  Google Scholar 

  50. Zhang, H., Liu, F., Anh, V.: Numerical approximation of Ĺevy-Feller diffusion equation and its probability interpretation. J. Comput. Appl. Math. 206(2), 1098–1115 (2007)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Sahand University of Technology, P.O. Box: 51335-1996, Tabriz, Iran

    Milad Karimi, Fridoun Moradlou & Mojtaba Hajipour

Authors
  1. Milad Karimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fridoun Moradlou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mojtaba Hajipour
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fridoun Moradlou.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Karimi, M., Moradlou, F. & Hajipour, M. Regularization Technique for an Inverse Space-Fractional Backward Heat Conduction Problem. J Sci Comput 83, 37 (2020). https://doi.org/10.1007/s10915-020-01211-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01211-2

Keywords

Search

Navigation