Skip to main content
Springer Nature Link
Log in

Penalty-Free Any-Order Weak Galerkin FEMs for Elliptic Problems on Quadrilateral Meshes

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

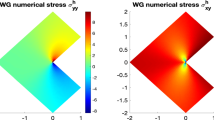
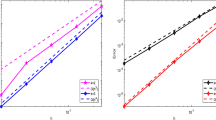
Abstract

This paper presents a family of weak Galerkin finite element methods for elliptic boundary value problems on convex quadrilateral meshes. These new methods use degree \(k \ge 0\) polynomials separately in element interiors and on edges for approximating the primal variable. The discrete weak gradients of these shape functions are established in the local Arbogast–Correa \(AC_k \) spaces. These discrete weak gradients are then used to approximate the classical gradient in the variational formulation. These new methods do not use any nonphysical penalty factor but produce optimal-order approximation to the primal variable, flux, normal flux, and divergence of flux. Moreover, these new solvers are locally conservative and offer continuous normal fluxes. Numerical experiments are presented to demonstrate the accuracy of this family of new methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Arbogast, T., Correa, M.: Two families of H(div) mixed finite elements on quadrilaterals of minimal dimension. SIAM J. Numer. Anal. 54, 3332–3356 (2016)

    Article  MathSciNet  Google Scholar 

  2. Arbogast, T., Tao, Z.: Construction of H(div)-conforming mixed finite elements on cuboidal hexahedra. Numer. Math. 142, 1–32 (2019)

    Article  MathSciNet  Google Scholar 

  3. Arbogast, T., Wheeler, M.F., Yotov, I.: Mixed finite elements for elliptic problems with tensor coefficients as cell-centered finite differences. SIAM J. Numer. Anal. 34, 828–852 (1997)

    Article  MathSciNet  Google Scholar 

  4. Arnold, D., Boffi, D., Falk, R.: Approximation by quadrilateral finite elements. Math. Comput. 71, 909–922 (2002)

    Article  MathSciNet  Google Scholar 

  5. Arnold, D., Boffi, D., Falk, R.: Quadrilateral H(div) finite elements. SIAM J. Numer. Anal. 42, 2429–2451 (2005)

    Article  MathSciNet  Google Scholar 

  6. Arnold, D.N., Brezzi, F.: Mixed and nonconforming finite element methods: implementation, postprocessing and error estimates. Math. Model. Numer. Anal. 19, 7–32 (1985)

    Article  MathSciNet  Google Scholar 

  7. Brezzi, F., Fortin, M.: Mixed and hybrid finite element methods. Springer, Berlin (1991)

    Book  Google Scholar 

  8. Bush, L., Ginting, V.: On the application of the continuous Galerkin finite element method for conservation problems. SIAM J. Sci. Comput. 35, A2953–A2975 (2013)

    Article  MathSciNet  Google Scholar 

  9. Chen, W., Wang, F., Wang, Y.: Weak Galerkin method for the coupled Darcy–Stokes flow. IMA J. Numer. Anal. 36, 897–921 (2016)

    Article  MathSciNet  Google Scholar 

  10. Cockburn, B.: Static condensation, hybridization, and the devising of the HDG methods. In: Barrenechea, G.R., Brezzi, F. (eds.) Building Bridges: Connection and Challenges in Modern Approaches to Numerical Partial Differential Equations, pp. 129–177. Springer, Berlin (2016)

    Chapter  Google Scholar 

  11. Cockburn, B., Fu, G., Sayas, F.-J.: Superconvergence by M-decompositions. Part I: general theory for HDG methods for diffusion. Math. Comput. 86, 1609–1641 (2017)

    Article  MathSciNet  Google Scholar 

  12. Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47, 1319–1365 (2009)

    Article  MathSciNet  Google Scholar 

  13. Cockburn, B., Qiu, W., Shi, K.: Superconvergent HDG methods on isoparametric elements for second-order elliptic problems. SIAM J. Numer. Anal. 50, 1417–1432 (2012)

    Article  MathSciNet  Google Scholar 

  14. Ginting, V., Lin, G., Liu, J.: On application of the weak Galerkin finite element method to a two-phase model for subsurface flow. J. Sci. Comput. 66, 225–239 (2016)

    Article  MathSciNet  Google Scholar 

  15. Harper, G., Liu, J., Tavener, S., Zheng, B.: Lowest-order weak Galerkin finite element methods for linear elasticity on rectangular and brick meshes. J. Sci. Comput. 78(3), 1917–1941 (2019)

    Article  MathSciNet  Google Scholar 

  16. Ingram, R., Wheeler, M.F., Yotov, I.: A multipoint flux mixed finite element method on hexahedra. SIAM J. Numer. Anal. 48, 1281–1312 (2010)

    Article  MathSciNet  Google Scholar 

  17. Lin, G., Liu, J., Mu, L., Ye, X.: Weak Galerkin finite element methods for Darcy flow: anistropy and heterogeneity. J. Comput. Phys. 276, 422–437 (2014)

    Article  MathSciNet  Google Scholar 

  18. Liu, J., Cali, R.: A note on the approximation properties of the locally divergence-free finite elements. Int. J. Numer. Anal. Model. 5, 693–703 (2008)

    MathSciNet  MATH  Google Scholar 

  19. Liu, J., Tavener, S., Wang, Z.: The lowest-order weak Galerkin finite element methods for the Darcy equation on quadrilateral and hybrid meshes. J. Comput. Phys. 359, 312–330 (2018)

    Article  MathSciNet  Google Scholar 

  20. Mu, L., Wang, J., Ye, X.: Weak Galerkin finite element methdos on polytopal meshes. Int. J. Numer. Anal. Model. 12, 31–53 (2015)

    MathSciNet  MATH  Google Scholar 

  21. Mu, L., Wang, J., Ye, X.: A weak Galerkin finite element method with polynomial reduction. J. Comput. Appl. Math. 285, 45–58 (2015)

    Article  MathSciNet  Google Scholar 

  22. Mu, L., Wang, J., Ye, X., Zhang, S.: A discrete divergence free weak Galerkin finite element method for the Stokes equations. Appl. Numer. Math. 125, 172–182 (2018)

    Article  MathSciNet  Google Scholar 

  23. Sun, S., Liu, J.: A locally conservative finite element method based on piecewise constant enrichment of the continuous Galerkin method. SIAM J. Sci. Comput. 31, 2528–2548 (2009)

    Article  MathSciNet  Google Scholar 

  24. Wang, C., Wang, J., Wang, R., Zhang, R.: A locking-free weak Galerkin finite element method for elasticity problems in the primal formulation. J. Comput. Appl. Math. 307, 346–366 (2016)

    Article  MathSciNet  Google Scholar 

  25. Wang, J., Ye, X.: A weak Galerkin finite element method for second order elliptic problems. J. Comput. Appl. Math. 241, 103–115 (2013)

    Article  MathSciNet  Google Scholar 

  26. Wang, J., Ye, X.: A weak Galerkin mixed finite element method for second order elliptic problems. Math. Comput. 83, 2101–2126 (2014)

    Article  MathSciNet  Google Scholar 

  27. Wheeler, M., Xue, G., Yotov, I.: A multipoint flux mixed finite element method on distorted quadrilaterals and hexahedra. Numer. Math. 121, 165–204 (2012)

    Article  MathSciNet  Google Scholar 

  28. Wihler, T., Riviére, B.: Discontinuous Galerkin methods for second-order elliptic PDE with low-regularity solutions. J. Sci. Comput. 46, 151–165 (2011)

    Article  MathSciNet  Google Scholar 

  29. Yi, S.-Y.: A lowest-order weak Galerkin method for linear elasticity. J. Comput. Appl. Math. 350, 286–298 (2019)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

J. Liu and Z. Wang were supported in part by US National Science Foundation under Grant DMS-1819252. S. Tavener was supported in part by US National Science Foundation under Grant DMS-1720473. We sincerely thank the anonymous reviewers for their constructive comments, which have helped improve the quality of this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Colorado State University, Fort Collins, CO, 80523-1874, USA

    Jiangguo Liu, Simon Tavener & Zhuoran Wang

Authors
  1. Jiangguo Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Simon Tavener
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhuoran Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jiangguo Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

J. Liu and Z. Wang were partially supported by US NSF under Grant DMS-1819252. S. Tavener was partially supported by US NSF under Grant DMS-1720473.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, J., Tavener, S. & Wang, Z. Penalty-Free Any-Order Weak Galerkin FEMs for Elliptic Problems on Quadrilateral Meshes. J Sci Comput 83, 47 (2020). https://doi.org/10.1007/s10915-020-01239-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01239-4

Keywords

Mathematics Subject Classification