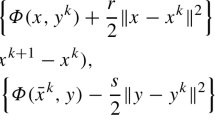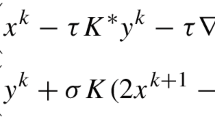Skip to main content
Springer Nature Link
Log in

A Double Extrapolation Primal-Dual Algorithm for Saddle Point Problems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

The first-order primal-dual algorithms have received much considerable attention in the literature due to their quite promising performance in solving large-scale image processing models. In this paper, we consider a general saddle point problem and propose a double extrapolation primal-dual algorithm, which employs the efficient extrapolation strategy for both primal and dual variables. It is remarkable that the proposed algorithm enjoys a unified framework including several existing efficient solvers as special cases. Another exciting property is that, under quite flexible requirements on the involved extrapolation parameters, our algorithm is globally convergent to a saddle point of the problem under consideration. Moreover, the worst case \({{\mathcal {O}}}(1/t)\) convergence rate in both ergodic and nonergodic senses, and the linear convergence rate can be established for more general cases, where t counts the iteration. Some computational results on solving image deblurring, image inpainting and the nearest correlation matrix problems further show that the proposed algorithm is efficient, and performs better than some existing first-order solvers in terms of taking less iterations and computing time in some cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3, 1–122 (2010)

    Article  Google Scholar 

  2. Cai, X., Han, D., Xu, L.: An improved first-order primal-dual algorithm with a new correction step. J. Global Optim. 57, 1419–1428 (2013)

    Article  MathSciNet  Google Scholar 

  3. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40, 120–145 (2011)

    Article  MathSciNet  Google Scholar 

  4. Chambolle, A., Pock, T.: On the ergodic convergence rates of a first order primal dual algorithm. Math. Program. Ser. A 159, 253–287 (2016)

    Article  MathSciNet  Google Scholar 

  5. Chen, C., Chan, R., Ma, S., Yang, J.: Intertial prxoimal ADMM for linearly constrained separable convex optimization. SIAM J. Imaging Sci. 8(4), 2239–2267 (2015)

    Article  MathSciNet  Google Scholar 

  6. Chen, Y., Lan, G., Ouyang, Y.: Optimal primal dual methods for a class of saddle point problems. SIAM J. Optim. 24, 1779–1814 (2014)

    Article  MathSciNet  Google Scholar 

  7. Deng, W., Yin, W.: On the global and linear convergence of the generalized alternating direction method of multipliers. J. Sci. Comput. 66(3), 889–916 (2016)

    Article  MathSciNet  Google Scholar 

  8. Du, S., Hu, W.: Linear convergence of the primal-dual gradient method for convex-concave saddle point problems without strong convexity. In: Proceedings of the 22nd International Conference on Atificial Intelligence and Statistics, pp. 196–205 (2019)

  9. Esser, E., Zhang, X., Chan, T.: A general framework for a class of first-order primal-dual algorithms for convex optimization in imaging sciences. SIAM J. Imaging Sci. 3, 1015–1046 (2010)

    Article  MathSciNet  Google Scholar 

  10. Facchinei, F., Pang, J.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, New York (2003)

    MATH  Google Scholar 

  11. Gao, Y., Sun, D.: Calibrating least squares semidefinite programming with equality and inequality constraints. SIAM J. Matrix Anal. Appl. 31(2), 1432–1457 (2009)

    MathSciNet  MATH  Google Scholar 

  12. Glowinski, R., Marrocco, A.: Approximation par éléments finis d’ordre un et résolution par pénalisation-dualité d’une classe de problèmes non linéaires. R.A.I.R.O. R2, 41–76 (1975)

  13. Gu, G., He, B., Yuan, X.: Customized proximal point algorithms for linearly constrained convex minimization and saddle-point problems: A uniform approach. Comput. Optim. Appl. 59, 135–161 (2014)

    Article  MathSciNet  Google Scholar 

  14. Han, D., Sun, D., Zhang, L.: Linear rate convergence of the alternating direction method of multipliers for convex composite programming. Math. Oper. Res. 43(2), 622–637 (2018)

    Article  MathSciNet  Google Scholar 

  15. Han, D., Xu, W., Yang, H.: An operator splitting method for variational inequalities with partially unknown mappings. Numer. Math. 111, 207–237 (2008)

    Article  MathSciNet  Google Scholar 

  16. He, B., Ma, F., Yuan, X.: An algorithmic framework of generalized primal-dual hybrid gradient methods for saddle point problems. J Math. Imaging Vis. 58(2), 279–293 (2017)

    Article  MathSciNet  Google Scholar 

  17. He, B., Xu, M., Yuan, X.: Solving large-scale least squares covariance matrix problems by alternating direction methods. SIAM J. Matrix Anal. Appl. 32, 136–152 (2011)

    Article  MathSciNet  Google Scholar 

  18. He, B., You, Y., Yuan, X.: On the convergence of primal dual hybrid gradient algorithm. SIAM J. Imaging Sci. 7, 2526–2537 (2015)

    Article  MathSciNet  Google Scholar 

  19. He, B., Yuan, X.: Convergence analysis of primal-dual algorithms for a saddle-point problem: From contraction perspective. SIAM J. Imaging Sci. 5, 119–149 (2012)

    Article  MathSciNet  Google Scholar 

  20. He, H., Desai, J., Wang, K.: A primal-dual prediction-correction algorithm for saddle point optimization. J. Global Optim. 66(3), 573–583 (2016)

    Article  MathSciNet  Google Scholar 

  21. Hong, M., Luo, Z.: On the linear convergence of alternating direction method of multipliers. Math. Program. Ser. A 162(1–2), 165–199 (2017)

    Article  MathSciNet  Google Scholar 

  22. Lin, T., Ma, S., Zhang, S.: An extragradient-based alternating direction method for convex minimization. Found. Comput. Math. 17, 35–59 (2017)

    Article  MathSciNet  Google Scholar 

  23. Lu, Z., Zhou, Z., Sun, Z.: Enhanced proximal DC algorithms with extrapolation for a class of structured nonsmooth DC minimization. Math. Program. Ser. B 176, 369–401 (2019)

    Article  MathSciNet  Google Scholar 

  24. Malitsky, Y., Pock, T.: A first-order primal-dual algorithm with linesearch. SIAM J. Optim. 28(1), 411–432 (2018)

    Article  MathSciNet  Google Scholar 

  25. Nemirovski, A.: Prox-method with rate of convergence \({O}(1/t)\) for variational inequalities with Lipschitz continuous monotone operator and smooth convex-concave saddle point problems. SIAM J. Optim. 15, 229–251 (2004)

    Article  MathSciNet  Google Scholar 

  26. Nesterov, Y.: Introductory Lectures on Convex Optimization: Basic Course. Kluwer, Boston (2003)

    MATH  Google Scholar 

  27. Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 4(5), 1–17 (1964)

    Article  Google Scholar 

  28. Rockafellar, R.: Convex Analysis. Princeton University Press, Princeton, NJ (1970)

    Book  Google Scholar 

  29. Sidi, A.: Practical Extrapolation Methods: Theory and Applications. Cambridge University Press, Cambridge (2003)

    Book  Google Scholar 

  30. Tian, W., Yuan, X.: Linearized primal-dual methods for linear inverse problems with total variation regularization and finite element discretization. Inverse Problems 32, 115011(32pp) (2016)

    Article  MathSciNet  Google Scholar 

  31. Wen, B., Chen, X., Pong, T.: Linear convergence of proximal gradient algorithm with extrapolation for a class of nonconvex nonsmooth minimization problems. SIAM J. Optim. 27(1), 124–145 (2017)

    Article  MathSciNet  Google Scholar 

  32. Yang, W., Han, D.: Linear convergence of the alternating direction method of multipliers for a class of convex optimization problems. SIAM J. Numer. Anal. 54(2), 625–640 (2016)

    Article  MathSciNet  Google Scholar 

  33. Zhang, X., Zhang, X.: A new proximal iterative hard thresholding method with extrapolation for \(\ell _0\) minimization. J. Sci. Comput. 79, 809–826 (2019)

    Article  MathSciNet  Google Scholar 

  34. Zheng, X., Ng, K.: Metric subregularity of piecewise linear multifunctions and applications to piecewise linear multiobjective optimization. SIAM J. Optim. 24(1), 154–174 (2014)

    Article  MathSciNet  Google Scholar 

  35. Zhu, M., Chan, T.: An efficient primal-dual hybrid gradient algorithm for total variation image restoration. CAM Reports 08-34, UCLA (2008)

Download references

Acknowledgements

The authors are grateful to the editor and two anonymous referees for their valuable comments which led to great improvements of the paper. K. Wang was supported by National Natural Science Foundation of China (NSFC) at Grant No. 11901294 and Natural Science Foundation of Jiangsu Province at Grant No. BK20190429. H. He was supported in part by NSFC (No. 11771113) and Natural Science Foundation of Zhejiang Province at Grant No. LY20A010018.

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Science, Nanjing University of Science and Technology, Xiaolingwei 200, Nanjing, 210094, China

    Kai Wang

  2. Department of Mathematics, School of Science, Hangzhou Dianzi University, Hangzhou, 310018, China

    Hongjin He

Authors
  1. Kai Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hongjin He
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hongjin He.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, K., He, H. A Double Extrapolation Primal-Dual Algorithm for Saddle Point Problems. J Sci Comput 85, 30 (2020). https://doi.org/10.1007/s10915-020-01330-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01330-w

Keywords

Mathematics Subject Classification