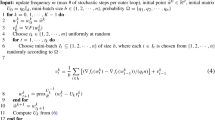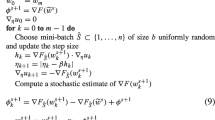Skip to main content
Springer Nature Link
Log in

Stochastic Variance Reduced Gradient Methods Using a Trust-Region-Like Scheme

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

Stochastic variance reduced gradient (SVRG) methods are important approaches to minimize the average of a large number of cost functions frequently arising in machine learning and many other applications. In this paper, based on SVRG, we propose a SVRG-TR method which employs a trust-region-like scheme for selecting stepsizes. It is proved that the SVRG-TR method is linearly convergent in expectation for smooth strongly convex functions and enjoys a faster convergence rate than SVRG methods. In order to overcome the difficulty of tuning stepsizes by hand, we propose to combine the Barzilai–Borwein (BB) method to automatically compute stepsizes for the SVRG-TR method, named as the SVRG-TR-BB method. By incorporating mini-batching scheme with SVRG-TR and SVRG-TR-BB, respectively, we further propose two extended methods mSVRG-TR and mSVRG-TR-BB. Linear convergence and complexity of mSVRG-TR are given. Numerical experiments on some standard datasets show that SVRG-TR and SVRG-TR-BB are generally better than or comparable to SVRG with best-tuned stepsizes and some modern stochastic gradient methods, while mSVRG-TR and mSVRG-TR-BB are very competitive with mini-batch variants of recent successful stochastic gradient methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. www.csie.ntu.edu.tw/~cjlin/libsvmtools/.

References

  1. Allen-Zhu, Z.: Katyusha: The first direct acceleration of stochastic gradient methods. In: Proc. 49th Annu. SIGACT STOC, pp. 1200–1205 (2017)

  2. Allen-Zhu, Z., Hazan, E.: Optimal black-box reductions between optimization objectives. In: Proc. 29th Int. Conf. Adv. Neural Inf. Process. Syst., pp. 1614–1622 (2016)

  3. Allen-Zhu, Z., Yuan, Y.: Improved SVRG for non-strongly-convex or sum-of-non-convex objectives. In: Int. Conf. Mach. Learn., pp. 1080–1089 (2016)

  4. Barzilai, J., Borwein, J.M.: Two-point step size gradient methods. IMA J. Numer. Anal. 8(1), 141–148 (1988)

    Article  MathSciNet  Google Scholar 

  5. Bonnabel, S.: Stochastic gradient descent on Riemannian manifolds. IEEE Trans. Autom. Control 58(9), 2217–2229 (2013)

    Article  MathSciNet  Google Scholar 

  6. Bottou, L.: Large-scale machine learning with stochastic gradient descent. In: Proc. COMPSTAT’2010, pp. 177–186. Springer (2010)

  7. Bottou, L., Curtis, F.E., Nocedal, J.: Optimization methods for large-scale machine learning. SIAM Rev. 60(2), 223–311 (2018)

    Article  MathSciNet  Google Scholar 

  8. Cardoso, J.F., Laheld, B.H.: Equivariant adaptive source separation. IEEE Trans. Signal Process. 44(12), 3017–3030 (1996)

    Article  Google Scholar 

  9. Chang, D., Lin, M., Zhang, C.: On the generalization ability of online gradient descent algorithm under the quadratic growth condition. IEEE Trans. Neural Netw. Learn. Syst. (2018)

  10. Chen, Z., Xu, Y., Chen, E., Yang, T.: Sadagrad: strongly adaptive stochastic gradient methods. In: Int. Conf. Mach. Learn., pp. 912–920 (2018)

  11. Cohen, K., Nedić, A., Srikant, R.: On projected stochastic gradient descent algorithm with weighted averaging for least squares regression. IEEE Trans. Autom. Control 62(11), 5974–5981 (2017)

    Article  MathSciNet  Google Scholar 

  12. Curtis, F.E., Scheinberg, K., Shi, R.: A stochastic trust region algorithm. arXiv preprint arXiv:1712.10277 (2017)

  13. Dai, Y.H., Al-Baali, M., Yang, X.: A positive Barzilai–Borwein-like stepsize and an extension for symmetric linear systems. In: Numer. Funct. Anal. Optim., pp. 59–75. Springer (2015)

  14. Dai, Y.H., Fletcher, R.: Projected Barzilai–Borwein methods for large-scale box-constrained quadratic programming. Numer. Math. 100(1), 21–47 (2005)

    Article  MathSciNet  Google Scholar 

  15. Defazio, A., Bach, F., Lacoste-Julien, S.: Saga: a fast incremental gradient method with support for non-strongly convex composite objectives. In: Proc. 27th Int. Conf. Adv. Neural Inf. Process. Syst., pp. 1646–1654 (2014)

  16. Frostig, R., Ge, R., Kakade, S., Sidford, A.: Un-regularizing: approximate proximal point and faster stochastic algorithms for empirical risk minimization. In: Int. Conf. Mach. Learn., pp. 2540–2548 (2015)

  17. Godard, D.: Self-recovering equalization and carrier tracking in two-dimensional data communication systems. IEEE Trans. Commun. 28(11), 1867–1875 (1980)

    Article  Google Scholar 

  18. Harikandeh, R., Ahmed, M.O., Virani, A., Schmidt, M., Konečnỳ, J., Sallinen, S.: Stopwasting my gradients: practical SVRG. In: Proc. 28th Int. Conf. Adv. Neural Inf. Process. Syst., pp. 2251–2259 (2015)

  19. Huang, Y., Liu, H.: Smoothing projected Barzilai–Borwein method for constrained non-Lipschitz optimization. Comput. Optim. Appl. 65(3), 671–698 (2016)

    Article  MathSciNet  Google Scholar 

  20. Huang, Y., Liu, H., Zhou, S.: A Barzilai–Borwein type method for stochastic linear complementarity problems. Numer. Algorithm 67(3), 477–489 (2014)

    Article  MathSciNet  Google Scholar 

  21. Huang, Y., Liu, H., Zhou, S.: Quadratic regularization projected Barzilai–Borwein method for nonnegative matrix factorization. Data Min. Knowl. Disc. 29(6), 1665–1684 (2015)

    Article  MathSciNet  Google Scholar 

  22. Jiang, B., Ma, S., So, A.M.C., Zhang, S.: Vector transport-free SVRG with general retraction for riemannian optimization: complexity analysis and practical implementation. arXiv preprint arXiv:1705.09059 (2017)

  23. Johnson, R., Zhang, T.: Accelerating stochastic gradient descent using predictive variance reduction. In: Proc. 26th Int. Conf. Adv. Neural Inf. Process. Syst., pp. 315–323 (2013)

  24. Konečnỳ, J., Liu, J., Richtárik, P., Takáč, M.: Mini-batch semi-stochastic gradient descent in the proximal setting. IEEE J. Sel. Top. Signal Process. 10(2), 242–255 (2016)

    Article  Google Scholar 

  25. Konečnỳ, J., Richtárik, P.: Semi-stochastic gradient descent methods. Front. Appl. Math. Stat. 3, 9 (2017)

    Article  Google Scholar 

  26. Kronvall, T., Adalbjörnsson, S.I., Nadig, S., Jakobsson, A.: Group-sparse regression using the covariance fitting criterion. Signal Process. 139, 116–130 (2017)

    Article  Google Scholar 

  27. Li, X.L.: Preconditioned stochastic gradient descent. IEEE Trans. Neural Netw. Learn. Syst. 29(5), 1454–1466 (2018)

    Article  MathSciNet  Google Scholar 

  28. Mairal, J.: Incremental majorization-minimization optimization with application to large-scale machine learning. SIAM J. Optim. 25(2), 829–855 (2015)

    Article  MathSciNet  Google Scholar 

  29. Mairal, J., Bach, F., Ponce, J., Sapiro, G.: Online dictionary learning for sparse coding. In: Proc. 26th Int. Conf. Mach. Learn., pp. 689–696 (2009)

  30. Mu, Y., Liu, W., Liu, X., Fan, W.: Stochastic gradient made stable: a manifold propagation approach for large-scale optimization. IEEE Trans. Knowl. Data Eng. 29(2), 458–471 (2017)

    Article  Google Scholar 

  31. Nesterov, Y.: Introductory Lectures on Convex Programming, vol. 1. Springer Science, New York (2004)

    Book  Google Scholar 

  32. Nguyen, L.M., Liu, J., Scheinberg, K., Takáč, M.: Sarah: a novel method for machine learning problems using stochastic recursive gradient. In: Int. Conf. Mach. Learn., pp. 2613–2621 (2017)

  33. Rakhlin, A., Shamir, O., Sridharan, K., et al.: Making gradient descent optimal for strongly convex stochastic optimization. In: Int. Conf. Mach. Learn., pp. 1571–1578 (2012)

  34. Robbins, H., Monro, S.: A stochastic approximation method. Ann. Math. Stat. pp. 400–407 (1951)

  35. Roux, N.L., Schmidt, M., Bach, F.R.: A stochastic gradient method with an exponential convergence rate for finite training sets. In: Proc. 25th Int. Conf. Adv. Neural Inf. Process. Syst., pp. 2663–2671 (2012)

  36. Shalev-Shwartz, S., Ben-David, S.: Understanding Machine Learning: From Theory to Algorithms. Cambridge University Press, Cambridge (2014)

    Book  Google Scholar 

  37. Sutskever, I., Martens, J., Dahl, G., Hinton, G.: On the importance of initialization and momentum in deep learning. In: Int. Conf. Mach. Learn., pp. 1139–1147 (2013)

  38. Tan, C., Ma, S., Dai, Y.H., Qian, Y.: Barzilai–Borwein step size for stochastic gradient descent. In: Proc. 29th Int. Conf. Adv. Neural Inf. Process. Syst., pp. 685–693 (2016)

  39. Wang, X., Ma, S., Goldfarb, D., Liu, W.: Stochastic quasi-Newton methods for nonconvex stochastic optimization. SIAM J. Optim. 27(2), 927–956 (2017)

    Article  MathSciNet  Google Scholar 

  40. Wen, Z., Yin, W., Goldfarb, D., Zhang, Y.: A fast algorithm for sparse reconstruction based on shrinkage, subspace optimization, and continuation. SIAM J. Sci. Comput. 32(4), 1832–1857 (2010)

    Article  MathSciNet  Google Scholar 

  41. Xiao, L., Zhang, T.: A proximal stochastic gradient method with progressive variance reduction. SIAM J. Optim. 24(4), 2057–2075 (2014)

    Article  MathSciNet  Google Scholar 

  42. Yang, Z., Wang, C., Zang, Y., Li, J.: Mini-batch algorithms with Barzilai–Borwein update step. Neurocomputing 314, 177–185 (2018)

    Article  Google Scholar 

  43. Yang, Z., Wang, C., Zhang, Z., Li, J.: Accelerated stochastic gradient descent with step size selection rules. Signal Process. 159, 171–186 (2019)

    Article  Google Scholar 

  44. Yuan, Y.-X.: Recent advances in trust region algorithms. Math. Program. 151(1), 249–281 (2015)

    Article  MathSciNet  Google Scholar 

  45. Zhang, L., Mahdavi, M., Jin, R.: Linear convergence with condition number independent access of full gradients. In: Proc. 26th Int. Conf. Adv. Neural Inf. Process. Syst., pp. 980–988 (2013)

  46. Zhang, T.: Solving large scale linear prediction problems using stochastic gradient descent algorithms. In: Int. Conf. Mach. Learn. (2004)

  47. Zhao, P., Zhang, T.: Stochastic optimization with importance sampling for regularized loss minimization. In: Int. Conf. Mach. Learn., pp. 1–9 (2015)

Download references

Author information

Authors and Affiliations

  1. School of Artificial Intelligence, Hebei University of Technology, Tianjin, 300401, China

    Tengteng Yu

  2. Institute of Mathematics, Hebei University of Technology, Tianjin, 300401, China

    Xin-Wei Liu & Jie Sun

  3. State Key Laboratory of Scientific and Engineering Computing, Institute of Computational Mathematics and Scientific/Engineering Computing, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    Yu-Hong Dai

  4. School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing, 100049, China

    Yu-Hong Dai

  5. School of Business, National University of Singapore, Singapore, 119245, Singapore

    Jie Sun

Authors
  1. Tengteng Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xin-Wei Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yu-Hong Dai
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jie Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xin-Wei Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The research is in part by the Chinese NSF under Grants 11671116, 11701137, 12071108, 11631013, 11991020, and 12021001; in part by the Major Research Plan of the NSFC under Grants 91630202, and in part by the Beijing Academy of Artificial Intelligence (BAAI).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, T., Liu, XW., Dai, YH. et al. Stochastic Variance Reduced Gradient Methods Using a Trust-Region-Like Scheme. J Sci Comput 87, 5 (2021). https://doi.org/10.1007/s10915-020-01402-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01402-x

Keywords

Mathematics Subject Classification