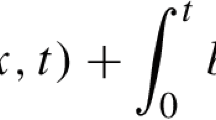Abstract
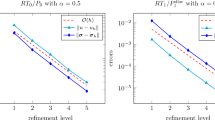
We study the space-time finite element discretizations for time fractional parabolic integro-differential equations in a bounded convex polygonal domain in \({\mathbb {R}}^d (d=1,2,3)\). Both spatially semidiscrete and fully discrete finite element approximations are considered and analyzed. We use piecewise linear and continuous finite elements to approximate the space variable whereas the time discretization uses two fully discrete schemes based on the convolution quadrature, namely the backward Euler and the second-order backward difference. For the spatially discrete scheme, optimal order a priori error estimates are derived for smooth initial data, i.e., when \(u_0\in H_0^1(\varOmega )\cap H^2(\varOmega )\). Moreover, for the homogeneous problem, almost optimal error estimates for positive time are established for nonsmooth initial data, i.e., when the initial function \(u_0\) is only in \( L^2(\varOmega )\). The error estimates for the fully discrete methods are shown to be optimal in time for both smooth and nonsmooth initial data under the specific choice of the kernel operator in the integral. Finally, we provide some numerical illustrations to verify our theoretical analysis.

Similar content being viewed by others
References
Amer, Y.A., Mahdy, A.M.S., Youssef, E.S.M.: Solving fractional integro-differential equations by using Sumudu transform method and Hermite spectral collocation method. CMC Comput. Mater. Continua 54(2), 161–180 (2018)
Arikoglu, A., Ozkol, I.: Solution of fractional integro-differential equations by using fractional differential transform method. Chaos Solitons Fractals 40(2), 521–529 (2009)
Bakaev, N.Y., Larsson, S., Thomée, V.: Euler, backward, type methods for parabolic integro-differential equations in Banach space. RAIRO Modél. Math. Anal. Numér. 32(1), 85–99 (1998)
Balachandran, K., Trujillo, J.J.: The nonlocal Cauchy problem for nonlinear fractional integrodifferential equations in Banach spaces. Nonlinear Anal. 72(12), 4587–4593 (2010)
Bazhlekova, E., Jin, B., Lazarov, R., Zhou, Z.: An analysis of the Rayleigh–Stokes problem for a generalized second-grade fluid. Numer. Math. 131(1), 1–31 (2015)
Cannon, J.R., Lin, Y.: Nonclassical \(H^1\) projection and Galerkin methods for nonlinear parabolic integro-differential equations. Calcolo 25(3), 187–201 (1988)
Chen, C., Shih, T.: Finite Element Methods for Integrodifferential Equations, vol. 9. World Scientific, River Edge (1998)
Cuesta, E., Lubich, C., Palencia, C.: Convolution quadrature time discretization of fractional diffusion-wave equations. Math. Comput. 75(254), 673–696 (2006)
El-Borai, M.M., El-Nadi, K.E.S., Ahmed, H.M., El-Owaidy, H.M., Ghanem, A.S., Sakthivel, R.: Existence and stability for fractional parabolic integro-partial differential equations with fractional Brownian motion and nonlocal condition. Cogent Math. Stat. 5(1), 1460030 (2018)
Ern, A., Guermond, J.-L.: Theory and Practice of Finite Elements, vol. 159. Springer, New York (2004)
Fujita, H., Suzuki, T.: Evolution problems. In: Handbook of Numerical Analysis, vol. II, Handb. Numer. Anal., II, pp. 789–928. North-Holland, Amsterdam (1991)
Hecht, F.: New development in freefem++. J. Numer. Math. 20(3–4), 251–265 (2012)
Hu, L., Ren, Y., Sakthivel, R.: Existence and uniqueness of mild solutions for semilinear integro-differential equations of fractional order with nonlocal initial conditions and delays. Semigr. Forum 79(3), 507–514 (2009)
Huang, L., Li, X.-F., Zhao, Y., Duan, X.-Y.: Approximate solution of fractional integro-differential equations by Taylor expansion method. Comput. Math. Appl. 62(3), 1127–1134 (2011)
Jin, B., Lazarov, R., Zhou, Z.: Error estimates for a semidiscrete finite element method for fractional order parabolic equations. SIAM. J. Numer. Anal 51(1), 445–466 (2013)
Jin, B., Lazarov, R., Zhou, Z.: Two fully discrete schemes for fractional diffusion and diffusion-wave equations with nonsmooth data. SIAM. J. Sci. Comput. 38(1), A146–A170 (2016)
Jin, B., Li, B., Zhou, Z.: An analysis of the Crank–Nicolson method for subdiffusion. IMA J. Numer. Anal. 38(1), 518–541 (2018)
Karaa, S., Mustapha, K., Pani, A.K.: Optimal error analysis of a FEM for fractional diffusion problems by energy arguments. J. Sci. Comput. 74(1), 519–535 (2018)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier, Amsterdam (2006)
Lin, Y., Thomée, V., Wahlbin, L.B.: Ritz–Volterra projections to finite-element spaces and applications to integrodifferential and related equations. SIAM. J. Numer. Anal. 28(4), 1047–1070 (1991)
Lubich, C.: Discretized fractional calculus. SIAM. J. Math. Anal. 17(3), 704–719 (1986)
Lubich, C.: Convolution quadrature and discretized operational calculus. I. Numer. Math. 52(2), 129–145 (1988)
Lubich, C.: Convolution quadrature revisited. BIT 44(3), 503–514 (2004)
Lubich, C., Sloan, I.H., Thomée, V.: Nonsmooth data error estimates for approximations of an evolution equation with a positive-type memory term. Math. Comput. 65(213), 1–17 (1996)
Ma, X., Huang, C.: Numerical solution of fractional integro-differential equations by a hybrid collocation method. Appl. Math. Comput. 219(12), 6750–6760 (2013)
Mahata, S., Sinha, R.K.: On the existence, uniqueness and stability results for time-fractional parabolic integro-differential equations. J. Integral Equ. Appl. 32(4), 457–477 (2020)
Maleknejad, K., Sahlan, M.N., Ostadi, A.: Numerical solution of fractional integro-differential equation by using cubic B-spline wavelets. In: Proceedings of the World Congress on Engineering, vol. 1 (2013)
Mohammed, D.S.: Numerical solution of fractional integro-differential equations by least squares method and shifted Chebyshev polynomial. Math. Probl. Eng. Art. ID 431965, 5 (2014)
Momani, S., Noor, M.A.: Numerical methods for fourth-order fractional integro-differential equations. Appl. Math. Comput. 182(1), 754–760 (2006)
Mustapha, K.: FEM for time-fractional diffusion equations, novel optimal error analyses. Math. Comput. 87(313), 2259–2272 (2018)
Oyedepo, T., Taiwo, O.A., Abubakar, J.U., Ogunwobi, Z.O.: Numerical studies for solving fractional integro-differential equations by using least squares method and Bernstein polynomials. Fluid Mech. Open Access 3(3), 1000142 (2016)
Podlubny, I.: Fractional Differential Equations, vol. 198. Academic Press, San Diego (1999)
Qiao, L., Wang, Z., Xu, D.: An alternating direction implicit orthogonal spline collocation method for the two dimensional multi-term time fractional integro-differential equation. Appl. Numer. Math. 151, 199–212 (2020)
Qiu, W., Xu, D., Chen, H.: A formally second-order BDF finite difference scheme for the integro-differential equations with the multi-term kernels. Int. J. Comput. Math. 97(10), 2055–2073 (2020)
Rawashdeh, E.A.: Numerical solution of fractional integro-differential equations by collocation method. Appl. Math. Comput. 176(1), 1–6 (2006)
Saadatmandi, A., Dehghan, M.: A Legendre collocation method for fractional integro-differential equations. J. Vib. Control 17(13), 2050–2058 (2011)
Sanz-Serna, J.M.: A numerical method for a partial integro-differential equation. SIAM J. Numer. Anal. 25(2), 319–327 (1988)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems, vol. 25. Springer, Berlin (2006)
Thomée, V., Zhang, N.-Y.: Error estimates for semidiscrete finite element methods for parabolic integro-differential equations. Math. Comput. 53(187), 121–139 (1989)
Unhale, S.I., Kendre, S.D.: Numerical solution of nonlinear fractional integro-differential equation by collocation method, 2018. Malaya J. Mat. 6(1), 73–79 (2018)
Zaeri, S., Saeedi, H., Izadi, M.: Fractional integration operator for numerical solution of the integro-partial time fractional diffusion heat equation with weakly singular kernel. Asian-Eur. J. Math. 10(04), 1750071 (2017)
Zhou, J., Xu, D.: Alternating direction implicit difference scheme for the multi-term time-fractional integro-differential equation with a weakly singular kernel. Comput. Math. Appl. 79(2), 244–255 (2020)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Mahata, S., Sinha, R.K. Finite Element Method for Fractional Parabolic Integro-Differential Equations with Smooth and Nonsmooth Initial Data. J Sci Comput 87, 7 (2021). https://doi.org/10.1007/s10915-021-01412-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-021-01412-3
Keywords
- Fractional parabolic integro-differential equation
- Finite element method
- Semidiscrete
- Fully discrete
- Smooth and nonsmooth initial data
- Convolution quadrature
- Error estimates