Skip to main content
Springer Nature Link
Log in

A Multigrid Algorithm for Maxflow and Min-Cut Problems with Applications to Multiphase Image Segmentation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

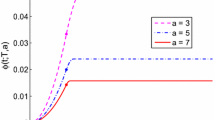
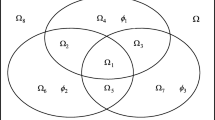
Abstract

In this paper, we propose a multiphase image segmentation method via solving the min-cut minimization problem under the multigrid method framework. At each level of the multigrid method for the min-cut problem, we first transfer it to the equivalent form, e.g., max-flow problem, then actually solve the dual of the max-flow problem. Particularly, a classical multigrid method is used to solve the sub-minimization problems. Several outer iterations are used for the multigrid method. The proposed idea can be used for general min-cut/max-flow minimization problems. We use multiphase image segmentation as an example in this work. Extensive experiments on simulated and real images demonstrate the efficiency and effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. The models used in the FCM-L1 and SLaT methods are different, thus it is not meaningful to discuss the energy change.

References

  1. Pock, T., Antonin, C., Cremers, E., Bischof, H.: A convex relaxation approach for computing minimal partitions. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2019)

  2. Li, F., Osher, S., Qin, J., Yan, M.: A multiphase image segmentation based on fuzzy membership functions and L1-norm fidelity. J. Sci. Comput. 69, 82–106 (2016)

    Article  MathSciNet  Google Scholar 

  3. Chan, R., Yang, H., Zeng, T.: A two-stage image segmentation method for blurry images with Poisson or multiplicative gamma noise. SIAM J. Imaging Sci. 7(1), 98–127 (2014)

    Article  MathSciNet  Google Scholar 

  4. Chan, R., Lanza, A., Morigi, S., Sgallari, F.: Convex non-convex image segmentation. Numerische Mathematik 138(3), 635–680 (2018)

    Article  MathSciNet  Google Scholar 

  5. Cai, X., Chan, R., Zeng, T.: A two-stage image segmentation method using a convex variant of the Mumford–Shah model and thresholding. SIAM J. Imaging Sci. 6(1), 368–390 (2013)

    Article  MathSciNet  Google Scholar 

  6. Cai, X., Chan, R., Morigi, S., Sgallazi, F.: Vessel segmentation in medical imaging using a tight-frame based algorithm. SIAM J. Imaging Sci. 6(1), 464–486 (2013)

    Article  MathSciNet  Google Scholar 

  7. Cai, X., Chan, R., Schonlieb, C.-B., Steidl, G., Zeng, T.: Linkage between piecewise constant Mumford–Shah model and Rudin–Osher–Fatemi model and its virtue in image segmentation. SIAM J. Sci. Comput. 41(6), B1310–B1340 (2019)

    Article  MathSciNet  Google Scholar 

  8. Tan, L., Pan, Z., Liu, W., Duan, J., Wei, W., Wang, G.: Image segmentation with depth information via simplified variational level set formulation. J. Math. Imaging Vis. 60, 1–17 (2018)

    Article  MathSciNet  Google Scholar 

  9. Spencer, J., Chen, K., Duan, J.: Parameter-free selective segmentation with convex variational methods. IEEE Trans. Image Process. 28(5), 2163–2172 (2019)

    Article  MathSciNet  Google Scholar 

  10. Mumford, D., Shah, J.: Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 42, 577–685 (1989)

    Article  MathSciNet  Google Scholar 

  11. Zhu, S., Yuille, A.: Region competition: unifying snakes, region growing, and Bayes/MDL for multiband image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 18, 884–900 (1996)

    Article  Google Scholar 

  12. Chan, T.F., Vese, L.A.: Active contours without edges. IEEE Trans. Image Process. 10, 266–277 (2001)

    Article  Google Scholar 

  13. Osher, S., Sethian, J.: Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 79, 12–49 (1988)

    Article  MathSciNet  Google Scholar 

  14. Aubert, G., Kornprobst, P.: Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations, Vol. 147. Springer (2006)

  15. Caselles, V., Kimmel, R., Sapiro, G.: Geodesic active contours. Int. J. Comput. Vis. 22, 61–79 (1997)

    Article  Google Scholar 

  16. Guo, W., Qin, J., Tari, S.: Automatic prior shape selection for image segmentation. Res. Shape Model. (2015)

  17. Tan, L., Pan, Z., Liu, W., Duan, J., Wei, W., Wang, G.: Image segmentation with depth information via simplified variational level set formulation. J. Math. Imaging Vis. 60(1), 1–17 (2018)

    Article  MathSciNet  Google Scholar 

  18. Bresson, X., Esedoglu, S., Vandergheynst, P., Thiran, J.-P., Osher, S.: Fast global minimization of the active contour/snake model. J. Math. Imaging Vis. 28, 151–167 (2007)

    Article  MathSciNet  Google Scholar 

  19. Houhou, N., Thiran, J., Bresson, X.: Fast texture segmentation model based on the shape operator and active contour. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1–8 (2008)

  20. Mory, B., Ardon, R.: Fuzzy region competition: a convex two-phase segmentation framework. In: Scale Space and Variational Methods in Computer Vision, pp. 214–226. Springer (2007)

  21. Lie, J., Lysaker, M., Tai, X.-C.: A binary level set model and some applications to Mumford–Shah image segmentation. IEEE Trans. Image Process. 15, 1171–1181 (2006)

    Article  Google Scholar 

  22. Chan, T., Esedoglu, S., Nikolova, M.: Algorithms for finding global minimizers of image segmentation and denoising models. SIAM J. Appl. Math. 66, 1632–1648 (2006)

    Article  MathSciNet  Google Scholar 

  23. Chambolle, Antonin, Cremers, D., Pock, T.: A convex approach to minimal partitions. SIAM J. Imaging Sci. 5(4), 1113–1158 (2012)

    Article  MathSciNet  Google Scholar 

  24. Yuan, J., Bae, E., Tai, X.-C.: A study on continuous max-flow and min-cut approaches. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2010)

  25. Yuan, J., Bae, E., Tai, X.-C., Boykov, Y.: A continuous max-flow approach to Potts model. In: European Conference on Computer Vision (ECCV), pp. 379–392 (2010)

  26. Bae, E., Yuan, J., Tai, X.-C., Boykov, T.: A fast continuous max-flow approach to non-convex multilabeling problems. In: Efficient Global Minimization Methods for Variational Problems in Imaging and Vision (2011)

  27. Yuan, J., Bae, E., Tai, X.-C., Boykov, Y.: A spatially continuous max-flow and min-cut framework for binary labeling problems. Numerische Mathematik 66, 1–29 (2013)

    MATH  Google Scholar 

  28. Bae, E., Lellmann, J., Tai, X.-C.: Convex relaxations for a generalized Chan–Vese model. In: Energy Minimization Methods in Computer Vision and Pattern Recognition, pp. 223–236. Springer (2013)

  29. Bae, E., Tai, X.-C.: Efficient global minimization methods for image segmentation models with four regions. J. Math. Imaging Vis. 51, 71–97 (2015)

    Article  MathSciNet  Google Scholar 

  30. Briggs, W., Henson, V., McCormick, S.: A Multigrid Tutorial. SIAM, Philadelphia (2000)

    Book  Google Scholar 

  31. Donatelli, M.: A multigrid for image deblurring with Tikhonov regularization. Numer. Linear Algebra Appl. 12, 715–729 (2005)

    Article  MathSciNet  Google Scholar 

  32. Chen, K., Tai, X.-C.: A nonlinear multigrid method for total variation minimization from image restoration. J. Sci. Comput. 33, 115–138 (2007)

    Article  MathSciNet  Google Scholar 

  33. Español, M.: Multilevel Methods for Discrete Ill-Posed Problems: Application to Deblurring, PhD thesis, Department of Mathematicsm, Tufts University (2009)

  34. Español, M., Kilmer, M.: Multilevel approach for signal restoration problems with Toeplitz matrices. SIAM J. Sci. Comput. 32, 299–319 (2010)

    Article  MathSciNet  Google Scholar 

  35. Chen, K., Dong, Y., Hintermüller, M.: A nonlinear multigrid solver with line Gauss–Seidel–Semismooth–Newton smoother for the Fenchel predual in total variation based image restoration. Inverse Probl. Imaging 5, 323–339 (2011)

    Article  MathSciNet  Google Scholar 

  36. Deng, L.-J., Huang, T.-Z., Zhao, X.-L.: Wavelet-based two-level methods for image restoration. Commun. Nonlinear Sci. Numer. Simul. 17, 5079–5087 (2012)

    Article  MathSciNet  Google Scholar 

  37. Chumchob, N., Chen, K.: A robust multigrid approach for variational image registration models. J. Comput. Appl. Math. 236, 653–674 (2011)

    Article  MathSciNet  Google Scholar 

  38. Badshah, N., Chen, K.: Multigrid method for the Chan–Vese model in variational segmentation. Commun. Comput. Phys 4, 294–316 (2008)

    MathSciNet  MATH  Google Scholar 

  39. Badshah, N., Chen, K.: On two multigrid algorithms for modeling variational multiphase image segmentation. IEEE Trans. Image Process. 18, 1097–1106 (2009)

    Article  MathSciNet  Google Scholar 

  40. Deng, L.-J., Huang, T.-Z., Zhao, X.-L., Zhao, L., Wang, S.: Signal restoration combining Tikhonov regularization and multilevel method with thresholding strategy. J. Opt. Soc. Am. Opt. Image Sci. Vis. 30, 948–955 (2013)

    Article  Google Scholar 

  41. Yuan, J., Bae, E., Tai, X.-C., Boykov, T.: “A study on continuous max-flow and min-cut approaches”, Technical report CAM10-61. UCLA, CAM (2010)

  42. Wei, K., Yin, K., Tai, X.-C., Chan, T.F.: New region force for variational models in image segmentation and high dimensional data clustering. Ann. Math. Sci. Appl. 3(1), 255–286 (2018)

    MathSciNet  MATH  Google Scholar 

  43. Ishikawa, Hiroshi: Exact optimization for Markov random fields with convex priors. IEEE Trans. Pattern Anal. Mach. Intell. 25, 1333–1336 (2003)

    Article  Google Scholar 

  44. Darbon, J., Sigelle, M.: Image restoration with constrained total variation. Part II: levelable functions, convex priors and non-convex cases. J. Math. Imaging Vis. 26(3), 277–292 (2006)

    Article  Google Scholar 

  45. Darbon, J., Sigelle, M.: Image restoration with discrete constrained total variation part I: fast and exact optimization. J. Math. Imaging Vis. 26(3), 261–276 (2006)

    Article  Google Scholar 

  46. Bae, E., Yuan, J., Tai, X.-C., Boykov, Y.: A fast continuous max-flow approach to non-convex multi-labeling problems. In: Efficient Algorithms for Global Optimization Methods in Computer Vision, pp. 134–154. Springer (2014)

  47. Goldluecke, Bastian, Cremers, D.: Convex relaxation for multilabel problems with product label spaces. Comput. Vis. ECCV 2010, 225–238 (2010)

    Google Scholar 

  48. Vese, L.A., Chan, T.F.: A new multiphase level set framework for image segmentation via the Mumford and Shah model. Int. J. Comput. Vis. 50, 271–293 (2002)

    Article  Google Scholar 

  49. Kiefer, J.: Sequential minimax search for a maximum. Proc. Am. Math. Soc. 4, 502–506 (1953)

    Article  MathSciNet  Google Scholar 

  50. Condat, Laurent: Fast projection onto the simplex and the l1 ball. Math. Program. 158(1–2), 575–585 (2016)

    Article  MathSciNet  Google Scholar 

  51. Chen, Y., Ye, X.: Projection onto a simplex. arXiv preprint arXiv:1101.6081 (2011)

  52. Cai, X., Chan, R., Nikolova, M., Zeng, T.: A three-stage approach for segmenting degraded color images: smoothing, lifting and thresholding (SLaT). J. Sci. Comput. 72(3), 1313–1332 (2017)

    Article  MathSciNet  Google Scholar 

  53. Yin, K., Tai, X.-C.: An effective region force for some variational models for learning and clustering. J. Sci. Comput. 74, 175–196 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work of Xue-Cheng Tai was supported by RG(R)-RC/17-18/02-MATH, HKBU 12300819, NSF/RGC Grant N-HKBU214-19 and RC-FNRA-IG/19-20/SCI/01. The work of Liang-Jian Deng was partially supported by National Natural Science Foundation of China Grants 61702083, 61772003 and Key Projects of Applied Basic Research in Sichuan Province Grants 2020YJ0216. Besides, the work of Ke Yin was supported by National Natural Science Foundation of China Grant 11801200.

Author information

Authors and Affiliations

  1. Department of Mathematics, Hong Kong Baptist University, Kowloon Tsai, Hong Kong

    Xue-Cheng Tai

  2. School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, China

    Liang-Jian Deng

  3. Center for Mathematical Sciences, Huazhong University of Science and Technology, Wuhan, China

    Ke Yin

Authors
  1. Xue-Cheng Tai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Liang-Jian Deng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ke Yin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Liang-Jian Deng.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tai, XC., Deng, LJ. & Yin, K. A Multigrid Algorithm for Maxflow and Min-Cut Problems with Applications to Multiphase Image Segmentation. J Sci Comput 87, 101 (2021). https://doi.org/10.1007/s10915-021-01458-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-021-01458-3

Keywords