Skip to main content
Springer Nature Link
Log in

Weighted Hyper-Laplacian Prior with Overlapping Group Sparsity for Image Restoration under Cauchy Noise

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

In this paper, we deal with the Cauchy image restoration problem under the maximum a posteriori framework. We propose a novel image prior, weighted hyper-Laplacian prior with overlapping group sparsity on the image gradient. This prior allows us to simultaneously promote the structural and pixel-level sparseness of the natural image gradient. The performance can be further improved by introducing the in-group-weights to balance the different scales of the components within each group. To tackle the corresponding optimization problem, we present a novel quadratic majorizer for majorization-minimization. We adopt the non-convex alternating direction method of multipliers as the main algorithm framework. The proposed regularizer can be reduced to the related variational regularizers including the total variation, the hyper-Laplacian, and the total variation with overlapping group sparsity. The comparative experiments with those existing gradient-based regularizers demonstrate the effectiveness of the proposed method in terms of PSNR and SSIM values.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Notes

  1. The detailed derivation is shown in the supplementary material.

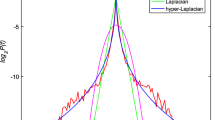
  2. The plots for the “parrot” and “jellyfish” images can be found in the supplementary material.

References

  1. Al-Aboosi, Y.Y., Bin Sha’ameri, A.Z., Khamis, N.H.H.: Comparison of methodologies for signal detection in underwater acoustic noise in shallow tropical waters. ARPN J. Eng. Appl. Sci. 11(5), 3086–3094 (2016)

    Google Scholar 

  2. Antoniadis, A., Leporini, D., Pesquet, J.C.: Wavelet thresholding for some classes of non-Gaussian noise. Stat. Neerlandica 56(4), 434–453 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  3. Arikan, O., Belge, M., Cetin, A.E., Erzin, E.: Adaptive filtering approaches for non-Gaussian stable processes. In: 1995 International Conference on Acoustics, Speech, and Signal Processing, vol. 2, IEEE, pp. 1400–1403 (1995)

  4. Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Math. Program. 137(1–2), 91–129 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Banerjee, S., Agrawal, M.: Underwater acoustic communication in the presence of heavy-tailed impulsive noise with bi-parameter Cauchy–Gaussian mixture model. In: 2013 Ocean Electronics (SYMPOL), IEEE, pp. 1–7 (2013)

  6. Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1–2), 459–494 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  7. Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  8. Carrillo, R.E., Aysal, T.C., Barner, K.E.: A generalized Cauchy distribution framework for problems requiring robust behavior. EURASIP J. Adv. Signal Process. 2010(1), 312989 (2010)

    Article  Google Scholar 

  9. Chan, R.H., Dong, Y., Hintermuller, M.: An efficient two-phase method for restoring blurred images with impulse noise. IEEE Trans. Image Process. 19(7), 1731–1739 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chan, R.H., Tao, M., Yuan, X.: Constrained total variation deblurring models and fast algorithms based on alternating direction method of multipliers. SIAM J. Imaging Sci. 6(1), 680–697 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chan, T., Marquina, A., Mulet, P.: High-order total variation-based image restoration. SIAM J. Sci. Comput. 22(2), 503–516 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  12. Chang, Y.C., Kadaba, S.R., Doerschuk, P.C., Gelfand, S.B.: Image restoration using recursive Markov random field models driven by Cauchy distributed noise. IEEE Signal Process. Lett. 8(3), 65–66 (2001)

    Article  Google Scholar 

  13. Cheng, J., Gao, Y., Guo, B., Zuo, W.: Image restoration using spatially variant hyper-Laplacian prior. SIViP 13(1), 155–162 (2019a)

    Article  Google Scholar 

  14. Cheng, M.H., Huang, T.Z., Zhao, X.L., Ma, T.H., Huang, J.: A variational model with hybrid hyper-Laplacian priors for Retinex. Appl. Math. Model. 66, 305–321 (2019b)

    Article  MathSciNet  MATH  Google Scholar 

  15. Chitre, M.A., Potter, J.R., Ong, S.H.: Optimal and near-optimal signal detection in snapping shrimp dominated ambient noise. IEEE J. Oceanic Eng. 31(2), 497–503 (2006)

    Article  Google Scholar 

  16. Chuan, H., Chang-Hua, H., Zhang, W., Biao, S.: Box-constrained total-variation image restoration with automatic parameter estimation. Acta Automatica Sinica 40(8), 1804–1811 (2014)

    Article  Google Scholar 

  17. Deng, L.J., Feng, M., Tai, X.C.: The fusion of panchromatic and multispectral remote sensing images via tensor-based sparse modeling and hyper-Laplacian prior. Inf. Fusion 52, 76–89 (2019)

    Article  Google Scholar 

  18. Ding, M., Huang, T.Z., Ma, T.H., Zhao, X.L., Yang, J.H.: Cauchy noise removal using group-based low-rank prior. Appl. Math. Comput. 372, 124971 (2020)

    MathSciNet  MATH  Google Scholar 

  19. Ding, M., Huang, T.Z., Wang, S., Mei, J.J., Zhao, X.L.: Total variation with overlapping group sparsity for deblurring images under Cauchy noise. Appl. Math. Comput. 341, 128–147 (2019)

    MathSciNet  MATH  Google Scholar 

  20. Dong, Y., Xu, S.: A new directional weighted median filter for removal of random-valued impulse noise. IEEE Signal Process. Lett. 14(3), 193–196 (2007)

    Article  Google Scholar 

  21. El Ghannudi, H., Clavier, L., Azzaoui, N., Septier, F., Rolland, P.A.: \(\alpha \)-stable interference modeling and Cauchy receiver for an IR-UWB ad hoc network. IEEE Trans. Commun. 58(6), 1748–1757 (2010)

    Article  Google Scholar 

  22. Fergus, R., Singh, B., Hertzmann, A., Roweis, S.T., Freeman, W.T.: Removing camera shake from a single photograph. ACM Trans. Graph. 25(3), 787–794 (2006)

    Article  MATH  Google Scholar 

  23. Figueiredo, M.A., Bioucas-Dias, J.M., Nowak, R.D.: Majorization-minimization algorithms for Wavelet-based image restoration. IEEE Trans. Image Process. 16(12), 2980–2991 (2007)

    Article  MathSciNet  Google Scholar 

  24. Gu, S., Zhang, L., Zuo, W., Feng, X.: Weighted nuclear norm minimization with application to image denoising. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 2862–2869 (2014)

  25. Gurugopinath, S., Muralishankar, R., Shankar, H.: Spectrum sensing in the presence of Cauchy noise through differential entropy. In: 2016 IEEE Distributed Computing, VLSI, Electrical Circuits and Robotics (DISCOVER), IEEE, pp. 201–204 (2016)

  26. Hansen, P.C., Nagy, J.G., O’leary, D.P.: Deblurring images: matrices, spectra, and filtering, vol. 3. SIAM (2006)

  27. Hasannasab, M., Hertrich, J., Laus, F., Steidl, G.: Alternatives to the EM algorithm for ML estimation of location, scatter matrix, and degree of freedom of the Student t-distribution. In: Numerical Algorithms pp. 1–42 (2020)

  28. Hong, M., Luo, Z.Q., Razaviyayn, M.: Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM J. Optim. 26(1), 337–364 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  29. Hongbo, Z., Liuyan, R., Lingling, K., Xujia, Q., Meiyu, Z.: Single image fast deblurring algorithm based on hyper-Laplacian model. IET Image Proc. 13(3), 483–490 (2018)

    Article  Google Scholar 

  30. Hunter, D.R., Lange, K.: A tutorial on MM algorithms. Am. Stat. 58(1), 30–37 (2004)

    Article  MathSciNet  Google Scholar 

  31. Idan, M., Speyer, J.L.: Cauchy estimation for linear scalar systems. IEEE Trans. Autom. Control 55(6), 1329–1342 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  32. Karayiannis, N.B., Venetsanopoulos, A.N.: Regularization theory in image restoration-the stabilizing functional approach. IEEE Trans. Acoust. Speech Signal Process. 38(7), 1155–1179 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  33. Kim, G., Cho, J., Kang, M.: Cauchy noise removal by weighted nuclear norm minimization. J. Sci. Comput. 83(1), 15 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Kong, J., Lu, K., Jiang, M.: A new blind deblurring method via hyper-Laplacian prior. Procedia Comput. Sci. 107, 789–795 (2017)

    Article  Google Scholar 

  35. Krishnan, D., Fergus, R.: Fast image deconvolution using hyper-Laplacian priors. In: Advances in Neural Information Processing Systems, pp. 1033–1041 (2009)

  36. Kumar, A., Ahmad, M.O., Swamy, M.: An efficient denoising framework using weighted overlapping group sparsity. Inf. Sci. 454, 292–311 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  37. Kwitt, R., Meerwald, P., Uhl, A.: A lightweight Rao–Cauchy detector for additive watermarking in the DWT-domain. In: Proceedings of the 10th ACM workshop on Multimedia and Security, pp. 33–42 (2008)

  38. Laus, F., Pierre, F., Steidl, G.: Nonlocal myriad filters for Cauchy noise removal. J. Math. Imaging Vis. 60(8), 1324–1354 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  39. Lee, S., Kang, M.: Group sparse representation for restoring blurred images with Cauchy noise. J. Sci. Comput. 83(3) (2020)

  40. Levin, A., Fergus, R., Durand, F., Freeman, W.T.: Image and depth from a conventional camera with a coded aperture. ACM Trans. Gr. (TOG) 26(3), 70 (2007)

    Article  Google Scholar 

  41. Levin, A., Weiss, Y., Durand, F., Freeman, W.T.: Understanding and evaluating blind deconvolution algorithms. In: IEEE Conference on Computer Vision and Pattern Recognition, IEEE, pp. 1964–1971 (2009)

  42. Li, G., Pong, T.K.: Global convergence of splitting methods for nonconvex composite optimization. SIAM J. Optim. 25(4), 2434–2460 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  43. Lin, T., Ma, S., Zhang, S.: Global convergence of unmodified 3-block ADMM for a class of convex minimization problems. J. Sci. Comput. 76(1), 69–88 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  44. Liu, J., Huang, T.Z., Liu, G., Wang, S., Lv, X.G.: Total variation with overlapping group sparsity for speckle noise reduction. Neurocomputing 216, 502–513 (2016)

    Article  Google Scholar 

  45. Liu, J., Huang, T.Z., Selesnick, I.W., Lv, X.G., Chen, P.Y.: Image restoration using total variation with overlapping group sparsity. Inf. Sci. 295, 232–246 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  46. Liu, J., Yan, M., Zeng, T.: Surface-aware blind image deblurring. IEEE Trans. Pattern Anal. Mach. Intell. (2019)

  47. Liu, P., Zhang, H., Zhang, K., Lin, L., Zuo, W.: Multi-level wavelet-CNN for image restoration. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), pp. 886–88609 (2018)

  48. Mei, J.J., Dong, Y., Huang, T.Z., Yin, W.: Cauchy noise removal by nonconvex ADMM with convergence guarantees. J. Sci. Comput. 74(2), 743–766 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  49. Pan, J., Hu, Z., Su, Z., Yang, M.H.: Deblurring face images with exemplars. In: European Conference on Computer Vision, Springer, pp. 47–62 (2014)

  50. Parizi, S.N., He, K., Aghajani, R., Sclaroff, S., Felzenszwalb, P.F.: Generalized majorization-minimization. In: International Conference on Machine Learning, pp. 5022–5031 (2019)

  51. Peng, Y., Chen, J., Xu, X., Pu, F.: SAR images statistical modeling and classification based on the mixture of alpha-stable distributions. Remote Sens. 5(5), 2145–2163 (2013)

    Article  Google Scholar 

  52. Rebegoldi, S., Bonettini, S., Prato, M.: Efficient block coordinate methods for blind cauchy denoising. In: International Conference on Numerical Computations: Theory and Algorithms, Springer, pp. 198–211 (2019)

  53. Sciacchitano, F., Dong, Y., Zeng, T.: Variational approach for restoring blurred images with Cauchy noise. SIAM J. Imaging Sci. 8(3), 1894–1922 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  54. Selesnick, I.W., Chen, P.Y.: Total variation denoising with overlapping group sparsity. In: IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, pp. 5696–5700 (2013)

  55. Shi, M., Han, T., Liu, S.: Total variation image restoration using hyper-Laplacian prior with overlapping group sparsity. Sig. Process. 126, 65–76 (2016)

    Article  Google Scholar 

  56. Tsihrintzis, G., Tsakalides, P., Nikias, C.: Signal detection in severely heavy-tailed radar clutter. In: Conference Record of The Twenty-Ninth Asilomar Conference on Signals, Systems and Computers, vol. 2, IEEE, pp. 865–869 (1995)

  57. Wang, Y., Yin, W., Zeng, J.: Global convergence of ADMM in nonconvex nonsmooth optimization. J. Sci. Comput. 78(1), 29–63 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  58. Wu, T., Li, W., Jia, S., Dong, Y., Zeng, T.: Deep multi-level Wavelet-CNN denoiser prior for restoring blurred image with Cauchy noise. IEEE Signal Process. Lett. 27, 1635–1639 (2020)

    Article  Google Scholar 

  59. Xu, X., Pan, J., Zhang, Y.J., Yang, M.H.: Motion blur kernel estimation via deep learning. IEEE Trans. Image Process. 27(1), 194–205 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  60. Xu, Y., Yin, W.: A block coordinate descent method for regularized multiconvex optimization with applications to nonnegative tensor factorization and completion. SIAM J. Imaging Sci. 6(3), 1758–1789 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  61. Yang, J.H., Zhao, X.L., Mei, J.J., Wang, S., Ma, T.H., Huang, T.Z.: Total variation and high-order total variation adaptive model for restoring blurred images with Cauchy noise. Comput. Math. Appl. 77(5), 1255–1272 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  62. Zimmermann, M., Dostert, K.: Analysis and modeling of impulsive noise in broad-band powerline communications. IEEE Trans. Electromagn. Compat. 44(1), 249–258 (2002)

    Article  Google Scholar 

  63. Zuo, W., Ren, D., Gu, S., Lin, L., Zhang, L.: Discriminative learning of iteration-wise priors for blind deconvolution. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 3232–3240 (2015)

Download references

Acknowledgements

This work is supported in part by the National Natural Science Foundation of China (Nos. 11771072, 11701079, 61806024); the Science and Technology Development Plan of Jilin Province (Nos. 20191008004TC, 20180520026JH); Jilin Provincial Department of Education (JJKH20190293KJ); the Fundamental Research Funds for the Central Universities (Nos. 2412019FZ030, 2412020FZ023).

Author information

Authors and Affiliations

  1. Key Laboratory for Applied Statistics of MOE, School of Mathematics and Statistics, Northeast Normal University, Changchun, 130024, People’s Republic of China

    Kyongson Jon, Jun Liu, Xiaofei Wang, Wensheng Zhu & Yu Xing

  2. Faculty of Mathematics, Kim Il Sung University, Pyongyang, 999093, Democratic People’s Republic of Korea

    Kyongson Jon

Authors
  1. Kyongson Jon
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jun Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xiaofei Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Wensheng Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Yu Xing
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Wensheng Zhu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 372 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jon, K., Liu, J., Wang, X. et al. Weighted Hyper-Laplacian Prior with Overlapping Group Sparsity for Image Restoration under Cauchy Noise. J Sci Comput 87, 64 (2021). https://doi.org/10.1007/s10915-021-01461-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-021-01461-8

Keywords