Preasymptotic Error Analysis of the HDG Method for Helmholtz Equation with Large Wave Number

Abstract

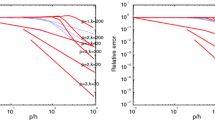
This paper addresses several aspects of the linear hybridizable discontinuous Galerkin method (HDG) for the Helmholtz equation with impedance boundary condition at high frequency. First, error estimates with explicit dependence on the wave number k for the HDG approximations to the exact solution u and its negative gradient ${\mathbf {q}}=-\nabla u$ are derived. It is shown that $k\Vert u-u_h\Vert _{L^2(\varOmega )}+ \Vert {\mathbf {q}}-{\mathbf {q}}_h\Vert _{L^2(\varOmega )}=O(k^2h^2+k^4h^3)$ under the conditions that $k^3h^2$ is sufficiently small and that the penalty parameter $\tau \eqsim k$, where h is the mesh size. Note that the convergence order in ${\mathbf {q}}_h$ is full and the pollution error is $O(k^4h^3)$, which improve the existent results. Secondly, by using a standard postprocessing procedure from the HDG method for elliptic problems, a piecewise quadratic function $u_h^*$ is obtained so that $k\Vert u-u_h^*\Vert _{L^2(\varOmega )}=O(k^3h^3+k^4h^3)$. Note that the postprocessing procedure improves only the interpolation error (from $O(k^2h^2)$ to $O(k^3h^3)$) but leaves the pollution error $O(k^4h^3)$ unchanged. Thirdly, a dispersion analysis and extensive numerical tests show that the pollution effect can be reduced greatly in 2D case by selecting appropriate penalty parameters.