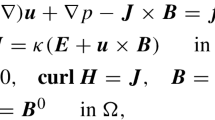Skip to main content
Springer Nature Link
Log in

Error Estimate of a Fully Discrete Finite Element Method for Incompressible Vector Potential Magnetohydrodynamic System

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

We investigate a fully discrete finite element scheme for the three-dimensional incompressible magnetohydrodynamic problem based on magnetic vector potential formulation that was introduced in Hiptmair et al. (MMMAS 28:659–695, 2018). The formulation enjoys the novel feature that it can always produce an exactly divergence-free magnetic induction discretized solution. Using a mixed finite element approach, we discretize the model by the fully discrete semi-implicit Euler scheme with the velocity and the pressure approximated by stable MINI finite elements and the magnetic vector potential by Nédélec edge elements. Under a reasonable regularity hypothesis for the exact solution, error estimates for the velocity and the magnetic vector potential are rigorously established. Finally, several numerical experiments are presented to illustrate the convergence properties of the numerical scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Biskamp, D.: Nonlinear magnetohydrodynamics. Cambridge Monographs on Plasma Physics. 1. Cambridge University Press, Cambridge (1993)

  2. Boffi, D.: Fortin operator and discrete compactness for edge elements. Numer. Math. 87, 229–246 (2000)

    Article  MathSciNet  Google Scholar 

  3. Boffi, D., Brezzi, F., Fortin, M.: Mixed finite element methods and applications. Springer Series in Computational Mathematics, 44. Springer, Heidelberg (2013)

  4. Brackbill, J.U., Barnes, D.C.: The effect of nonzero \(\nabla \cdot { B}\) on the numerical solution of the magnetohydrodynamic equations. J. Comput. Phys. 35, 426–430 (1980)

    Article  MathSciNet  Google Scholar 

  5. Brenner, S.C., Scott, L.R.: The mathematical theory of finite element methods. Texts in Applied Mathematics, 15. Springer-Verlag, New York (1994)

  6. Brenner, S.C., Scott, L.R.: The mathematical theory of finite element methods. Texts in Applied Mathematics. 15, 3rd edn. Springer, New York (2008)

  7. Brezzi, F., Fortin, M.: Mixed and hybrid finite element methods. Springer Series in Computational Mathematics. 15. Springer-Verlag, New York (1991)

  8. Ciarlet, P. G.: The finite element method for elliptic problems, North-Holland Publishing Co., Amsterdam-New York-Oxford. Studies in Mathematics and its Applications, 4 (1978)

  9. Costabel, M., Dauge, M., Singularities of Maxwell’s equations on polyhedral domains. In Analysis, numerics and applications of differential and integral equations (Stuttgart, : vol. 379 of Pitman Res. Notes Math. Ser. Longman, Harlow 1998, 69–76 (1996)

  10. Costabel, M., Dauge, M.: Singularities of electromagnetic fields in polyhedral domains. Arch. Ration. Mech. Anal. 151, 221–276 (2000)

    Article  MathSciNet  Google Scholar 

  11. Costabel, M., Dauge,M.: Weighted regularization of Maxwell equations in polyhedral domains: A rehabilitation of nodal finite elements. Numer. Math. 93: 239–277 (2002)

    Article  MathSciNet  Google Scholar 

  12. Dauge, M., Singularities of corner problems and problems of corner singularities, in Actes du 30ème Congrès d’Analyse Numérique: CANum ’98 (Arles, : vol. 6 of ESAIM Proc., Soc. Math. Appl. Indust. Paris 1999, 19–40 (1998)

  13. Davidson, P. A.: An introduction to magnetohydrodynamics. Cambridge Texts in Applied Mathematics, Cambridge University Press, Cambridge, (2001)

  14. Ding, Q., Long, X., Mao, S.: Convergence analysis of Crank-Nicolson extrapolated fully discrete scheme for thermally coupled incompressible magnetohydrodynamic system. Appl. Numer. Math. 157, 522–543 (2020)

    Article  MathSciNet  Google Scholar 

  15. Dong, X., He, Y.: Optimal convergence analysis of Crank-Nicolson extrapolation scheme for the three-dimensional incompressible magnetohydrodynamics. Comput. Math. Appl. 76, 2678–2700 (2018)

    Article  MathSciNet  Google Scholar 

  16. Gao, H., Qiu, W.: A semi-implicit energy conserving finite element method for the dynamical incompressible magnetohydrodynamics equations. Comput. Methods Appl. Mech. Engrg. 346, 982–1001 (2019)

    Article  MathSciNet  Google Scholar 

  17. Gerbeau, J.-F.: A stabilized finite element method for the incompressible magnetohydrodynamic equations. Numer. Math. 87, 83–111 (2000)

    Article  MathSciNet  Google Scholar 

  18. Gerbeau, J.-F., Le Bris, C., Lelièvre, T.: Mathematical methods for the magnetohydrodynamics of liquid metals. Numerical Mathematics and Scientific Computation, Oxford University Press, Oxford (2006)

  19. Girault, V., Raviart, P.-A.: Finite element methods for Navier-Stokes equations. Springer Series in Computational Mathematics. Theory and algorithms. Springer-Verlag, Berlin (1986)

  20. Greif, C., Li, D., Schötzau, D., Wei, X.: A mixed finite element method with exactly divergence-free velocities for incompressible magnetohydrodynamics. Comput. Methods Appl. Mech. Engrg. 199, 2840–2855 (2010)

    Article  MathSciNet  Google Scholar 

  21. Guermond, J.L., Minev, P.D.: Mixed finite element approximation of an MHD problem involving conducting and insulating regions: the 3D case. Numer. Methods Partial Differ. Equ. 19, 709–731 (2003)

    Article  MathSciNet  Google Scholar 

  22. Gunzburger, M.D., Meir, A.J., Peterson, J.S.: On the existence, uniqueness, and finite element approximation of solutions of the equations of stationary, incompressible magnetohydrodynamics. Math. Comput. 56, 523–563 (1991)

    Article  MathSciNet  Google Scholar 

  23. He, Y.: Unconditional convergence of the Euler semi-implicit scheme for the three-dimensional incompressible MHD equations. IMA J. Numer. Anal. 35, 767–801 (2015)

    Article  MathSciNet  Google Scholar 

  24. Heywood, J.G., Rannacher, R.: Finite element approximation of the nonstationary Navier-Stokes problem: I-regularity of solutions and second-order error estimates for spatial discretization. SIAM J. Numer. Anal. 19, 275–311 (1982)

    Article  MathSciNet  Google Scholar 

  25. Heywood, J.G., Rannacher, R.: Finite-element approximation of the nonstationary Navier-Stokes problem: IV–error analysis for second-order time discretization. SIAM J. Numer. Anal. 27, 353–384 (1990)

    Article  MathSciNet  Google Scholar 

  26. Hiptmair, R.: Finite elements in computational electromagnetism. Acta Numer. 11, 237–339 (2002)

    Article  MathSciNet  Google Scholar 

  27. Hiptmair, R., Li, L., Mao, S., Zheng, W.: A fully divergence-free finite element method for magnetohydrodynamic equations. Math. Models Methods Appl. Sci. 28, 659–695 (2018)

    Article  MathSciNet  Google Scholar 

  28. Hu, K., Ma, Y., Xu, J.: Stable finite element methods preserving \(\nabla \cdot B=0\) exactly for MHD models. Numer. Math. 135, 371–396 (2017)

    Article  MathSciNet  Google Scholar 

  29. Li, B., Wang, J., Xu, L.: A convergent linearized Lagrange finite element method for the magneto-hydrodynamic equations in two-dimensional nonsmooth and nonconvex domains. SIAM J. Numer. Anal. 58, 430–459 (2020)

    Article  MathSciNet  Google Scholar 

  30. Lifschitz, A.E.: Magnetohydrodynamics and spectral theory. Developments in Electromagnetic Theory and Applications. Kluwer Academic Publishers Group, Dordrecht (1989)

  31. Lorca, S.A., Boldrini, J.L.: The initial value problem for a generalized Boussinesq model. Nonlinear Anal. 36, 457–480 (1999)

    Article  MathSciNet  Google Scholar 

  32. Marioni, L., Bay, F., Hachem, E.: Numerical stability analysis and flow simulation of lid-driven cavity subjected to high magnetic field. Phys. Fluids 28, 057102 (2016)

    Article  Google Scholar 

  33. Monk, P.: Finite element methods for Maxwell’s equations. Numerical Mathematics and Scientific Computation. Oxford University Press, New York (2003)

  34. Moreau, R.: Magnetohydrodynamics. vol. 3 of Fluid Mechanics and its Applications, . Translated from the French by A. F. Wright. Kluwer Academic Publishers Group, Dordrecht, (1990)

  35. Nédélec, J.-C.: Mixed finite elements in \({ R}^{3}\). Numer. Math. 35, 315–341 (1980)

    Article  MathSciNet  Google Scholar 

  36. Prohl, A.: Convergent finite element discretizations of the nonstationary incompressible magnetohydrodynamics system, M2AN Math. Model. Numer. Anal. 42, 1065–1087 (2008)

    Article  MathSciNet  Google Scholar 

  37. Schötzau, D.: Mixed finite element methods for stationary incompressible magneto-hydrodynamics. Numer. Math. 96, 771–800 (2004)

    Article  MathSciNet  Google Scholar 

  38. Shi, D., Yu, Z.: Nonconforming mixed finite element methods for stationary incompressible magnetohydrodynamics. Int. J. Numer. Anal. Model. 10, 904–919 (2013)

    MathSciNet  MATH  Google Scholar 

  39. Su, H., Mao, S., Feng, X.: Optimal error estimates of penalty based iterative methods for steady incompressible magnetohydrodynamics equations with different viscosities. J. Sci. Comput. 79, 1078–1110 (2019)

    Article  MathSciNet  Google Scholar 

  40. Tóth, G.: The \(\nabla \cdot B=0\) constraint in shock-capturing magnetohydrodynamics codes. J. Comput. Phys. 161, 605–652 (2000)

    Article  MathSciNet  Google Scholar 

  41. Wiedmer, M.: Finite element approximation for equations of magnetohydrodynamics. Math. Comput. 69, 83–101 (2000)

    Article  MathSciNet  Google Scholar 

  42. Yang, J., He, Y.: Stability and error analysis for the first-order Euler implicit/explicit scheme for the 3D MHD equations. Int. J. Comput. Methods 15, 1750077 (2018)

    Article  MathSciNet  Google Scholar 

  43. Zhang, G.-D., Yang, J., Bi, C.: Second order unconditionally convergent and energy stable linearized scheme for MHD equations. Adv. Comput. Math. 44, 505–540 (2018)

    Article  MathSciNet  Google Scholar 

  44. Zhang, L., Cui, T., Liu, H.: A set of symmetric quadrature rules on triangles and tetrahedra. J. Comput. Math. 27, 89–96 (2009)

    MathSciNet  MATH  Google Scholar 

  45. Zhang, L.-B.: A parallel algorithm for adaptive local refinement of tetrahedral meshes using bisection. Numer. Math. Theory Methods Appl. 2, 65–89 (2009)

    MathSciNet  MATH  Google Scholar 

  46. Zhao, J.: Analysis of finite element approximation for time-dependent Maxwell problems. Math. Comp. 73, 1089–1105 (2004)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors thank the anonymous referees very much for their helpful comments and suggestions which helped to improve the presentation of this paper.

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University, Jinan, 250100, China

    Qianqian Ding

  2. College of Mathematics and Information Science, Henan University of Economics and Law, Zhengzhou, 450047, China

    Xiaonian Long

  3. NCMIS, LSEC, Institute of Computational Mathematics and Scientific/Enginnering Computing, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    Shipeng Mao

  4. School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing, 100049, China

    Qianqian Ding, Xiaonian Long & Shipeng Mao

Authors
  1. Qianqian Ding
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaonian Long
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shipeng Mao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Shipeng Mao.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The first author funded by China Postdoctoral Science Foundation (2021M691951). The third author was supported by National Natural Science Foundation of China (No. 11871467) and the Major State Research Development Program of China (No. 2016YFB0201304).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ding, Q., Long, X. & Mao, S. Error Estimate of a Fully Discrete Finite Element Method for Incompressible Vector Potential Magnetohydrodynamic System. J Sci Comput 88, 71 (2021). https://doi.org/10.1007/s10915-021-01571-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-021-01571-3

Keywords