Fast and Optimal WENO Schemes for Degenerate Parabolic Conservation Laws

Abstract

In this work, we extend the Fast and Optimized Weighted Essentially Non-Oscillatory (FOWENO) schemes for nonlinear degenerate parabolic equations. Fast WENO methods were introduced with the goal of reducing computational costs for the smoothness indicators calculations. Whereas, Optimal WENO schemes were developed to increase the accuracy of the approximation near critical points. Here, both techniques are adapted for degenerate parabolic conservative laws obtaining: FOWENO34 and FOWENO56 reconstructions, where the first and second digit represent the order of approximation for the convective and diffusive flux, respectively. By considering a SSP Runge-Kutta method for the time discretization, an experimental analysis is carried out in order to show the efficiency and accuracy of FOWENO approximations for one and two-dimensional parabolic problems with degenerate diffusion.

WENO34 and WENO56 Reconstructions

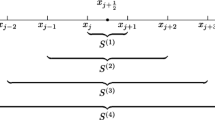
Here, we develop WENO reconstructions for the fluxes ${\hat{f}}_{i+1/2}$, ${\hat{K}}_{i+1/2}$ and for the subfluxes ${\hat{f}}^{m_1}_{i+1/2}$, ${\hat{K}}^{m_2}_{i+1/2}$ defined in (8) associated to the stencils $S_f$ and $S_K$ proposed in (5) for $r=1,2$.

Let us start for the case $r=1$ where the stencils are

$$\begin{aligned} S_f=\{x_{i-1},x_i,x_{i+1}\};\quad S_K=\{x_{i-1},x_i,x_{i+1},x_{i+2}\}, \end{aligned}$$

and the substencils are

$$\begin{aligned} S^{m_1}_f=\{x_{i-1+m_1},x_{i+m_1}\};\quad S^{m_2}_K=\{x_{i-1+m_2},x_{i+m_2}\}, \end{aligned}$$

for $m_1=0,1$ and $m_2=0,1,2.$ Using the values $f(u_{i-1}),f(u_{i}),f(u_{i+1})$, we approximate $f(u_{i+1/2})$ constructing a quadratic polynomial q(x). Obtaining

$$\begin{aligned} {\hat{f}}_{i+1/2}(x_{i-1},x_i,x_{i+1})=q(x_{i+1/2})=-\frac{1}{6}f(u_{i-1})+\frac{5}{6}f(u_{i})+\frac{1}{3}f(u_{i+1}). \end{aligned}$$

Analogously, we calculate polynomials $q^0(x)$ and $q^1(x)$ by considering values $f(u_{i-1}),f(u_{i})$ and $f(u_{i}),f(u_{i+1})$, respectively. Thus,

$$\begin{aligned} {\hat{f}}^0_{i+1/2}(x_{i-1},x_i)=q^0(x_{i+1/2})=-\frac{1}{2}f(u_{i-1})+\frac{3}{2}f(u_{i}) \end{aligned}$$

and

$$\begin{aligned} {\hat{f}}^1_{i+1/2}(x_{i},x_{i+1})=q^1(x_{i+1/2})=\frac{1}{2}f(u_{i})+\frac{1}{2}f(u_{i+1}). \end{aligned}$$

Notice that ${\hat{f}}_{i+1/2}=\frac{1}{3}{\hat{f}}^0_{i+1/2}+\frac{2}{3}{\hat{f}}^1_{i+1/2}$ which is according to Table 1. Now the WENO reconstruction for the convective flux is

$$\begin{aligned} {\hat{f}}_{i+1/2}=\omega _0^f{\hat{f}}^0_{i+1/2}+\omega _1^f{\hat{f}}^1_{i+1/2} \end{aligned}$$

where $\omega _0^f$, $\omega _1^f$ are defined in (9). For the diffusive flux, we get

$$\begin{aligned} {\hat{K}}_{i+1/2}(x_{i-1},x_i,x_{i+1},x_{i+2})=p(x_{i+1/2})= \frac{K_{i-1}-15K_{i}+15K_{i+1}-K_{i+2}}{12}. \end{aligned}$$

In a similar way, using the points $\{K_{i-1+m_2},K_{i+m_2}\}$ with $m_2=0,1,2$, we get the polynomials $p^0(x)$, $p^1(x)$ and $p^2(x)$ satisfying

$$\begin{aligned}&{\hat{K}}^0_{i+1/2}(x_{i-1},x_{i})=p^0(x_{i+1/2})=K_i-K_{i-1},\\&{\hat{K}}^1_{i+1/2}(x_{i},x_{i+1})=p^1(x_{i+1/2})=K_{i+1}-K_{i},\\&{\hat{K}}^2_{i+1/2}(x_{i+1},x_{i+2})=p^2(x_{i+1/2})=K_{i+2}-K_{i+1}. \end{aligned}$$

It is easy to show that $c_0^K=-1/12,c_1^K=7/6,c_2^K=-1/12$. Therefore,

$$\begin{aligned} p(x_{i+1/2})=-\frac{1}{12}p^0(x_{i+1/2})+\frac{7}{6}p^1(x_{i+1/2})-\frac{1}{12}p^2(x_{i+1/2}). \end{aligned}$$

Following the steps described in Section 2.1, we have $\sigma ^+ =\frac{5}{2}$ and $\sigma ^- =\frac{3}{2}$. So, the positive and negative weights are

$$\begin{aligned} \gamma ^+_0=\frac{1}{30},\gamma ^+_1=\frac{14}{15},\gamma ^+_2=\frac{1}{30}, \end{aligned}$$

and

$$\begin{aligned} \gamma ^-_0=\frac{1}{9},\gamma ^-_1=\frac{7}{9},\gamma ^-_2=\frac{1}{9}. \end{aligned}$$

Now we compute the nonlinear weights which are given by

$$\begin{aligned} \omega ^K_{m_2}=\frac{5}{2}\omega ^+_m-\frac{3}{2}\omega ^-_{m_2} \end{aligned}$$

where $\omega ^+_{m_2}$ and $\omega ^-_{m_2}$ are defined in (12). Finally, the reconstruction for the diffusive flux is

$$\begin{aligned} {\hat{K}}_{i+1/2}=\omega _0^K{\hat{K}}^0_{i+1/2}+\omega _1^K{\hat{K}}^1_{i+1/2}+\omega _2^K{\hat{K}}^2_{i+1/2}. \end{aligned}$$

For the case $r=2$, we have

$$\begin{aligned} S_f=\{x_{i-2},x_{i-1},x_{i},x_{i+1},x_{i+2}\};\quad S_K=\{x_{i-2},x_{i-1},x_{i},x_{i+1},x_{i+2},x_{i+3}\}. \end{aligned}$$

Using the same procedure for the case $r=1$, we get

$$\begin{aligned}&{\hat{f}}_{i+1/2}(x_{i-2},x_{i-1},x_{i},x_{i+1},x_{i+2})=q(x_{i+1/2})\\&\quad =\frac{1}{30}f(u_{i-2})-\frac{13}{60}f(u_{i-1})+\frac{47}{60}f(u_{i})+\frac{9}{20}f(u_{i+1})-\frac{1}{20}f(u_{i+2}). \end{aligned}$$

Considering $S^{m_1}_f=\{x_{i-2+m_1},x_{i-1+m_1},x_{i+m_1}\}$ for $m_1=0,1,2$, we compute the fluxes

$$\begin{aligned}&{\hat{f}}^0_{i+1/2}(x_{i-2},x_{i-1},x_{i})=q^0(x_{i+1/2})=\frac{1}{3}f_{i-2}-\frac{7}{6}f_{i-1}+\frac{11}{6}f_{i},\\&{\hat{f}}^{(1)}_{i+1/2}(x_{i-1},x_{i},x_{i+1})=q^1(x_{i+1/2})=-\frac{1}{6}f_{i-1}+\frac{5}{6}f_{i}+\frac{1}{3}f_{i+1},\\&{\hat{f}}^{(2)}_{i+1/2}(x_{i},x_{i+1},x_{i+2})=q^2(x_{i+1/2})=\frac{1}{3}f_{i}+\frac{5}{6}f_{i+1}-\frac{1}{6}f_{i+2}. \end{aligned}$$

and the WENO reconstruction for the convective flux is obtained substituting into equation (7) for ${\hat{f}}_{i+1/2}$ and $\omega _{m_1}^f$ defined in (9). For the diffusive flux, we consider the substencil

$$\begin{aligned} S^{m_2}_K=\{x_{i-2+m_2},x_{i-1+m_2},x_{i+m_2},x_{i+1+m_2}\}, \end{aligned}$$

for $m_2=0,1,2$ and we get

$$\begin{aligned}&{\hat{K}}_{i+1/2}(x_{i-2},x_{i-1},x_{i},x_{i+1},x_{i+2},x_{i+3})=p(x_{i+1/2})\\&\quad =\frac{-2K_{i-3}+25K_{i-2}-245K_{i-1}+245K_{i}-25K_{i+1}+2K_{i+2}}{180} \end{aligned}$$

with

$$\begin{aligned}&{\hat{K}}^0_{i+1/2}(x_{i-2},x_{i-1},x_{i},x_{i+1})=p^0(x_{i+1/2})=\frac{K_{i-2}-3K_{i-1}-9K_{i}+11K_{i+1}}{12},\\&{\hat{K}}^1_{i+1/2}(x_{i-1},x_{i},x_{i+1},x_{i+2})=p ^1(x_{i+1/2})=\frac{K_{i-1}-15K_{i}+15K_{i+1}-K_{i+2}}{12},\\&{\hat{K}}^2_{i+1/2}(x_{i},x_{i+1},x_{i+2},x_{i+3})=p^2(x_{i+1/2})=\frac{-11K_{i}+9K_{i+1}+3K_{i+2}-K_{i+3}}{12}. \end{aligned}$$

The corresponding linear weights satisfy

$$\begin{aligned} {\hat{K}}_{i+1/2}=-\frac{2}{15}{\hat{K}}^0_{i+1/2}+\frac{19}{15}{\hat{K}}^1_{i+1/2}-\frac{2}{15}{\hat{K}}^2_{i+1/2}. \end{aligned}$$

and to calculate the nonlinear weights, we have $\sigma ^+ =\frac{42}{15}$ and $\sigma ^- =\frac{27}{15}$. Thus, the positive and negative weights are

$$\begin{aligned} \gamma ^+_0=\frac{1}{21},\gamma ^+_1=\frac{19}{21},\gamma ^+_2=\frac{1}{21}, \end{aligned}$$

and

$$\begin{aligned} \gamma ^-_0=\frac{4}{27},\gamma ^-_1=\frac{19}{27},\gamma ^-_2=\frac{4}{27}. \end{aligned}$$

Finally the non-linear weights are obtained by

$$\begin{aligned} \omega ^K_m=\frac{42}{15}\omega ^+_m-\frac{27}{15}\omega ^-_m \end{aligned}$$

with $\omega ^+_m$ and $\omega ^-_m$ given in (12), and the WENO reconstruction is written of the form

$$\begin{aligned} {\hat{K}}_{i+1/2}=\omega _0^K{\hat{K}}^0_{i+1/2}+\omega _1^K{\hat{K}}^1_{i+1/2}+\omega _2^K{\hat{K}}^2_{i+1/2}. \end{aligned}$$