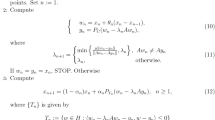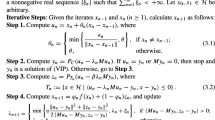Skip to main content
Springer Nature Link
Log in

Subgradient Extragradient Method with Double Inertial Steps for Variational Inequalities

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

In this paper, we obtain successively weak, strong and linear convergence analysis of the sequence of iterates generated by our proposed subgradient extragradient method with double inertial extrapolation steps and self-adaptive step sizes for solving variational inequalities for which the cost operator is pseudo-monotone and Lipschitz continuous in real Hilbert spaces. Our proposed method is a combination of double inertial extrapolation steps, relaxation step and subgradient extragradient method which is aimed to increase the speed of convergence of many available subgradient extragradient methods with inertia for solving variational inequalities. Several versions of subgradient extragradient methods with inertial extrapolation step serve as special cases of our proposed method and the inertia in our proposed method is more relaxed and chosen in [0, 1]. Numerical implementations of our method show that our method is efficient, implementable and the benefits gained when subgradient extragradient method with double inertial extrapolation steps are considered for variational inequalities instead of subgradient extragradient methods with one inertial extrapolation step available in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Aubin, J.-P., Ekeland, I.: Applied Nonlinear Analysis. Wiley, New York (1984)

    MATH  Google Scholar 

  2. Baiocchi, C., Capelo, A.: Variational and Quasivariational Inequalities; Applications to Free Boundary Problems. Wiley, New York (1984)

    MATH  Google Scholar 

  3. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, CMS Books in Mathematics. Springer, New York (2011)

    Book  Google Scholar 

  4. Boţ, R.I., Csetnek, E.R., Vuong, P.T.: The forward-backward-forward method from discrete and continuous perspective for pseudomonotone variational inequalities in Hilbert spaces. Eur. J. Oper. Res. 287(1), 49–60 (2020)

    Article  Google Scholar 

  5. Censor, Y., Gibali, A., Reich, S.: Strong convergence of subgradient extragradient methods for the variational inequality problem in Hilbert space. Optim. Methods Softw. 26, 827–845 (2011)

    Article  MathSciNet  Google Scholar 

  6. Censor, Y., Gibali, A., Reich, S.: The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 148, 318–335 (2011)

    Article  MathSciNet  Google Scholar 

  7. Chang, X., Liu, S., Deng, Z., Li, S.: An inertial subgradient extragradient algorithm with adaptive stepsizes for variational inequality problems. Optim. Methods Softw. (2021). https://doi.org/10.1080/10556788.2021.1910946

    Article  Google Scholar 

  8. Ceng, L.C., Petrusel, A., Qin, X., Yao, J.C.: A modified inertial subgradient extragradient method for solving pseudomonotone variational inequalities and common fixed point problems. Fixed Point Theory 21, 93–108 (2020)

    Article  MathSciNet  Google Scholar 

  9. Ceng, L.C., Petrusel, A., Qin, X., Yao, J.C.: Two inertial subgradient extragradient algorithms for variational inequalities with fixed-point constraints. Optimization 70, 1337–1358 (2021)

    Article  MathSciNet  Google Scholar 

  10. Ceng, L.C., Shang, M.: Hybrid inertial subgradient extragradient methods for variational inequalities and fixed point problems involving asymptotically nonexpansive mappings. Optimization 70, 715–740 (2021)

    Article  MathSciNet  Google Scholar 

  11. Ceng, L.C., Yuan, Q.: Composite inertial subgradient extragradient methods for variational inequalities and fixed point problems. J. Inequal. Appl. Paper No. 274 (2019)

  12. Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer Series in Operations Research, vol. II. Springer, New York (2003)

  13. Fan, J., Liu, L., Qin, X.: A subgradient extragradient algorithm with inertial effects for solving strongly pseudomonotone variational inequalities. Optimization 69, 2199–2215 (2020)

    Article  MathSciNet  Google Scholar 

  14. Glowinski, R., Lions, J.-L., Trémolières, R.: Numerical Analysis of Variational Inequalities. North-Holland, Amsterdam (1981)

    MATH  Google Scholar 

  15. Harker, P.T., Pang, J.-S.: A damped-Newton method for the linear complementarity problem. In: Allgower, G., Georg, K. (eds.) Computational Solution of Nonlinear Systems of Equations, Lectures in Applied Mathematics, vol. 26, pp. 265–284. AMS, Providence (1990)

    Google Scholar 

  16. He, L., Cui, Y.L., Ceng, L.C., Zhao, T.Y., Wang, D.Q., Hu, H.Y.: Strong convergence for monotone bilevel equilibria with constraints of variational inequalities and fixed points using subgradient extragradient implicit rule. J. Inequal. Appl. Paper No. 146 (2021)

  17. Khobotov, E.N.: Modification of the extragradient method for solving variational inequalities and certain optimization problems. USSR Comput. Math. Math. Phys. 27, 120–127 (1989)

    Article  Google Scholar 

  18. Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)

    MATH  Google Scholar 

  19. Konnov, I.V.: Combined Relaxation Methods for Variational Inequalities. Springer-Verlag, Berlin (2001)

    Book  Google Scholar 

  20. Korpelevich, G.M.: The extragradient method for finding saddle points and other problems. Ekonomika i Mat. Metody 12, 747–756 (1976)

    MathSciNet  MATH  Google Scholar 

  21. Maingé, P.-E.: Convergence theorems for inertial KM-type algorithms. J. Comput. Appl. Math. 219, 223–236 (2008)

    Article  MathSciNet  Google Scholar 

  22. Malitsky, Yu.V., Semenov, V.V.: A hybrid method without extrapolation step for solving variational inequality problems. J. Global Optim. 61, 193–202 (2015)

    Article  MathSciNet  Google Scholar 

  23. Marcotte, P.: Applications of Khobotov’s algorithm to variational and network equlibrium problems. Inf. Syst. Oper. Res. 29, 258–270 (1991)

  24. Nagurney, A.: Network Economics: A Variational Inequality Approach. Kluwer Academic Publishers, Dordrecht (1999)

    Book  Google Scholar 

  25. Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 73, 591–597 (1967)

    Article  MathSciNet  Google Scholar 

  26. Shehu, Y., Dong, Q.-L., Jiang, D.: Single projection method for pseudo-monotone variational inequality in Hilbert spaces. Optimization 68, 385–409 (2019)

    Article  MathSciNet  Google Scholar 

  27. Shehu, Y., Iyiola, O.S., Reich, S.: A modified inertial subgradient extragradient method for solving variational inequalities. Optim. Eng. (2021). https://doi.org/10.1007/s11081-020-09593-w

    Article  Google Scholar 

  28. Solodov, M.V., Svaiter, B.F.: A new projection method for variational inequality problems. SIAM J. Control Optim. 37, 765–776 (1999)

    Article  MathSciNet  Google Scholar 

  29. Thong, D.V., Yang, J., Cho, Y.J., Rassias, T.M.: Explicit extragradient-like method with adaptive stepsizes for pseudomonotone variational inequalities. Optim. Lett. 15, 2181–2199 (2021)

    Article  MathSciNet  Google Scholar 

  30. Thong, D.V., Van Hieu, D., Rassias, T.M.: Self adaptive inertial subgradient extragradient algorithms for solving pseudomonotone variational inequality problems. Optim. Lett. 14, 115–144 (2020)

    Article  MathSciNet  Google Scholar 

  31. Thong, D.V., Hieu, D.V.: Inertial extragradient algorithms for strongly pseudomonotone variational inequalities. J. Comput. Appl. Math. 341, 80–98 (2018)

    Article  MathSciNet  Google Scholar 

  32. Tian, M., Tong, M.: Self-adaptive subgradient extragradient method with inertial modification for solving monotone variational inequality problems and quasi-nonexpansive fixed point problems. J. Inequal. Appl. Paper No. 7 (2019)

  33. Vuong, P.T.: On the weak convergence of the extragradient method for solving pseudo-monotone variational inequalities. J. Optim. Theory Appl. 176, 399–409 (2018)

    Article  MathSciNet  Google Scholar 

  34. Yang, J.: Self-adaptive inertial subgradient extragradient algorithm for solving pseudomonotone variational inequalities. Appl. Anal. 100, 1067–1078 (2021)

    Article  MathSciNet  Google Scholar 

  35. Yang, J., Liu, H., Liu, Z.: Modified subgradient extragradient algorithms for solving monotone variational inequalities. Optimization 67, 2247–2258 (2018)

    Article  MathSciNet  Google Scholar 

  36. Yao, J.C.: Variational inequalities with generalized monotone operators. Math. Oper. Res. 19, 691–705 (1994)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Tiangong University, Tianjin, 300387, China

    Yonghong Yao

  2. The Key Laboratory of Intelligent Information and Big Data Processing of NingXia Province, and Health Big Data Research Institute, North Minzu University, Yinchuan, 750021, China

    Yonghong Yao

  3. Department of Mathematics, Clarkson University, Potsdam, NY, USA

    Olaniyi S. Iyiola

  4. College of Mathematics and Computer Science, Zhejiang Normal University, Jinhua, 321004, China

    Yekini Shehu

Authors
  1. Yonghong Yao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Olaniyi S. Iyiola
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yekini Shehu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yekini Shehu.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yao, Y., Iyiola, O.S. & Shehu, Y. Subgradient Extragradient Method with Double Inertial Steps for Variational Inequalities. J Sci Comput 90, 71 (2022). https://doi.org/10.1007/s10915-021-01751-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-021-01751-1

Keywords

Mathematics Subject Classification