Skip to main content
Springer Nature Link
Log in

Unconditionally Energy Stable and Bound-Preserving Schemes for Phase-Field Surfactant Model with Moving Contact Lines

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

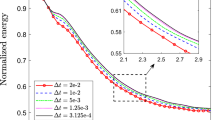
Abstract

Phase-field surfactant model with moving contact lines (PFS-MCL) has been extensively investigated in the study of droplet dynamics on solid surfaces in the presence of surfactants. This model consists of two Cahn–Hilliard type equations, governing the dynamics of interface and surfactant concentration, with the dynamical boundary condition for moving contact lines. Moreover, the total free energy has logarithmic singularity due to Flory–Huggins potential. Based on the convexity of Flory–Huggins potential and the convex splitting technique, we propose a set of unconditionally energy stable and bound-preserving schemes for PFS-MCL model. The proposed schemes are decoupled, uniquely solvable, and mass conservative. These properties are rigorously proved for the first-order fully discrete scheme. In addition, we prove that the second-order fully discrete scheme satisfies all these properties except for the energy stability. We numerically validate the desired properties for both first-order and second-order schemes. We also present numerical results to systematically study the influence of surfactants on contact line dynamics and its parameter dependence. Furthermore, droplet spreading and retracting on chemically patterned surfaces are numerically investigated. It is observed that surfactants can affect contact angle hysteresis by changing advancing/receding contact angles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Anna, S.L., Mayer, H.C.: Microscale tipstreaming in a microfluidic flow focusing device. Phys. Fluids 18(12), 121512 (2006)

    Article  Google Scholar 

  2. Liu, H., Zhang, Y.: Phase-field modeling droplet dynamics with soluble surfactants. J. Comput. Phys. 229(24), 9166–9187 (2010)

    Article  Google Scholar 

  3. Probstein, R.F.: Physicochemical Hydrodynamics: An Introduction. Wiley, New York (2005)

    Google Scholar 

  4. Raffa, P., Broekhuis, A.A., Picchioni, F.: Polymeric surfactants for enhanced oil recovery: a review. J. Petrol. Sci. Eng. 145, 723–733 (2016)

    Article  Google Scholar 

  5. Young, T.: An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 95, 65–87 (1805)

    Google Scholar 

  6. Huh, C., Scriven, L.E.: Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35(1), 85–101 (1971)

    Article  Google Scholar 

  7. de Gennes, P.-G.: Wetting: statics and dynamics. Rev. Mod. Phys. 57(3, part 1), 827–863 (1985). https://doi.org/10.1103/RevModPhys.57.827

    Article  MathSciNet  Google Scholar 

  8. de Gennes, P.-G., Brochard-Wyart, F., Quéré, D., et al.: Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, vol. 315. Springer, New York (2004)

    Book  Google Scholar 

  9. Bonn, D., Eggers, J., Indekeu, J., Meunier, J., Rolley, E.: Wetting and spreading. Rev. Mod. Phys. 81(2), 739 (2009)

    Article  Google Scholar 

  10. Stone, H.A.: A simple derivation of the time-dependent convective–diffusion equation for surfactant transport along a deforming interface. Phys. Fluids A 2(1), 111–112 (1990)

    Article  Google Scholar 

  11. Wong, H., Rumschitzki, D., Maldarelli, C.: On the surfactant mass balance at a deforming fluid interface. Phys. Fluids 8(11), 3203–3204 (1996)

    Article  Google Scholar 

  12. Dunbar, O.R.A., Lam, K.F., Stinner, B.: Phase field modelling of surfactants in multi-phase flow. Interfaces Free Bound. 21(4), 495–547 (2019). https://doi.org/10.4171/ifb/429

    Article  MathSciNet  MATH  Google Scholar 

  13. Garcke, H., Lam, K.F., Stinner, B.: Diffuse interface modelling of soluble surfactants in two-phase flow. Commun. Math. Sci. 12(8), 1475–1522 (2014). https://doi.org/10.4310/CMS.2014.v12.n8.a6

    Article  MathSciNet  MATH  Google Scholar 

  14. Chen, K.-Y., Lai, M.-C.: A conservative scheme for solving coupled surface-bulk convection–diffusion equations with an application to interfacial flows with soluble surfactant. J. Comput. Phys. 257(part A), 1–18 (2014). https://doi.org/10.1016/j.jcp.2013.10.003

    Article  MathSciNet  MATH  Google Scholar 

  15. Dieter-Kissling, K., Marschall, H., Bothe, D.: Direct numerical simulation of droplet formation processes under the influence of soluble surfactant mixtures. Comput. Fluids 113, 93–105 (2015). https://doi.org/10.1016/j.compfluid.2015.01.017

    Article  MathSciNet  MATH  Google Scholar 

  16. Cleret de Langavant, C., Guittet, A., Theillard, M., Temprano-Coleto, F., Gibou, F.: Level-set simulations of soluble surfactant driven flows. J. Comput. Phys. 348, 271–297 (2017). https://doi.org/10.1016/j.jcp.2017.07.003

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu, H., Ba, Y., Wu, L., Li, Z., Xi, G., Zhang, Y.: A hybrid lattice Boltzmann and finite difference method for droplet dynamics with insoluble surfactants. J. Fluid Mech. 837, 381–412 (2018). https://doi.org/10.1017/jfm.2017.859

    Article  MathSciNet  MATH  Google Scholar 

  18. Liu, H., Zhang, J., Ba, Y., Wang, N., Wu, L.: Modelling a surfactant-covered droplet on a solid surface in three-dimensional shear flow. J. Fluid Mech. 897, 33–31 (2020). https://doi.org/10.1017/jfm.2020.416

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhang, Z., Xu, S., Ren, W.: Derivation of a continuum model and the energy law for moving contact lines with insoluble surfactants. Phys. Fluids 26(6), 062103 (2014)

    Article  Google Scholar 

  20. Zhao, Q., Ren, W., Zhang, Z.: A thermodynamically consistent model and its conservative numerical approximation for moving contact lines with soluble surfactants. Comput. Methods Appl. Mech. Engrg. 385, 114033–28 (2021). https://doi.org/10.1016/j.cma.2021.114033

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhu, G., Kou, J., Yao, B., Wu, Y.-S., Yao, J., Sun, S.: Thermodynamically consistent modelling of two-phase flows with moving contact line and soluble surfactants. J. Fluid Mech. 879, 327–359 (2019). https://doi.org/10.1017/jfm.2019.664

    Article  MathSciNet  MATH  Google Scholar 

  22. Xu, J.-J., Ren, W.: A level-set method for two-phase flows with moving contact line and insoluble surfactant. J. Comput. Phys. 263, 71–90 (2014). https://doi.org/10.1016/j.jcp.2014.01.012

    Article  MathSciNet  MATH  Google Scholar 

  23. af Klinteberg, L., Lindbo, D., Tornberg, A.-K.: An explicit Eulerian method for multiphase flow with contact line dynamics and insoluble surfactant. Comput. Fluids 101, 50–63 (2014). https://doi.org/10.1016/j.compfluid.2014.05.029

    Article  MathSciNet  MATH  Google Scholar 

  24. Ganesan, S.: Simulations of impinging droplets with surfactant-dependent dynamic contact angle. J. Comput. Phys. 301, 178–200 (2015). https://doi.org/10.1016/j.jcp.2015.08.026

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhu, G., Kou, J., Yao, J., Li, A., Sun, S.: A phase-field moving contact line model with soluble surfactants. J. Comput. Phys. 405, 109170–29 (2020). https://doi.org/10.1016/j.jcp.2019.109170

    Article  MathSciNet  MATH  Google Scholar 

  26. van der Sman, R.G.M., van der Graaf, S.: Diffuse interface model of surfactant adsorption onto flat and droplet interfaces. Rheol. Acta 46(1), 3–11 (2006)

    Article  Google Scholar 

  27. Engblom, S., Do-Quang, M., Amberg, G., Tornberg, A.-K.: On diffuse interface modeling and simulation of surfactants in two-phase fluid flow. Commun. Comput. Phys. 14(4), 879–915 (2013). https://doi.org/10.4208/cicp.120712.281212a

    Article  MathSciNet  MATH  Google Scholar 

  28. Yun, A., Li, Y., Kim, J.: A new phase-field model for a water–oil-surfactant system. Appl. Math. Comput. 229, 422–432 (2014). https://doi.org/10.1016/j.amc.2013.12.054

    Article  MathSciNet  MATH  Google Scholar 

  29. Zhu, G., Kou, J., Sun, S., Yao, J., Li, A.: Numerical approximation of a phase-field surfactant model with fluid flow. J. Sci. Comput. 80(1), 223–247 (2019). https://doi.org/10.1007/s10915-019-00934-1

    Article  MathSciNet  MATH  Google Scholar 

  30. Soligo, G., Roccon, A., Soldati, A.: Coalescence of surfactant-laden drops by phase field method. J. Comput. Phys. 376, 1292–1311 (2019). https://doi.org/10.1016/j.jcp.2018.10.021

    Article  MathSciNet  MATH  Google Scholar 

  31. Eyre, D.J.: Unconditionally gradient stable time marching the Cahn–Hilliard equation. In: Computational and Mathematical Models of Microstructural Evolution (San Francisco, CA, 1998). Materials Research Society Symposium Proceedings, vol. 529, pp. 39–46. MRS, Warrendale, PA, San Francisco (1998). https://doi.org/10.1557/PROC-529-39

  32. Gu, S., Zhang, H., Zhang, Z.: An energy-stable finite-difference scheme for the binary fluid–surfactant system. J. Comput. Phys. 270, 416–431 (2014). https://doi.org/10.1016/j.jcp.2014.03.060

    Article  MathSciNet  MATH  Google Scholar 

  33. Chen, L.Q., Shen, J.: Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 108(2–3), 147–158 (1998)

    Article  Google Scholar 

  34. Xu, C., Tang, T.: Stability analysis of large time-stepping methods for epitaxial growth models. SIAM J. Numer. Anal. 44(4), 1759–1779 (2006). https://doi.org/10.1137/050628143

    Article  MathSciNet  MATH  Google Scholar 

  35. Yang, X.: Error analysis of stabilized semi-implicit method of Allen–Cahn equation. Discrete Contin. Dyn. Syst. Ser. B 11(4), 1057–1070 (2009). https://doi.org/10.3934/dcdsb.2009.11.1057

    Article  MathSciNet  MATH  Google Scholar 

  36. Badia, S., Guillén-González, F., Gutiérrez-Santacreu, J.V.: Finite element approximation of nematic liquid crystal flows using a saddle-point structure. J. Comput. Phys. 230(4), 1686–1706 (2011). https://doi.org/10.1016/j.jcp.2010.11.033

    Article  MathSciNet  MATH  Google Scholar 

  37. Yang, X.: Linear, first and second-order, unconditionally energy stable numerical schemes for the phase field model of homopolymer blends. J. Comput. Phys. 327, 294–316 (2016). https://doi.org/10.1016/j.jcp.2016.09.029

    Article  MathSciNet  MATH  Google Scholar 

  38. Zhao, J., Wang, Q., Yang, X.: Numerical approximations for a phase field dendritic crystal growth model based on the invariant energy quadratization approach. Int. J. Numer. Methods Eng. 110(3), 279–300 (2017). https://doi.org/10.1002/nme.5372

    Article  MathSciNet  MATH  Google Scholar 

  39. Han, D., Brylev, A., Yang, X., Tan, Z.: Numerical analysis of second order, fully discrete energy stable schemes for phase field models of two-phase incompressible flows. J. Sci. Comput. 70(3), 965–989 (2017). https://doi.org/10.1007/s10915-016-0279-5

    Article  MathSciNet  MATH  Google Scholar 

  40. Chen, C., Pan, K., Yang, X.: Numerical approximations of a hydro-dynamically coupled phase-field model for binary mixture of passive/active nematic liquid crystals and viscous fluids. Appl. Numer. Math. 158, 1–21 (2020). https://doi.org/10.1016/j.apnum.2020.07.014

    Article  MathSciNet  MATH  Google Scholar 

  41. Yang, X., Ju, L.: Linear and unconditionally energy stable schemes for the binary fluid–surfactant phase field model. Comput. Methods Appl. Mech. Eng. 318, 1005–1029 (2017). https://doi.org/10.1016/j.cma.2017.02.011

    Article  MathSciNet  MATH  Google Scholar 

  42. Xu, C., Chen, C., Yang, X., He, X.: Numerical approximations for the hydrodynamics coupled binary surfactant phase field model: second-order, linear, unconditionally energy stable schemes. Commun. Math. Sci. 17(3), 835–858 (2019). https://doi.org/10.4310/CMS.2019.v17.n3.a10

    Article  MathSciNet  MATH  Google Scholar 

  43. Yang, X., Yu, H.: Efficient second order unconditionally stable schemes for a phase field moving contact line model using an invariant energy quadratization approach. SIAM J. Sci. Comput. 40(3), 889–914 (2018). https://doi.org/10.1137/17M1125005

    Article  MathSciNet  MATH  Google Scholar 

  44. Shen, J., Xu, J., Yang, J.: The scalar auxiliary variable (SAV) approach for gradient flows. J. Comput. Phys. 353, 407–416 (2018). https://doi.org/10.1016/j.jcp.2017.10.021

    Article  MathSciNet  MATH  Google Scholar 

  45. Shen, J., Xu, J., Yang, J.: A new class of efficient and robust energy stable schemes for gradient flows. SIAM Rev. 61(3), 474–506 (2019). https://doi.org/10.1137/17M1150153

    Article  MathSciNet  MATH  Google Scholar 

  46. Shen, J., Xu, J.: Convergence and error analysis for the scalar auxiliary variable (SAV) schemes to gradient flows. SIAM J. Numer. Anal. 56(5), 2895–2912 (2018). https://doi.org/10.1137/17M1159968

    Article  MathSciNet  MATH  Google Scholar 

  47. Qin, Y., Xu, Z., Zhang, H., Zhang, Z.: Fully decoupled, linear and unconditionally energy stable schemes for the binary fluid–surfactant model. Commun. Comput. Phys. 28(4), 1389–1414 (2020). https://doi.org/10.4208/cicp.oa-2019-0175

    Article  MathSciNet  MATH  Google Scholar 

  48. Yang, J., Kim, J.: An improved scalar auxiliary variable (SAV) approach for the phase-field surfactant model. Appl. Math. Model. 90, 11–29 (2021). https://doi.org/10.1016/j.apm.2020.08.045

    Article  MathSciNet  MATH  Google Scholar 

  49. Cheng, Q., Liu, C., Shen, J.: A new Lagrange multiplier approach for gradient flows. Comput. Methods Appl. Mech. Eng. 367, 113070–20 (2020). https://doi.org/10.1016/j.cma.2020.113070

    Article  MathSciNet  MATH  Google Scholar 

  50. Huang, F., Shen, J., Yang, Z.: A highly efficient and accurate new scalar auxiliary variable approach for gradient flows. SIAM J. Sci. Comput. 42(4), 2514–2536 (2020). https://doi.org/10.1137/19M1298627

    Article  MathSciNet  MATH  Google Scholar 

  51. Yang, X.: A novel fully-decoupled, second-order and energy stable numerical scheme of the conserved Allen–Cahn type flow-coupled binary surfactant model. Comput. Methods Appl. Mech. Engrg. 373, 113502–26 (2021). https://doi.org/10.1016/j.cma.2020.113502

    Article  MathSciNet  MATH  Google Scholar 

  52. Hong, Q., Li, J., Wang, Q.: Supplementary variable method for structure-preserving approximations to partial differential equations with deduced equations. Appl. Math. Lett. 110, 106576–9 (2020). https://doi.org/10.1016/j.aml.2020.106576

    Article  MathSciNet  MATH  Google Scholar 

  53. Du, Q., Nicolaides, R.A.: Numerical analysis of a continuum model of phase transition. SIAM J. Numer. Anal. 28(5), 1310–1322 (1991). https://doi.org/10.1137/0728069

    Article  MathSciNet  MATH  Google Scholar 

  54. Du, Q., Ju, L., Li, X., Qiao, Z.: Maximum bound principles for a class of semilinear parabolic equations and exponential time-differencing schemes. SIAM Rev. 63(2), 317–359 (2021). https://doi.org/10.1137/19M1243750

    Article  MathSciNet  MATH  Google Scholar 

  55. Gao, M., Wang, X.-P.: A gradient stable scheme for a phase field model for the moving contact line problem. J. Comput. Phys. 231(4), 1372–1386 (2012). https://doi.org/10.1016/j.jcp.2011.10.015

    Article  MathSciNet  MATH  Google Scholar 

  56. Shen, J., Yang, X., Yu, H.: Efficient energy stable numerical schemes for a phase field moving contact line model. J. Comput. Phys. 284, 617–630 (2015). https://doi.org/10.1016/j.jcp.2014.12.046

    Article  MathSciNet  MATH  Google Scholar 

  57. Kang, F., Zhang, Z.: A multiple scalar auxiliary variables approach to the energy stable scheme of the moving contact line problem. Numer. Math. Theory Methods Appl. 13(2), 539–568 (2020). https://doi.org/10.4208/nmtma

    Article  MathSciNet  MATH  Google Scholar 

  58. Zhu, G., Kou, J., Sun, S., Yao, J., Li, A.: Decoupled, energy stable schemes for a phase-field surfactant model. Comput. Phys. Commun. 233, 67–77 (2018). https://doi.org/10.1016/j.cpc.2018.07.003

    Article  MathSciNet  Google Scholar 

  59. Chen, W., Wang, C., Wang, X., Wise, S.M.: Positivity-preserving, energy stable numerical schemes for the Cahn–Hilliard equation with logarithmic potential. J. Comput. Phys. X 3, 100031–29 (2019). https://doi.org/10.1016/j.jcpx.2019.100031

    Article  MathSciNet  Google Scholar 

  60. Dong, L., Wang, C., Wise, S.M., Zhang, Z.: A positivity-preserving, energy stable scheme for a ternary Cahn–Hilliard system with the singular interfacial parameters. J. Comput. Phys. 442, 110451–29 (2021). https://doi.org/10.1016/j.jcp.2021.110451

    Article  MathSciNet  MATH  Google Scholar 

  61. Yuan, M., Chen, W., Wang, C., Wise, S.M., Zhang, Z.: An energy stable finite element scheme for the three-component Cahn–Hilliard-type model for macromolecular microsphere composite hydrogels. J. Sci. Comput. 87(3), 1–30 (2021). https://doi.org/10.1007/s10915-021-01508-w

    Article  MathSciNet  MATH  Google Scholar 

  62. Liu, C., Wang, C., Wise, S.M., Yue, X., Zhou, S.: A positivity-preserving, energy stable and convergent numerical scheme for the Poisson–Nernst–Planck system. Math. Comp. 90(331), 2071–2106 (2021). https://doi.org/10.1090/mcom/3642

    Article  MathSciNet  MATH  Google Scholar 

  63. Shen, J., Xu, J.: Unconditionally positivity preserving and energy dissipative schemes for Poisson–Nernst–Planck equations. Numer. Math. 148(3), 671–697 (2021). https://doi.org/10.1007/s00211-021-01203-w

    Article  MathSciNet  MATH  Google Scholar 

  64. He, D., Pan, K., Yue, X.: A positivity preserving and free energy dissipative difference scheme for the Poisson–Nernst–Planck system. J. Sci. Comput. 81(1), 436–458 (2019). https://doi.org/10.1007/s10915-019-01025-x

    Article  MathSciNet  MATH  Google Scholar 

  65. Jin, S., Wang, L.: An asymptotic preserving scheme for the Vlasov–Poisson–Fokker–Planck system in the high field regime. Acta Math. Sci. Ser. B (Engl. Ed.) 31(6, [November 2010 on cover]), 2219–2232 (2011). https://doi.org/10.1016/S0252-9602(11)60395-0

  66. Liu, J.-G., Wang, L., Zhou, Z.: Positivity-preserving and asymptotic preserving method for 2D Keller–Segal equations. Math. Comput. 87(311), 1165–1189 (2018). https://doi.org/10.1090/mcom/3250

    Article  MathSciNet  MATH  Google Scholar 

  67. Li, B., Yang, J., Zhou, Z.: Arbitrarily high-order exponential cut-off methods for preserving maximum principle of parabolic equations. SIAM J. Sci. Comput. 42(6), 3957–3978 (2020). https://doi.org/10.1137/20M1333456

    Article  MathSciNet  MATH  Google Scholar 

  68. Gu, Y., Shen, J.: Bound preserving and energy dissipative schemes for porous medium equation. J. Comput. Phys. 410, 109378–21 (2020). https://doi.org/10.1016/j.jcp.2020.109378

    Article  MathSciNet  MATH  Google Scholar 

  69. van der Vegt, J.J.W., Xia, Y., Xu, Y.: Positivity preserving limiters for time-implicit higher order accurate discontinuous Galerkin discretizations. SIAM J. Sci. Comput. 41(3), 2037–2063 (2019). https://doi.org/10.1137/18M1227998

    Article  MathSciNet  MATH  Google Scholar 

  70. Huang, F., Shen, J.: Bound/positivity preserving and energy stable scalar auxiliary variable schemes for dissipative systems: applications to Keller-Segel and Poisson-Nernst-Planck equations. SIAM J. Sci. Comput. 43(3), 1832–1857 (2021). https://doi.org/10.1137/20M1365417

    Article  MathSciNet  MATH  Google Scholar 

  71. Villani, C.: Topics in Optimal Transportation. Graduate Studies in Mathematics, vol. 58, p. 370. American Mathematical Society, Providence (2003). https://doi.org/10.1090/gsm/058

  72. Li, W., Ying, L.: Hessian transport gradient flows. Res. Math. Sci. 6(4), 34–20 (2019). https://doi.org/10.1007/s40687-019-0198-9

    Article  MathSciNet  MATH  Google Scholar 

  73. Qian, T., Wang, X.-P., Sheng, P.: Molecular scale contact line hydrodynamics of immiscible flows. Phys. Rev. E 68(1), 016306 (2003)

    Article  Google Scholar 

  74. Xu, X., Di, Y., Yu, H.: Sharp-interface limits of a phase-field model with a generalized Navier slip boundary condition for moving contact lines. J. Fluid Mech. 849, 805–833 (2018). https://doi.org/10.1017/jfm.2018.428

    Article  MathSciNet  MATH  Google Scholar 

  75. Nauman, E.B., He, D.Q.: Nonlinear diffusion and phase separation. Chem. Eng. Sci. 56(6), 1999–2018 (2001)

    Article  Google Scholar 

  76. Wang, S., Zhou, S., Shi, S., Chen, W.: Fully decoupled and energy stable BDF schemes for a class of Keller–Segel equations. J. Comput. Phys. 449, 110799 (2022). https://doi.org/10.1016/j.jcp.2021.110799

    Article  MathSciNet  MATH  Google Scholar 

  77. Brandon, S., Marmur, A.: Simulation of contact angle hysteresis on chemically heterogeneous surfaces. J. Colloid Interface Sci. 183(2), 351–355 (1996)

    Article  Google Scholar 

  78. Wang, X.-P., Qian, T., Sheng, P.: Moving contact line on chemically patterned surfaces. J. Fluid Mech. 605, 59–78 (2008). https://doi.org/10.1017/S0022112008001456

    Article  MathSciNet  MATH  Google Scholar 

  79. Zhong, H., Wang, X.-P., Sun, S.: A numerical study of three-dimensional droplets spreading on chemically patterned surfaces. Discrete Contin. Dyn. Syst. Ser. B 21(8), 2905–2926 (2016). https://doi.org/10.3934/dcdsb.2016079

    Article  MathSciNet  MATH  Google Scholar 

  80. Chai, S., Zhang, Z., Zhang, Z.: A second order accuracy preserving method for moving contact lines with stokes flow. J. Comput. Phys. 445, 110607 (2021)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge many helpful discussions with Jie Shen and Jie Xu during the preparation of the paper. The authors would also like to dedicate this paper to Hui Zhang for his departure. The work of Zhen Zhang was partially supported by the NSFC Grant (No. 11731006) and (No. 12071207), NSFC Tianyuan-Pazhou grant (No. 12126602), the Guangdong Basic and Applied Basic Research Foundation (2021A1515010359) and the Guangdong Provincial Key Laboratory of Computational Science and Material Design (No. 2019B030301001).

Author information

Authors and Affiliations

  1. Department of Mathematics, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China

    Chenxi Wang

  2. Department of Mathematics, Southern University of Science and Technology (SUSTech), Shenzhen, 518055, People’s Republic of China

    Chenxi Wang & Zhen Zhang

  3. Department of Mathematics, Virginia Polytechnic Institute and State University, Blacksburg, VA, 24060, USA

    Yichen Guo

  4. Guangdong Provincial Key Laboratory of Computational Science and Material Design, International Center for Mathematics, National Center for Applied Mathematics (Shenzhen), Southern University of Science and Technology (SUSTech), Shenzhen, 518055, People’s Republic of China

    Zhen Zhang

Authors
  1. Chenxi Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yichen Guo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhen Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhen Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, C., Guo, Y. & Zhang, Z. Unconditionally Energy Stable and Bound-Preserving Schemes for Phase-Field Surfactant Model with Moving Contact Lines. J Sci Comput 92, 20 (2022). https://doi.org/10.1007/s10915-022-01863-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-01863-2

Keywords