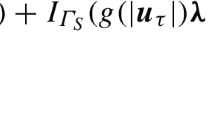Skip to main content
SpringerLink
Log in

A Pressure Projection Stabilized Mixed Finite Element Method for a Stokes Hemivariational Inequality

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

This paper is devoted to the development and analysis of a pressure projection stabilized mixed finite element method, with continuous piecewise linear approximations of velocities and pressures, for solving a hemivariational inequality of the stationary Stokes equations with a nonlinear non-monotone slip boundary condition. We present an existence result for an abstract mixed hemivariational inequality and apply it for a unique solvability analysis of the numerical method for the Stokes hemivariational inequality. An optimal order error estimate is derived for the numerical solution under appropriate solution regularity assumptions. Numerical results are presented to illustrate the theoretical prediction of the convergence order.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data Availability

Not applicable.

References

  1. Atkinson, K., Han, W.: Theoretical Numerical Analysis: A Functional Analysis Framework, 3rd edn. Springer, New York (2009)

    MATH  Google Scholar 

  2. Barboteu, M., Bartosz, K., Han, W., Janiczko, T.: Numerical analysis of a hyperbolic hemivariational inequality arising in dynamic contact. SIAM J. Numer. Anal. 53, 527–550 (2015)

    Article  MathSciNet  Google Scholar 

  3. Barboteu, M., Bartosz, K., Kalita, P.: An analytical and numerical approach to a bilateral contact problem with nonmonotone friction. Int. J. Appl. Math. Comput. Sci. 23, 263–276 (2013)

    Article  MathSciNet  Google Scholar 

  4. Barth, T., Bochev, P.B., Gunzburger, M., Shadid, J.: A taxonomy of consistently stabilized finite element methods for the Stokes problem. SIAM J. Sci. Comput. 25, 1585–1607 (2004)

    Article  MathSciNet  Google Scholar 

  5. Becker, R., Braack, M.: A finite elements pressure gradient stabilization for the Stokes equations based on local projections. Calcolo 38, 173–199 (2000)

    Article  MathSciNet  Google Scholar 

  6. Blasco, J., Codina, R.: Stabilization finite elements method for the transient Navier-Stokes equations based on a pressure gradient projection. Comput. Methods Appl. Mech. Engrg. 182, 277–300 (2000)

    Article  MathSciNet  Google Scholar 

  7. Bochev, P.B., Dohrmann, C.R., Gunzburger, M.D.: Stabilization of low-order mixed finite elements for the Stokes equations. SIAM J. Numer. Anal. 44, 82–101 (2006)

    Article  MathSciNet  Google Scholar 

  8. Bochev, P.B., Gunzburger, M.D.: An absolutely stable pressure-Poisson stabilized finite element method for the Stokes equations. SIAM J. Numer. Anal. 42, 1189–1207 (2004)

    Article  MathSciNet  Google Scholar 

  9. Brenner, S.C., Scott, R.L.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, Vol. 15, Springer-Verlag (2008)

  10. Carl, S., Le, V.K., Motreanu, D.: Nonsmooth Variational Problems and Their Inequalities: Comparison Principles and Applications. Springer, New York (2007)

    Book  Google Scholar 

  11. Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North Holland, Amsterdam (1978)

    MATH  Google Scholar 

  12. Clarke, F.H.: Optimization and Nonsmooth Analysis. Wiley, Interscience, New York (1983)

    MATH  Google Scholar 

  13. Fang, C., Czuprynski, K., Han, W., Cheng, X.L., Dai, X.: Finite element method for a stationary Stokes hemivariational inequality with slip boundary condition. IMA J. Numer. Anal. 40, 2696–2716 (2020)

    Article  MathSciNet  Google Scholar 

  14. Feng, F., Han, W., Huang, J.: Virtual element method for an elliptic hemivariational inequality with applications to contact mechanics. J. Sci. Comput. 81, 2388–2412 (2019)

    Article  MathSciNet  Google Scholar 

  15. Granas, A., Dugundji, J.: Fixed Point Theory. Springer-Verlag, New York Inc (2003)

    Book  Google Scholar 

  16. Han, W.: Numerical analysis of stationary variational-hemivariational inequalities with applications in contact mechanics. Math. Mech. Solids 23, 279–293 (2018)

    Article  MathSciNet  Google Scholar 

  17. Han, W., Czuprynski, K., Jing, F.: Mixed finite element method for a hemivariational inequality of stationary Navier-Stokes equations. J. Sci. Comput. 89, (2021), article number 8

  18. Han, W., Migórski, S., Sofonea, M.: A class of variational-hemivariational inequalities with applications to frictional contact problems. SIAM J. Math. Anal. 46, 3891–3912 (2014)

    Article  MathSciNet  Google Scholar 

  19. Han, W., Sofonea, M.: Numerical analysis of hemivariational inequalities in contact mechanics. Acta Numer. 28, 175–286 (2019)

    Article  MathSciNet  Google Scholar 

  20. Han, W., Sofonea, M., Barboteu, M.: Numerical analysis of elliptic hemivariational inequalities. SIAM J. Numer. Anal. 55, 640–663 (2017)

    Article  MathSciNet  Google Scholar 

  21. Han, W., Sofonea, M., Danan, D.: Numerical analysis of stationary variational-hemivariational inequalities. Numer. Math. 139, 563–592 (2018)

    Article  MathSciNet  Google Scholar 

  22. Han, W., Wang, C.: Numerical analysis of a parabolic hemivariational inequality for semipermeable media. J. Comput. Appl. Math. 389, (2021), article number 113326

  23. Haslinger, J., Miettinen, M., Panagiotopoulos, P.D.: Finite Element Method for Hemivariational Inequalities: Theory, Methods and Applications. Kluwer Academic, Dordrecht (1999)

    Book  Google Scholar 

  24. He, Y., Wang, A., Mei, L.: Stabilized finite element method for the stationary Navier-Stokes equations. J. Eng. Math. 51, 367–380 (2005)

    Article  MathSciNet  Google Scholar 

  25. Jing, F., Han, W., Zhang, Y., Yan, W.: Analysis of an a posteriori error estimator for a variational inequality governed by the Stokes equations. J. Comput. Appl. Math. 372, (2020), article number 112721

  26. Li, J., Jing, F., Chen, Z., Liu, X.: A priori and a posteriori estimates of stabilized mixed finite volume methods for the incompressible flow arising in arteriosclerosis. J. Comput. Appl. Math. 363, 35–52 (2020)

    Article  MathSciNet  Google Scholar 

  27. Li, Y., Li, K.: Pressure projection stabilized finite element method for Navier-Stokes equations with nonlinear slip boundary conditions. Computing 87, 113–133 (2010)

    Article  MathSciNet  Google Scholar 

  28. Li, Y., Li, K.: Pressure projection stabilized finite element method for Stokes problem with nonlinear slip boundary conditions. J. Comput. Appl. Math. 235, 3673–3682 (2011)

    Article  MathSciNet  Google Scholar 

  29. Ling, M., Wang, F., Han, W.: The nonconforming virtual element method for a stationary Stokes hemivariational inequality with slip boundary condition. J. Sci. Comput. 85, (2020), article number 56

  30. Migórski, S., Ochal, A., Sofonea, M.: Nonlinear Inclusions and Hemivariational Inequalities: Models and Analysis of Contact Problems. Springer-Verlag, New York (2013)

    Book  Google Scholar 

  31. Naniewicz, Z., Panagiotopoulos, P.D.: Mathematical Theory of Hemivariational Inequalities and Applications. Marcel Dekker, New York (1995)

    MATH  Google Scholar 

  32. Nečas, J., Hlaváček, I.: Mathematical Theory of Elastic and Elastico-Plastic Bodies: An Introduction. Elsevier Scientific Publishing Company, Amsterdam, Oxford, New York (1981)

    MATH  Google Scholar 

  33. Panagiotopoulos, P.D.: Hemivariational Inequalities, Applications in Mechanics and Engineering. Springer-Verlag, Berlin (1993)

    Book  Google Scholar 

  34. Scott, R.L., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comput. 54, 483–493 (1990)

    Article  MathSciNet  Google Scholar 

  35. Silvester, D.J.: Optimal low order finite element methods for incompressible flow. Comput. Methods Appl. Mech. Engrg. 111, 357–368 (1994)

    Article  MathSciNet  Google Scholar 

  36. Sofonea, M., Migórski, S.: Variational-Hemivariational Inequalities with Applications. Chapman & Hall/CRC Press, Boca Raton-London (2018)

    MATH  Google Scholar 

  37. Temam, R.: Navier-Stokes Equations: Theory and Numerical Analysis. North-Holland, Amsterdam (1979)

    MATH  Google Scholar 

  38. Wang, F., Qi, H.: A discontinuous Galerkin method for an elliptic hemivariational inequality for semipermeable media. Appl. Math. Lett. 109, (2020), article number 106572

  39. Wang, F., Wu, B., Han, W.: The virtual element method for general elliptic hemivariational inequalities. J. Comput. Appl. Math. 389, (2021), article number 113330

  40. Xu, W., Huang, Z., Han, W., Chen, W., Wang, C.: Numerical analysis of history-dependent hemivariational inequalities and applications to viscoelastic contact problems with normal penetration. Comput. Math. Appl. 77, 2596–2607 (2019)

    Article  MathSciNet  Google Scholar 

Download references

Funding

The work of second author was supported by Simons Foundation Collaboration, USA, Grants No. 850737, and by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie Grant Agreement No. 823731 CONMECH. The work of third author was supported by NNSF of China Grant No. 12001478, and the Natural Science Foundation of Guangxi Grant Nos. 2021GXNSFFA196004 and 2020GXNSFBA297137.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, Shaanxi, 710049, China

    Min Ling

  2. Department of Mathematics, University of Iowa, Iowa City, IA, 52242, USA

    Weimin Han

  3. Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Big Data Processing, Yulin Normal University, Yulin, 537000, China

    Shengda Zeng

Authors
  1. Min Ling
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weimin Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shengda Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Min Ling.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ling, M., Han, W. & Zeng, S. A Pressure Projection Stabilized Mixed Finite Element Method for a Stokes Hemivariational Inequality. J Sci Comput 92, 13 (2022). https://doi.org/10.1007/s10915-022-01871-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-01871-2

Keywords

Search

Navigation