Skip to main content
Springer Nature Link
Log in

Flux Globalization Based Well-Balanced Path-Conservative Central-Upwind Schemes for Shallow Water Models

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

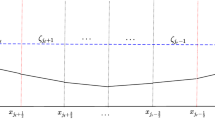
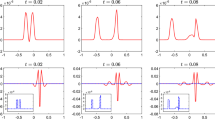
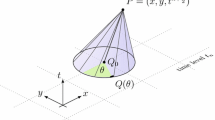
We extend recently proposed flux globalization based well-balanced path-conservative central-upwind schemes to several shallow water models including the Saint-Vevant system with and without the Manning friction term and rotating shallow water equations. We focus on development of the well-balanced schemes capable of exactly preserving quite complicated steady-state solutions the studied systems admit when the bottom topography is discontinuous. In such cases, nonconservative product terms naturally appear and they require a special treatment. To this end, we incorporate the nonconservative product terms into the global fluxes using the path-conservative technique implemented within a framework of simple—yet highly accurate and robust—Riemann-problem-solver-free central-upwind schemes. This results in new flux globalization based central-upwind schemes, which are more accurate than their existing counterparts. The advantages of the proposed schemes are demonstrated on a number of numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data and Software Availability

The data that support the findings of this study and FORTRAN codes developed by the authors and used to obtain all of the presented numerical results are available from the corresponding author upon reasonable request.

References

  1. Bermúdez, A., Vázquez-Cendón, M.E.: Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 23, 1049–1071 (1994)

    Article  MathSciNet  Google Scholar 

  2. Bouchut, F.: Nonlinear stability of finite volume methods for hyperbolic conservation laws and well-balanced schemes for sources, Frontiers in Mathematics, Birkhäuser Verlag, Basel (2004)

  3. Busto, S., Dumbser, M., Gavrilyuk, S., Ivanova, K.: On thermodynamically compatible finite volume methods and path-conservative ADER discontinuous Galerkin schemes for turbulent shallow water flows. J. Sci. Comput., 88 (2021). Paper No. 28, 45 pp

  4. Caselles, V., Donat, R., Haro, G.: Flux-gradient and source-term balancing for certain high resolution shock-capturing schemes. Comput. & Fluids 38, 16–36 (2009)

    Article  MathSciNet  Google Scholar 

  5. Castro, M.J., Morales de Luna, T., Parés, C.: Well-balanced schemes and path-conservative numerical methods. In: Handbook of numerical methods for hyperbolic problems, vol. 18 of Handb. Numer. Anal., Elsevier/North-Holland, Amsterdam, pp. 131–175 (2017)

  6. Castro, M.J., Parés, C.: Well-balanced high-order finite volume methods for systems of balance laws. J. Sci. Comput., 82 (2020). Paper No. 48, 48 pp

  7. Castro Díaz, M.J., Kurganov, A., Morales de Luna, T.: Path-conservative central-upwind schemes for nonconservative hyperbolic systems. ESAIM Math. Model. Numer. Anal. 53, 959–985 (2019)

    Article  MathSciNet  Google Scholar 

  8. Casulli, V.: Semi-implicit finite difference methods for the two-dimensional shallow water equations. J. Comput. Phys. 86, 56–74 (1990)

    Article  MathSciNet  Google Scholar 

  9. Casulli, V., Walters, R.A.: An unstructured grid, three-dimensional model based on the shallow water equations. Int. J. Numer. Methods Fluids 32, 331–348 (2000)

    Article  Google Scholar 

  10. Cheng, Y., Chertock, A., Herty, M., Kurganov, A., Wu, T.: A new approach for designing moving-water equilibria preserving schemes for the shallow water equations. J. Sci. Comput. 80, 538–554 (2019)

    Article  MathSciNet  Google Scholar 

  11. Cheng, Y., Kurganov, A.: Moving-water equilibria preserving central-upwind schemes for the shallow water equations. Commun. Math. Sci. 14, 1643–1663 (2016)

    Article  MathSciNet  Google Scholar 

  12. Chertock, A., Cui, S., Kurganov, A., Özcan, ŞN., Tadmor, E.: Well-balanced schemes for the Euler equations with gravitation: Conservative formulation using global fluxes. J. Comput. Phys. 358, 36–52 (2018)

    Article  MathSciNet  Google Scholar 

  13. Chertock, A., Cui, S., Kurganov, A., Wu, T.: Well-balanced positivity preserving central-upwind scheme for the shallow water system with friction terms. Int. J. Numer. Methods Fluids 78, 355–383 (2015)

    Article  MathSciNet  Google Scholar 

  14. Chertock, A., Dudzinski, M., Kurganov, A., Lukáčová-Medviďová, M.: Well-balanced schemes for the shallow water equations with Coriolis forces. Numer. Math. 138, 939–973 (2018)

    Article  MathSciNet  Google Scholar 

  15. Chertock, A., Herty, M., Özcan, Ş.N.: Well-balanced central-upwind schemes for \(2\,\times \,2\) systems of balance laws, in Theory, Numerics and Applications of Hyperbolic Problems I, vol. 236 of Springer Proceedings in Mathematics & Statistics, Springer, pp. 345–361 (2018)

  16. Chertock, A., Kurganov, A., Liu, X., Liu, Y., Wu, T.: Well-balancing via flux globalization: Applications to shallow water equations with wet/dry fronts. J. Sci. Comput., 90 (2022). Published online on November 20, 2021

  17. Chertock, A., Kurganov, A., Liu, Y.: Central-upwind schemes for the system of shallow water equations with horizontal temperature gradients. Numer. Math. 127, 595–639 (2014)

    Article  MathSciNet  Google Scholar 

  18. Dal Maso, G., Lefloch, P.G., Murat, F.: Definition and weak stability of nonconservative products. J. Math. Pures Appl. 74, 483–548 (1995)

    MathSciNet  MATH  Google Scholar 

  19. Desveaux, V., Masset, A.: A fully well-balanced scheme for shallow water equations with Coriolis force, arXiv preprint arXiv:2105.08357, (2021)

  20. Donat, D., Martinez-Gavara, A.: Hybrid second order schemes for scalar balance laws. J. Sci. Comput. 48, 52–69 (2011)

    Article  MathSciNet  Google Scholar 

  21. Dong, J., Li, D.F.: Well-balanced nonstaggered central schemes based on hydrostatic reconstruction for the shallow water equations with Coriolis forces and topography. Math. Methods Appl. Sci. 44, 1358–1376 (2021)

    Article  MathSciNet  Google Scholar 

  22. Fjordholm, U.S., Mishra, S., Tadmor, E.: Well-balanced and energy stable schemes for the shallow water equations with discontinuous topography. J. Comput. Phys. 230, 5587–5609 (2011)

    Article  MathSciNet  Google Scholar 

  23. Gascón, L., Corderán, J.M.: Construction of second-order TVD schemes for nonhomogeneous hyperbolic conservation laws. J. Comput. Phys. 172, 261–297 (2001)

    Article  MathSciNet  Google Scholar 

  24. Gottlieb, S., Ketcheson, D., Shu, C.-W.: Strong stability preserving Runge-Kutta and multistep time discretizations,. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ (2011)

    Book  Google Scholar 

  25. Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43, 89–112 (2001)

    Article  MathSciNet  Google Scholar 

  26. Goutal, N., Maurel, F.: Proceedings of the second workshop on dam-break wave simulation, techreport HE-43/97/016/A, Electricité de France, Département Laboratoire National d’Hydraulique, Groupe Hydraulique Fluviale (1997)

  27. Klingenberg, C., Kurganov, A., Liu, Y., Zenk, M.: Moving-water equilibria preserving HLL-type schemes forthe shallow water equations, Commun. Math. Res. 36, 247–271 (2020)

    MathSciNet  MATH  Google Scholar 

  28. Kurganov, A.: Finite-volume schemes for shallow-water equations. Acta Numer. 27, 289–351 (2018)

    Article  MathSciNet  Google Scholar 

  29. Kurganov, A., Levy, D.: Central-upwind schemes for the Saint-Venant system, M2AN Math. Model. Numer. Anal. 36, 397–425 (2002)

    Article  MathSciNet  Google Scholar 

  30. Kurganov, A., Lin, C.-T.: On the reduction of numerical dissipation in central-upwind schemes, Commun. Comput. Phys. 2, 141–163 (2007)

    MathSciNet  MATH  Google Scholar 

  31. Kurganov, A., Liu, Y., Xin, R.: Well-balanced path-conservative central-upwind schemes based on flux globalization, Submitted. Preprint available at https://sites.google.com/view/alexander-kurganov/publications

  32. Kurganov, A., Liu, Y., Zeitlin, V.: A well-balanced central-upwind scheme for the thermal rotating shallow water equations. J. Comput. Phys. 411, 109414 (2020)

    Article  MathSciNet  Google Scholar 

  33. Kurganov, A., Liu, Y., Zeitlin, V.: Interaction of tropical cyclone-like vortices with sea-surface temperature anomalies and topography in a simple shallow-water atmospheric model. Phys. Fluids 33, 106606 (2021)

    Article  Google Scholar 

  34. Kurganov, A., Liu, Y., Zeitlin, V.: Thermal versus isothermal rotating shallow water equations: comparison of dynamical processes by simulations with a novel well-balanced central-upwind scheme. Geophys. Astrophys. Fluid Dyn. 115, 125–154 (2021)

    Article  MathSciNet  Google Scholar 

  35. Kurganov, A., Noelle, S., Petrova, G.: Semi-discrete central-upwind schemes for hyperbolic conservation laws and Hamilton-Jacobi equations. SIAM J. Sci. Comput. 23, 707–740 (2001)

    Article  MathSciNet  Google Scholar 

  36. Kurganov, A., Petrova, G.: A second-order well-balanced positivity preserving central-upwind scheme for the Saint-Venant system. Commun. Math. Sci. 5, 133–160 (2007)

    Article  MathSciNet  Google Scholar 

  37. Kurganov, A., Tadmor, E.: New high resolution central schemes for nonlinear conservation laws and convection-diffusion equations. J. Comput. Phys. 160, 241–282 (2000)

    Article  MathSciNet  Google Scholar 

  38. LeFloch, P.G.: Hyperbolic systems of conservation laws, in The theory of classical and nonclassical shock waves, Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel (2002)

  39. LeFloch, P.G.: Graph solutions of nonlinear hyperbolic systems. J. Hyperbolic Differ. Equ. 1, 643–689 (2004)

    Article  MathSciNet  Google Scholar 

  40. LeFloch, P.G., Thanh, M.D.: A Godunov-type method for the shallow water equations with discontinuous topography in the resonant regime. J. Comput. Phys. 230, 7631–7660 (2011)

    Article  MathSciNet  Google Scholar 

  41. Lie, K.-A., Noelle, S.: On the artificial compression method for second-order nonoscillatory central difference schemes for systems of conservation laws. SIAM J. Sci. Comput. 24, 1157–1174 (2003)

    Article  MathSciNet  Google Scholar 

  42. Liu, X., Chen, X., Jin, S., Kurganov, A., Yu, H.: Moving-water equilibria preserving partial relaxation scheme for the Saint-Venant system. SIAM J. Sci. Comput. 42, A2206–A2229 (2020)

    Article  MathSciNet  Google Scholar 

  43. Martinez-Gavara, A., Donat, R.: A hybrid second order scheme for shallow water flows. J. Sci. Comput. 48, 241–257 (2011)

    Article  MathSciNet  Google Scholar 

  44. Nessyahu, H., Tadmor, E.: Nonoscillatory central differencing for hyperbolic conservation laws. J. Comput. Phys. 87, 408–463 (1990)

    Article  MathSciNet  Google Scholar 

  45. Noelle, S., Xing, Y., Shu, C.W.: High-order well-balanced finite volume weno schemes for shallow water equation with moving water. J. Comput. Phys. 226, 29–58 (2007)

    Article  MathSciNet  Google Scholar 

  46. Parés, C.: Path-conservative numerical methods for nonconservative hyperbolic systems. In: Numerical Methods for Balance Laws, vol. 24, Quad. Mat. Dept. Math. Seconda Univ. Napoli, Caserta, pp. 67–121 (2009)

  47. Pimentel-García, E., Castro, M.J., Chalons, C., Morales de Luna, T., Parés, C.: In-cell discontinuous reconstruction path-conservative methods for non conservative hyperbolic systems—second-order extension J. Comput. Phys., 459 (2022). Paper No. 111152, 35 pp

  48. Ricchiuto, M.: An explicit residual based approach for shallow water flows. J. Comput. Phys. 280, 306–344 (2015)

    Article  MathSciNet  Google Scholar 

  49. Schneider, K.A., Gallardo, J.M., Balsara, D.S., Nkonga, B., Parés, C.: Multidimensional approximate Riemann solvers for hyperbolic nonconservative systems. Applications to shallow water systems. J. Comput. Phys., 444 (2021). Paper No. 110547, 49 pp

  50. Sweby, P.K.: High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 21, 995–1011 (1984)

    Article  MathSciNet  Google Scholar 

  51. Vázquez-Cendón, M.E.: Improved treatment of source terms in upwind schemes for the shallow waterequations in channels with irregular geometry. J. Comput. Phys. 148, 497–526 (1999)

    Article  MathSciNet  Google Scholar 

  52. Xing, Y.: Numerical methods for the nonlinear shallow water equations, in Handbook of numerical methods for hyperbolic problems, vol. 18 of Handb. Numer. Anal., Elsevier/North-Holland, Amsterdam, pp. 361–384 (2017)

Download references

Funding

The work of A. Kurganov was supported in part by NSFC grants 12171226 and 12111530004, and by the fund of the Guangdong Provincial Key Laboratory of Computational Science and Material Design (No. 2019B030301001).

Author information

Authors and Affiliations

  1. Department of Mathematics, Southern University of Science and Technology, Shenzhen, 518055, China

    Yangyang Cao, Yongle Liu & Ruixiao Xin

  2. Department of Mathematics, SUSTech International Center for Mathematics and Guangdong Provincial Key Laboratory of Computational Science and Material Design, Southern University of Science and Technology, Shenzhen, 518055, China

    Alexander Kurganov

Authors
  1. Yangyang Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Alexander Kurganov
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yongle Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ruixiao Xin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yongle Liu.

Ethics declarations

Competing Interests

The authors have not disclosed any competing interests.

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cao, Y., Kurganov, A., Liu, Y. et al. Flux Globalization Based Well-Balanced Path-Conservative Central-Upwind Schemes for Shallow Water Models. J Sci Comput 92, 69 (2022). https://doi.org/10.1007/s10915-022-01912-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-01912-w

Keywords

Mathematics Subject Classification