Abstract
Curvilinear, multiblock summation-by-parts finite difference operators with the simultaneous approximation term method provide a stable and accurate framework for solving the wave equation in second order form. That said, the standard method can become arbitrarily stiff when characteristic boundary conditions and nonlinear interface conditions are used. Here we propose a new technique that avoids this stiffness by using characteristic variables to “upwind” the boundary and interface treatment. This is done through the introduction of an additional block boundary displacement variable. Using a unified energy, which expresses both the standard as well as characteristic boundary and interface treatment, we show that the resulting scheme has semidiscrete energy stability for the scalar anisotropic wave equation. The theoretical stability results are confirmed with numerical experiments that also demonstrate the accuracy and robustness of the proposed scheme. The numerical results also show that the characteristic scheme has a time step restriction based on standard wave propagation considerations and not the boundary closure.







Similar content being viewed by others
Notes
The free parameter \(x_1=0.70127127127127\) is used for \(2p = 6\).
References
Almquist, M., Dunham, E.M.: Non-stiff boundary and interface penalties for narrow-stencil finite difference approximations of the laplacian on curvilinear multiblock grids. J. of Comput. Phys. 408, 109–294 (2020). https://doi.org/10.1016/j.jcp.2020.109294
Almquist, M., Dunham, E.M.: Elastic wave propagation in anisotropic solids using energy-stable finite differences with weakly enforced boundary and interface conditions. J. of Comput. Phys. 424, 109–842 (2021). https://doi.org/10.1016/j.jcp.2020.109842
Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: A fresh approach to numerical computing. SIAM review 59(1), 65–98 (2017). https://doi.org/10.1137/141000671
Carpenter, M.H., Gottlieb, D., Abarbanel, S.: Time-stable boundary conditions for finite-difference schemes solving hyperbolic systems: Methodology and application to high-order compact schemes. J. of Comput. Phys. 111(2), 220–236 (1994). https://doi.org/10.1006/jcph.1994.1057
Carpenter, M.H., Kennedy, C.A.: Fourth-order 2N-storage Runge-Kutta schemes. Tech. Rep. NASA TM-109112, National Aeronautics and Space Administration, Langley Research Center, Hampton, VA (1994)
Carpenter, M.H., Nordström, J., Gottlieb, D.: A stable and conservative interface treatment of arbitrary spatial accuracy. J. of Comput. Phys. 148(2), 341–365 (1999). https://doi.org/10.1006/jcph.1998.6114
Duru, K., Allison, K.L., Rivet, M., Dunham, E.M.: Dynamic rupture and earthquake sequence simulations using the wave equation in second-order form. Geophys. J. Int. 219(2), 796–815 (2019). https://doi.org/10.1093/gji/ggz319
Erickson, B.A., Jiang, J., Barall, M., Lapusta, N., Dunham, E.M., Harris, R., Abrahams, L.S., Allison, K.L., Ampuero, J.P., Barbot, S., Cattania, C., Elbanna, A., Fialko, Y., Idini, B., Kozdon, J.E., Lambert, V., Liu, Y., Luo, Y., Ma, X., Mckay, M.B., Segall, P., Shi, P., van den Ende, M., Wei, M.: The community code verification exercise for simulating sequences of earthquakes and aseismic slip (seas). Seismol. Res. Lett. 91, 874–890 (2020). https://doi.org/10.1785/0220190248
Hicken, J.E., Zingg, D.W.: Summation-by-parts operators and high-order quadrature. J. of Comput. and Appl. Math. 237(1), 111–125 (2013). https://doi.org/10.1016/j.cam.2012.07.015
Kopriva, D.A.: Metric identities and the discontinuous spectral element method on curvilinear meshes. J. of Sci. Comput. 26(3), 301–327 (2006). https://doi.org/10.1007/s10915-005-9070-8
Kozdon, J.E., Dunham, E.M., Nordström, J.: Interaction of waves with frictional interfaces using summation-by-parts difference operators: Weak enforcement of nonlinear boundary conditions. J. of Sci. Comput. 50(2), 341–367 (2012). https://doi.org/10.1007/s10915-011-9485-3
Kozdon, J.E., Wilcox, L.C.: Stable coupling of nonconforming, high-order finite difference methods. SIAM J. on Sci. Comput. 38(2), A923–A952 (2016). https://doi.org/10.1137/15M1022823
Kreiss, H., Oliger, J.: Comparison of accurate methods for the integration of hyperbolic equations. Tellus 24(3), 199–215 (1972). https://doi.org/10.1111/j.2153-3490.1972.tb01547.x
Kreiss, H., Scherer, G.: Finite element and finite difference methods for hyperbolic partial differential equations. In: Mathematical aspects of finite elements in partial differential equations; Proceedings of the Symposium, pp. 195–212. Madison, WI (1974). https://doi.org/10.1016/b978-0-12-208350-1.50012-1
Kreiss, H., Scherer, G.: On the existence of energy estimates for difference approximations for hyperbolic systems. Tech. rep., Department of Scientific Computing, Uppsala University (1977)
Mattsson, K.: Summation by parts operators for finite difference approximations of second-derivatives with variable coefficients. Journal of Scientific Computing 51(3), 650–682 (2012). https://doi.org/10.1007/s10915-011-9525-z
Mattsson, K., Carpenter, M.H.: Stable and accurate interpolation operators for high-order multiblock finite difference methods. SIAM J. on Sci. Comput. 32(4), 2298–2320 (2010). https://doi.org/10.1137/090750068
Mattsson, K., Ham, F., Iaccarino, G.: Stable and accurate wave-propagation in discontinuous media. J. of Comput. Phys. 227(19), 8753–8767 (2008). https://doi.org/10.1016/j.jcp.2008.06.023
Mattsson, K., Ham, F., Iaccarino, G.: Stable boundary treatment for the wave equation on second-order form. J. of Sci. Comput. 41(3), 366–383 (2009). https://doi.org/10.1007/s10915-009-9305-1
Mattsson, K., Nordström, J.: Summation by parts operators for finite difference approximations of second derivatives. J. of Comput. Phys. 199(2), 503–540 (2004). https://doi.org/10.1016/j.jcp.2004.03.001
Mattsson, K., Parisi, F.: Stable and accurate second-order formulation of the shifted wave equation. Commun. in Comput. Phys. 7(1), 103 (2010). https://doi.org/10.4208/cicp.2009.08.135
Nordström, J.: A roadmap to well posed and stable problems in computational physics. J. of Sci. Comput. 71(1), 365–385 (2017). https://doi.org/10.1007/s10915-016-0303-9
Olsson, P.: Summation by parts, projections, and stability. I. Math. of Comput. 64(211), 1035–1065 (1995). https://doi.org/10.2307/2153482
Olsson, P.: Summation by parts, projections, and stability. II. Math. of Comput. 64(212), 1473–1493 (1995). https://doi.org/10.2307/2153366
Roache, P.: Verification and validation in computational science and engineering, 1st edn. Hermosa Publishers, Albuquerque, NM (1998)
Strand, B.: Summation by parts for finite difference approximations for d/dx. J. of Comput. Phys. 110(1), 47–67 (1994). https://doi.org/10.1006/jcph.1994.1005
Strand, B.: Summation by parts for finite difference approximations for \(d/dx\). J. of Comput. Phys. 110(1), 47–67 (1994). https://doi.org/10.1006/jcph.1994.1005
Virta, K., Mattsson, K.: Acoustic wave propagation in complicated geometries and heterogeneous media. J. of Sci. Comput. 61(1), 90–118 (2014). https://doi.org/10.1007/s10915-014-9817-1
Wang, S., Virta, K., Kreiss, G.: High order finite difference methods for the wave equation with non-conforming grid interfaces. J. of Sci. Comput. 68(3), 1002–1028 (2016). https://doi.org/10.1007/s10915-016-0165-1
Acknowledgements
We thank the two anonymous reviewers whose insightful feedback substantially improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
B.A.E. was supported by National Science Foundation Awards EAR-1547603 and EAR-1916992
J.E.K. was supported by National Science Foundation Award EAR-1547596
T.H. was supported by National Science Foundation EAR-1916992
The views expressed in this document are those of the authors and do not reflect the official policy or position of the Department of Defense or the U.S. Government.
Approved for public release; distribution unlimited.
Appendices
Appendix A Definition of Two-Dimensional SBP Operators
As an example of how to construct multidimensional SBP operators, we consider the two dimensional SBP finite difference operators. We describe the operators on the reference block \(\hat{B} = [0,1] \times [0,1]\), where faces 1 and 2 are the right and left faces with faces 3 and 4 being the top and bottom faces, respectively. For simplicity we let the domain \(\hat{B}\) be discretized with an \((N+1) \times (N+1)\) grid points with the grid nodes located at \({\left\{ {{\varvec{\xi }}}\right\} }_{kl} = (kh, lh)\) for \(0 \le k,l \le N\) with \(h = 1/N\). The projection of u onto the grid is denoted \({{\varvec{\tilde{u}}}}\), where \({\left\{ {{\varvec{\tilde{u}}}}\right\} }_{kl} \approx u(kh, lh)\) and is stored as a vector with with \(\xi _1\) being the fastest index; see (8). With this, the volume norm matrix can be written as
We define the face restriction operators as
where the \({{\varvec{{I}}}}\) is the \((N+1) \times (N+1)\) identity matrix. More generally the restriction to a single grid line in the \(\xi _1\) and \(\xi _2\) directions, respectively, are
In order to construct \({{\varvec{\tilde{ A}}}}_{ii}^{(C)}\), no summation over i, we construct individual one-dimensional second derivative matrices for each grid line with varying coefficients C and place them in the correct block; expanding a single second derivative matrix with the tensor product and the identity matrix only works in the constant coefficient case. To do this it is useful to define \({{\varvec{\tilde{C}}}}\) as the projection of C onto the grid with the coefficients along the individual grid lines being
The second derivative operators are the sum of the operators along each grid line
and a tensor product is used for the mixed derivative operators
The boundary derivatives parallel to a face are given by the first derivative operator \({{\varvec{{D}}}}_{1}\) and those perpendicular with the boundary derivative operators from the SBP definition 2:
Appendix B Proof of Theorem 7
To show that energy (105) is positive we need the following definition from [16, Definition 2.4]:
The remainder matrix \({{\varvec{\tilde{ R}}}}_{ij}^{(c)}\) is symmetric positive semidefinite if the coefficient c is always positive; the remainder matrix is zero when \(i \ne j\). The remainder matrix can be further decomposed using the borrowing lemma from [1, Lemma 1]:
Here the matrix \({{\varvec{\tilde{ S}}}}_{ii}^{(c)}\) (no summation over i) is a positive semidefinite and the matrix \({{\varvec{{\bar{\varDelta }}}}}_{i}^{f} = {{\varvec{{\bar{B}}}}}_{i}^{f} - {{\varvec{{\bar{D}}}}}_{i}^{f}\) is the difference between the boundary derivative matrix from \({{\varvec{\tilde{ D}}}}_{ii}\) (no summation over i) and the first derivative matrix \({{\varvec{\tilde{ D}}}}_{i}\) at the boundary. Each element of the diagonal matrix \({{\varvec{{C}}}}^{f,min}\) is the minimum value of c in the \(m_{b}\) points orthogonal to the boundary where \(m_{b}\) depends on the order of accuracy of the SBP operator. The positive constant \(\zeta ^f = h^f_{\bot } \bar{\zeta }\) where \(h^{f}_{\bot }\) is the grid spacing orthogonal to the face and \(\bar{\zeta }\) is a constant which depends on the SBP operator. The \((m_{b}, \bar{\zeta })\) values used for the operators in this paper are given in Table 3; see [1, Table 1].
Since \({{\varvec{\tilde{ H}}}}\) is diagonal and positive, it is clear that for any face f
where \(\theta ^{f}\) is the value of the \({\left\{ {{\varvec{H}}}\right\} }_{00}\) where \({{\varvec{H}}}\) is the norm matrix orthogonal to the face. It then follows that
where the factor of 1/d is needed to avoid over counting corners and, when \(d = 3\), edges. Since the coefficient matrix \(C_{ij}\) is positive definite, this can be extended to included the variable coefficients:
We now turn to considering the discrete block energy (105). The first term satisfies
because it is in quadratic form and \({{\varvec{\tilde{ H}}}}\) and \({{\varvec{\tilde{ \rho }}}}\) are diagonal, positive matrices. The remaining terms will be shown to combine in a manner that is also positive semidefinite.
Combing relations (138), (139), and (142) we have that
We now considering the face term of the discrete block energy (105). Defining \({{\varvec{\delta }}}^{f}_{u} = {{\varvec{u}}}^{*f} - {{\varvec{u}}}^{f}\) and using the definition of \({{\varvec{\hat{\tau }}}}^{f}\) and \({{\varvec{\hat{T}}}}^{f}\) in (107) gives
It is useful to note that \({{\varvec{\hat{T}}}}\) can be rewritten using \({{\varvec{{\bar{\varDelta }}}}}^{f}_{k}\) as
this follows because only when \(f \in (2j, 2j-1)\) is \({{\varvec{{\bar{B}}}}}^{f}_{j} \ne {{\varvec{{\bar{D}}}}}^{f}_{j}\). Using this along with the definition of \({{\varvec{{X}}}}^{f}\) in (106) leads to,
where \(k = \left\lceil {\frac{f}{2}}\right\rceil \).
Returning to the remaining terms of block energy (105), we use (144) and (147) to write
If we choose
then we have that
where we have used that \(\hat{n}^{f}_{i} {{\varvec{{\hat{C}}}}}_{ij}^{f} \hat{n}^{f}_{j} = {{\varvec{{\hat{C}}}}}_{kk}^{f}\) with \(k = \left\lceil {\frac{f}{2}}\right\rceil \) (no summation over k). Though a similar transformation could be used on the first summation it is not needed and complicates the analysis that follows. Returning to (148) then gives with (150)
where we have used that \({{\varvec{{\hat{C}}}}}_{kk}^{f} = \hat{n}^{f}_{k} {{\varvec{{\hat{C}}}}}_{kk}^{f} \hat{n}_{k}^{t}\) (no summation over k) and \({{\varvec{{\hat{C}}}}}_{kk}^{f,\min } {{\varvec{{P}}}}^{f} = {{\varvec{{C}}}}_{kk}^{f}\) (no summation over k). Since this expression is in quadratic form, it is non-negative and the when combine with (143) shows that the block energy (105) is non-negative.
Appendix C Non-Characteristic Boundary and Interface Treatment
The standard approach for SBP-SAT for Dirichlet (78b), and characteristic boundaries (78c) as well as computational and nonlinear interfaces from Virta and Mattsson [28] and Duru et al. [7] are presented in the notation of this paper; Neumann boundary treatment is the same as the characteristic boundary treat with \(R = 1\).
1.1 C.1 Dirichlet Boundary Conditions
When block face f is on a Dirichlet boundary (87b) then the numerical fluxes are chosen to be
Using these numerical fluxes, the face energy rate of change (109) is
which with \(g_{D} = 0\) gives \(\dot{\mathcal {E}}^{f} = 0\) and does not lead to energy growth.
1.2 C.2 Characteristic (and Neumann) Boundary Conditions
In order to define the standard treatment of characteristic boundary conditions (78c), it is useful to solve (78c) for \(\tau \):
with \(\alpha = -Z (1 - R) / (R + 1) \le 0\) and \(\nu = 1 / (R + 1)\). We note again that the Neumann boundary condition is attained when \(R = 1\) in which case \(\alpha = 0\) and \(\nu = 1\). With this, if block face f is on a characteristic boundary then the numerical fluxes are chosen to be
where the parameters \({{\varvec{{\hat{\alpha }}}}}\) and \({{\varvec{{\hat{\nu }}}}}\) are diagonal matrices of \(S_{J}^{f} \alpha \) and \(S_{J}^{f} \nu \) evaluated at each point on face f. Using these numerical fluxes in (109) give
With \(g_{C} = 0\) we then have that \(\dot{\mathcal {E}}^{f} \le 0\) and there is no energy growth due to the characteristic boundary treatment; equality is obtained in the Neumann case.
1.3 C.3 Computational Interface
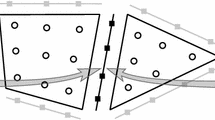
For computational interfaces (e.g., interfaces between blocks in the domains that have been introduced to mesh to either a material interface and/or needed in the mesh generation) continuity of displacement and traction need to be enforced. That is, across the interface it is required that
Here the superscript ± denotes the value on either side of the interface with the unit normal \({\varvec{n}}^{\pm }\) is taken to be outward to each side of the interface, i.e., \({\varvec{n}}^{-} = -{\varvec{n}}^{+}\). The standard approach to enforcing this is to choose the numerical flux to be the average of the values on the two sides of the interface,
the minus sign in \({{\varvec{\hat{\tau }}}}^{*f^{-}}\) is due to the unit normals being equal and opposite. Here the two blocks connected across the interface are \(B^{\pm }\) through faces \(f^{\pm }\).
The face energy rate of change (109) for computational interfaces is then
Adding the two sides of the interface together gives
and energy stability results.
1.4 C.4 Nonlinear Interface Condition
The approach Duru et al. [7] for nonlinear interfaces is to define the sliding velocity \(V^{\pm f}\) directly from the particle velocities on the grid and then the traction \(\tau ^{f}\) is defined directly from the nonlinear function so the numerical fluxes are
The face energy rate of change (109) for a nonlinear interface is then
Adding the two sides of the interface together gives
where we have used that \({{\varvec{V}}}^{f^{-}} = -{{\varvec{V}}}^{f^{+}}\) and the fact that \(V \hat{F}(V) \ge 0\).
Appendix D Nonlinear Interface Root Finding Problem
In general, evaluating \(\mathcal {Q}^{\pm }\) for a nonlinear condition \(\tau ^{\pm } = F\left( V^{\pm }\right) \) requires solving a nonlinear root finding problem. In particular, using the characteristic variables \(w^{\pm }\) a root finding problem for \(V^{\pm }\) is solved after which \(\mathcal {Q}^{\pm }\) can be determined.
Recall that force balance, \(\tau ^{-} = -\tau ^{+}\), and the fact that \(V^{-} = -V^{+}\) implies that \(\tau ^{-} = -F\left( V^{+}\right) \). Using this we can compute the \(Z^{\pm }\) weighted-average
Expressing \(\tau ^{\pm }\) in terms of \(\mathcal {Q}^{\pm }\) and \(w^{\pm }\), see (93b), then gives
The sliding velocity \(V^{+}\) can be written in terms of the characteristic variables using (93a):
Using this, we can rewrite (165) as
This expression can be more compactly written by defining
which depends only on the characteristic variables propagating into the interface and is the traction that would result if the interface were a computational interface; seen by using (92) in (93b). We can now write the final form of the root finding problem as
where \(\eta = Z^{+}Z^{-} / (Z^{+} + Z^{-})\) is known as the radiation damping coefficient. Once this nonlinear system is solved for \(V^{+}\) all other quantities can be determined using (93). When numerically solving (169) it is useful to realize that \({{\,\mathrm{sgn}\,}}\left( V^{+}\right) = {{\,\mathrm{sgn}\,}}\left( \tau _{l}^{+}\right) \) and that the root can be bracketed: \(\left| V^{+}\right| \in \left[ 0, F^{-1}\left( \tau _{l}^{+}\right) \right] \).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Erickson, B.A., Kozdon, J.E. & Harvey, T. A Non-Stiff Summation-By-Parts Finite Difference Method for the Scalar Wave Equation in Second Order Form: Characteristic Boundary Conditions and Nonlinear Interfaces. J Sci Comput 93, 17 (2022). https://doi.org/10.1007/s10915-022-01961-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-022-01961-1