Numerical Factorization of Propagation Operator for Hyperbolic Equations and Application to One-way, True Amplitude One-way Equations and Bremmer Series

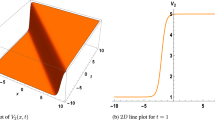
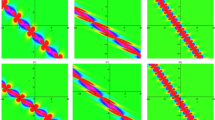
Abstract

This paper presents a purely numerical factorization of the propagation operator for a generic hyperbolic equation, based on the work of Towne & Colonius in 2015, that does not require heavy analytical development. This method is applied to form one-way equations with the objective of computing the propagation of waves inside a medium. The main advantage of this formulation is that pseudo eigenvectors and eigenvalues matrices are built, leading to the possibility to use the one-way equations into a true amplitude formalism and/or inside a Bremmer series. These two methods allow an extension of the domain of application of the one-way equations when the medium of propagation presents variations along the privileged direction. In particular, these formulations allow to take into account the phenomena of reflection and refraction of the incident wave. Finally numerical results are presented on different 2D situations based on the linearized Euler equations and compared to the results obtained with a full wave resolution. The issues of both the accuracy and the requirements in computational resources of the one-way resolution are also addressed.

Appendices

Some Background About Pseudo-Differential Operators

Some definitions and basic features of the pseudo-differential operators theory [1, 24, 40] will be reminded (the proofs can be found in these references, especially in the latter one) and a brief description of them will be made. These operators rely upon the Fourier transform defined as:

$$\begin{aligned} ({\mathcal {F}}f)(\xi ) = \int f(y)e^{-i\xi y}dy \; , \end{aligned}$$

(77)

with $\xi$ the Fourier dual variable of y.

Then, we proceed to a “classical’ quantization that consists in linking a function of space-time variables and their Fourier associates to an operator. Hence, P is a pseudo-differential operator if

$$\begin{aligned} P f\left( y\right) = \frac{1}{\left( 2\pi \right) ^2}\int \sigma \left( P\right) \left( y,\xi \right) \;\left( {\mathcal {F}} f\right) \left( \xi \right) e^{i\xi y}d\xi \; , \end{aligned}$$

(78)

with $\sigma (P)(y,\xi )$ the symbol of the operator P. This symbol is of class $S^m$ with $m\in {\mathbb {Z}}$ if it is a smooth function of y and $\xi$ that satisfies the condition that for any indices $\left( \alpha , \beta \right) \in {\mathbb {Z}}^2{}$, there exists a constant C such that:

$$\begin{aligned} \left| \partial _y^\alpha \partial _\xi ^\beta \sigma \left( P\right) \left( y,\xi \right) \right| \le C(1+|\xi |)^{m-|\beta |} \; . \end{aligned}$$

(79)

Thus, if we take as an example a simple pseudo-differential operator, a derivative in y:

$$\begin{aligned} P = \frac{\partial }{\partial y} \; , \end{aligned}$$

(80)

its associated symbol of class $S^1$ will be:

$$\begin{aligned} \sigma (P) = i\xi \; . \end{aligned}$$

(81)

From here on out, the symbol of a pseudo-differential operator P will be denoted by its lower-case letter p. In the next three paragraphs, three rules that are inherent to the operators and that will be of interest for the new formulation of the One-Way method will be detailed: the asymptotic expansion of a symbol, the composition and the parametrix rule.

Asymptotic expansion of a symbol Let $p_j \in S^{M_j}$ be a symbol of operator of order $M_j$ with $\lim \limits _{j \rightarrow +\infty } M_j = - \infty$. Then, there exists another symbol $p \in S^{M_0}$ such that, for any $N>0$:

$$\begin{aligned} p - \sum \limits _{j=0}^{N-1}p_j \in S^{M_N} \; , \end{aligned}$$

(82)

which allows to write:

$$\begin{aligned} p \sim \sum \limits _{j \ge 0}p_j \; . \end{aligned}$$

(83)

The function $p_0$ will be called the principal symbol of p as it is the symbol of higher order in this asymptotic expansion.

Composition rule Let P and Q be two pseudo-differential operators of symbol $\sigma (P) = p$ and $\sigma (Q) = q$ and of order m and n, respectively (i.e. $P \in OPS^m, \; Q \in OPS^n$). Their combination will be another pseudo-differential operator of order $m+n$. The symbol of this operator, PQ, is denoted $p\#q$ and its asymptotic expansion is:

$$\begin{aligned} p\#q(y,\xi )&\sim \overset{\infty }{\underset{k=0}{\sum }} \frac{1}{k!} \, \partial _\xi ^k p(y,\xi ) \; \partial _y^k q(y,\xi ) \sim p(y,\xi ) \; q(y,\xi )\nonumber \\&\qquad + \partial _\xi p(y,\xi ) \; \partial _y q(y,\xi ) + r(y,\xi ) \; , \end{aligned}$$

(84)

where $r(y,\xi )$ is a symbol of order $m+n-2$. We can deduce from this relation that the principal symbol of PQ is the product of the symbols p and q.

Parametrix rule Let $P \in OPS^m$ and $Q \in OPS^{-m}$ be two pseudo-differential operators. The operator Q will be a parametrix of P if the following relation is valid:

$$\begin{aligned} PQ = I + R \; , \end{aligned}$$

(85)

with I the identity operator and R a pseudo-differential operator of order $n < 0$. This operator R can be seen as a residual and it can be truncated at any order.

Application to Systems of Two Equations

In systems of two equations, each block of the matrices split along the $+$ and − subscripts contains only one pseudo-differential operator. Therefore, in the right One-Way formalism, the matrices $Z_{--}^r$, $Z_{-+}^r$, $U_{--}$ and $U_{-+}$ are composed of only one operator of which, we will assume, we ignore the analytical expression.

First, $U_{--}$ is assumed to be a pseudo-differential operator of order p and $U_{--}^{-1}$ is its parametrix denoted $A \in OPS^{-p}$. Moreover, the operator $U_{-+}$ is assumed to be of order n and will be denoted for readability reasons $B \in OPS^{n}$. It leads, according to Eq. (35), to the fact that the product $\left( {Z_{--}^r}\right) ^{-1}Z_{-+}^r$ is of order $m = -p+n$ and it will be denoted $C \in OPS^{m}$. This composition can then be written in terms of symbols:

$$\begin{aligned} c = a \,\#\, b \;. \end{aligned}$$

(86)

Now, the asymptotic expansion of the symbols and the composition rules stated above in Eqs. (83) and (84) yield:

$$\begin{aligned} c_0 + c_1 + r_c = a_0b_0 + \partial _\xi a_0 \partial _x b_0 + a_0b_1 + a_1b_0 + \partial _\xi a_0 \partial _x b_1 + \partial _\xi a_1 \partial _x b_0 + r_{ab} \; , \end{aligned}$$

(87)

where $r_c$ and $r_{ab}$ are symbols of order $m-2$ and represent the residuals of the asymptotic expansion of c and the composition of $a \,\#\, b$ respectively. If we sort these symbols by order, we obtain:

$$\begin{aligned} \left\{ \begin{aligned} c_0&= a_0b_0 \,\in S^m \\ c_1&= \partial _\xi a_0 \partial _x b_0 + a_0b_1 + a_1b_0 \,\in S^{m-1} \\ r_c&= \partial _\xi a_0 \partial _x b_1 + \partial _\xi a_1 \partial _x b_0 + r_{ab}\,\in S^{m-2} \end{aligned} \right. \; . \end{aligned}$$

(88)

By keeping the first relation, we can deduce that the principal symbol of the product $\left( {Z_{--}^r}\right) ^{-1}Z_{-+}^r$ is equal to the one of $U_{--}^{-1}U_{-+}$. Moreover, as U is the left eigenvectors matrix of M, $U_{--}$ and $U_{-+}$ are the two components of the same eigenvector. This eigenvector can be normalized arbitrarily by setting one of these components to 1, for example. If we choose, for instance, to set $U_{-+}$ to 1, the first equation of the system (88) becomes:

$$\begin{aligned} c_0 = a_0 \; . \end{aligned}$$

(89)

If we put this equation back in term of operators:

$$\begin{aligned} \left( {Z_{--}^r}\right) ^{-1}Z_{-+}^r = U_{--}^{-1} \; . \end{aligned}$$

(90)

From this relation, we can get the second component of the eigenvector. As there is no uniqueness in the choice of normalization made (we can either set $U_{-+}$ or $U_{--}$ to 1 or another choice of normalization), it will impact on the lower orders of Eq. (88). It means that even if the relation of the principal symbols is respected, some guesses will be more accurate than others for the lower order relations.

In order to get the second eigenvector of U, we need to reverse the Towne-Colonius method and to track the leftgoing waves. It can be done by reversing the recursion relation of system (32) as follows:

$$\begin{aligned} \begin{pmatrix} {\mathbf {0}}\\ \varvec{\phi }_-^{N_\beta } \end{pmatrix} = \overset{N_\beta -1}{\underset{j=0}{\prod }} \left( {\mathbf {M}}-i\beta _+^j{\mathbf {I}}\right) ^{-1}\left( {\mathbf {M}} - i\beta _-^j{\mathbf {I}}\right) \begin{pmatrix} \varvec{\phi }_+\\ \varvec{\phi }_- \end{pmatrix} \; . \end{aligned}$$

(91)

In this way, the non-reflection matrix is set to erase the rightgoing waves while keeping the leftgoing ones. This equation gives us a new relation between the two components of the remaining eigenvector. Similarly as before but in the other direction, with a sufficient number of $\beta _\pm$ (the same as before), we can write:

$$\begin{aligned} \left( {Z_{++}^l}\right) ^{-1}Z_{+-}^l \approx U_{++}^{-1}U_{+-} \; . \end{aligned}$$

(92)

By using the same strategy of normalization as before, we can set $U_{++} = 1$ which means:

$$\begin{aligned} \left( {Z_{++}^l}\right) ^{-1}Z_{+-}^l = U_{+-} \; . \end{aligned}$$

(93)

We now have access to an approximation of the whole U matrix and consequently to approximations of the matrices V and D. Now, we only have to solve the system of Eq. (17).