Skip to main content
Springer Nature Link
Log in

A Weak Galerkin Finite Element Method Can Compute Both Upper and Lower Eigenvalue Bounds

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

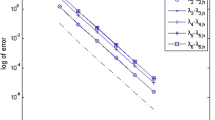
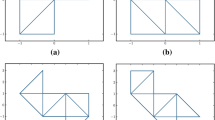
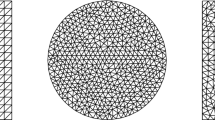
In this paper, we observe an interesting phenomenon for a weak Galerkin (WG) approximation of eigenvalue problems, that is, we may obtain good approximations for exact eigenvalues from below or above, only through adjusting the global penalty parameter. Based on this observation, a high accuracy algorithm for computing eigenvalues is designed to yield higher convergence order with lower expenses. Some new techniques are developed to analyze upper and lower bound properties of eigenvalues. Numerical results supporting our theory are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability

Enquiries about data availability should be directed to the authors.

References

  1. Adams, R.: Sobolev spaces. In: Pure and Applied Mathematics, Vol. 65. Academic Press [Harcourt Brace Jovanovich, Publishers], New York, London (1975)

  2. Armentano, M., Durán, R.: Asymptotic lower bounds for eigenvalues by nonconforming finite element methods. Electron. Trans. Numer. Anal. 17, 93–101 (2004)

    MathSciNet  MATH  Google Scholar 

  3. Babuška, I., Osborn, J.: Finite element-Galerkin approximation of the eigenvalues and eigenvectors of selfadjoint problems. Math. Comput. 52(186), 275–297 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  4. Babuška, I., Osborn, J.: Eigenvalue problems. In: Handbook of Numerical Analysis, vol. 2, pp. 641–787. North-Holland (1991)

  5. Boffi, D.: Finite element approximation of eigenvalue problems. Acta Numer. 19, 1–120 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  6. Carstensen, C., Zhai, Q., Zhang, R.: A skeletal finite element method can compute lower eigenvalue bounds. SIAM J. Numer. Anal. 58(1), 109–124 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  7. Hu, J., Huang, Y., Lin, Q.: Lower bounds for eigenvalues of elliptic operators: by nonconforming finite element methods. J. Sci. Comput. 61(1), 196–221 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hu, J., Huang, Y., Shen, Q.: The lower/upper bound property of approximate eigenvalues by nonconforming finite element methods for elliptic operators. J. Sci. Comput. 58(3), 574–591 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Mu, L., Wang, J., Ye, X., Zhang, S.: A weak Galerkin finite element method for the Maxwell equations. J. Sci. Comput. 65(1), 363–386 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Strang, G., Fix, G.: An Analysis of the Finite Element Method. Prentice-Hall Series in Automatic Computation, Prentice-Hall Inc, Englewood Cliffs (1973)

    MATH  Google Scholar 

  11. Wang, J., Ye, X.: A weak Galerkin finite element method for second-order elliptic problems. J. Comput. Appl. Math. 241, 103–115 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  12. Wang, J., Ye, X.: A weak Galerkin mixed finite element method for second order elliptic problems. Math. Comput. 83(289), 2101–2126 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  13. Wang, J., Ye, X.: A weak Galerkin finite element method for the stokes equations. Adv. Comput. Math. 42(1), 155–174 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Yang, Y., Lin, Q., Bi, H., Li, Q.: Eigenvalue approximations from below using Morley elements. Adv. Comput. Math. 36(3), 443–450 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Yang, Y., Shih, T., Liem, C., Lü, T.: An abstract error estimate for eigenvalue finite element approximation. Math. Numer. Sin. 20(4), 359–366 (1998)

    MathSciNet  MATH  Google Scholar 

  16. Yang, Y., Zhang, Z., Lin, F.: Eigenvalue approximation from below using non-conforming finite elements. Sci. China Math. 53(1), 137–150 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  17. Zhai, Q., Xie, H., Zhang, R., Zhang, Z.: The weak Galerkin method for elliptic eigenvalue problems. Commun. Comput. Phys. 26(1), 160–191 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  18. Zhai, Q., Ye, X., Wang, R., Zhang, R.: A weak Galerkin finite element scheme with boundary continuity for second-order elliptic problems. Comput. Math. Appl. 74(10), 2243–2252 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhang, Z., Yang, Y., Chen, Z.: Eigenvalue approximation from below by Wilson’s element. Math. Numer. Sin. 29(3), 319–321 (2007)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the anonymous referees for their valuable suggestions and comments.

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. School of Mathematical Science, Tongji University, Shanghai, 200092, China

    Qigang Liang, Xuejun Xu & Liuyao Yuan

  2. Institute of Computational Mathematics, AMSS, Chinese Academy of Sciences, Beijing, 100190, China

    Xuejun Xu

Authors
  1. Qigang Liang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xuejun Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Liuyao Yuan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xuejun Xu.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors were supported by National Natural Science Foundation of China (Grant Nos. 12071350, 11871272), Shanghai Municipal Science and Technology Major Project No. 2021SHZDZX0100, and Science and Technology Commission of Shanghai Municipality.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liang, Q., Xu, X. & Yuan, L. A Weak Galerkin Finite Element Method Can Compute Both Upper and Lower Eigenvalue Bounds. J Sci Comput 93, 19 (2022). https://doi.org/10.1007/s10915-022-01986-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-01986-6

Keywords