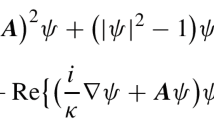Skip to main content
Springer Nature Link
Log in

Residual-Based a Posteriori Error Estimates for the Time-Dependent Ginzburg–Landau Equations of Superconductivity

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

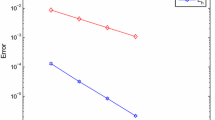
We propose and analyze residual-based a posteriori error estimator for a new finite element method for the time-dependent Ginzburg–Landau equations with the temporal gauge of superconductivity. The magnetic potential variable is approximated by \(H(\nabla \times ;\Omega )\)-conforming element and the scalar order parameter is approximated by the \(H^1(\Omega )\)-conforming element. Using the dual problem of a linearization of the original problem, we prove the reliability of the a posteriori error estimator, and an adaptive algorithm with the temporal and spatial refining and coarsening steps is then proposed. Numerical results are presented for illustrating the a posteriori error estimator and the adaptive algorithm in convex and nonconvex domains.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

Data Availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

References

  1. Tinkham, M.: Introduction to Superconductivity, 2nd edn. McGraw-Hill, New York (1996)

    Google Scholar 

  2. Li, M., Gu, J., Du, L., et al.: Time-dependent Ginzburg–Landau equations for multi-gap superconductors. Chin. Phys. B 29, 037401 (2020)

    Google Scholar 

  3. Blair, A.I., Hampshire, D.P.: Time-dependent Ginzburg–Landau simulations of the critical current in superconducting films and junctions in magnetic fields. IEEE Trans. Appl. Supercond. 28, 1–5 (2018)

    Google Scholar 

  4. Fan, J., Zhou, Y.: A regularity criterion to the time-dependent Ginzburg–Landau model for superconductivity in Rn. J. Math. Anal. Appl. 483, 123653 (2020)

    MathSciNet  MATH  Google Scholar 

  5. Lara, A., González-Ruano, C., Aliev, F.G.: Time-dependent Ginzburg–Landau simulations of superconducting vortices in three dimensions. Low Temp. Phys. 46, 316–324 (2020)

    Google Scholar 

  6. Oripov, B., Anlage, S.M.: Time-dependent Ginzburg–Landau treatment of RF magnetic vortices in superconductors: Vortex semiloops in a spatially nonuniform magnetic field. Phys. Rev. E 101, 033306 (2020)

    Google Scholar 

  7. Gonçalves, W.C., Sardella, E., Becerra, V.F., et al.: Numerical solution of the time dependent Ginzburg–Landau equations for mixed (d+s) wave superconductors. J. Math. Phys. 55, 041501 (2014)

    MathSciNet  MATH  Google Scholar 

  8. Spirn, D.: Vortex dynamics of the full time-dependent Ginzburg–Landau equations. Commu. Pure Appl. Math. 55, 537–581 (2002)

    MathSciNet  MATH  Google Scholar 

  9. Gunter, D.O., Kaper, H.G., Leaf, G.K.: Implicit integration of the time-dependent Ginzburg–Landau equations of superconductivity. SIAM J. Sci. Comput. 23, 1943–1958 (2002)

    MathSciNet  MATH  Google Scholar 

  10. Jing, Z., Yong, H., Zhou, Y.: Thermal coupling effect on the vortex dynamics of superconducting thin films: time-dependent Ginzburg–Landau simulations. Supercond. Sci. Techn. 31, 055007 (2018)

    Google Scholar 

  11. Coskun, E., Kwong, M.K.: Simulating vortex motion in superconducting films with the time-dependent Ginzburg–Landau equations. Nonlinear 10, 579 (1997)

    MathSciNet  MATH  Google Scholar 

  12. Chapman, S.J., Howison, S.D., Ockendon, J.R.: Macroscopic models for superconductivity. SIAM Rev. 34, 529–560 (1992)

    MathSciNet  MATH  Google Scholar 

  13. Du, Q., Gunzburger, M.D., Peterson, J.S.: Analysis and approximation of the Ginzburg–Landau model of superconductivity. SIAM Rev. 34, 54–81 (1992)

    MathSciNet  MATH  Google Scholar 

  14. Du, Q.: Global existence and uniqueness of solutions of the time-dependent Ginzburg–Landau model for superconductivity. Appl. Anal. 53, 1–17 (1994)

    MathSciNet  MATH  Google Scholar 

  15. Nédélec, J.C.: Mixed finite elements in \(\Re ^3\). Numer. Math. 35, 315–341 (1980)

    MathSciNet  MATH  Google Scholar 

  16. Bangerth, W., Rannacher, R.: Adaptive Finite Element Methods for Differential Equations. Springer Basel AG, Basel (2003)

    MATH  Google Scholar 

  17. Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems I: a linear model problem. SIAM J. Numer. Anal. 28, 43–77 (1991)

    MathSciNet  MATH  Google Scholar 

  18. Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems IV: nonlinear problems. SIAM J. Numer. Anal. 32, 1729–1749 (1995)

    MathSciNet  MATH  Google Scholar 

  19. John, V., Linke, A., Merdon, C., Neilan, M., Rebholz, L.G.: On the divergence constraint in mixed finite element methods for incompressible flows. SIAM Rev. 59, 492–544 (2017)

    MathSciNet  MATH  Google Scholar 

  20. Leis, R.: Zur Theorie elektromagnetischer Schwingungen in anisotropen inhomogenen Medien. Math. Z. 106, 213–224 (1968)

    MathSciNet  Google Scholar 

  21. Duan, H.Y., Jia, F., Lin, P., Tan, R.C.E.: The local \(L^2\) projected \(C^0\) finite element method for Maxwell problem. SIAM J. Numer. Anal. 47, 1274–1303 (2009)

    MathSciNet  MATH  Google Scholar 

  22. Duan, H.Y., Lin, P., Saikrishnan, P., Tan, R.C.E.: A least squares finite element method for the magnetostatic problem in a multiply-connected Lipschitz domain. SIAM J. Numer. Anal. 45, 2537–2563 (2007)

    MathSciNet  MATH  Google Scholar 

  23. Costabel, M., Dauge, M.: Singularities of electromagnetic fields in polyhedral domains. Arch. Rational Mech. Anal. 151, 221–276 (2000)

    MathSciNet  MATH  Google Scholar 

  24. Girault, V., Raviart, P.-A.: Finite Element Methods for Navier–Stokes Equations. Springer, Berlin (1986)

    MATH  Google Scholar 

  25. Gao, H., Li, B., Sun, W.: Optimal error estimates of linearized Crank–Nicolson Galerkin FEMs for the time-dependent Ginzburg–Landau equations in superconductivity. SIAM J. Numer. Anal. 52, 1183–1202 (2014)

    MathSciNet  MATH  Google Scholar 

  26. Duan, H.Y., Lin, P., Tan, R.C.E.: \(C^0\) elements for generalized indefinite Maxwell’s equations. Numer. Math. 122, 61–99 (2012)

    MathSciNet  Google Scholar 

  27. Duan, H.Y., Tan, R.C.E., Yang, S.-Y., You, C.-S.: Computation of Maxwell singular solution by nodal-continuous elements. J. Comput. Phys. 268, 63–83 (2014)

    MathSciNet  MATH  Google Scholar 

  28. Duan, H.Y., Lin, P., Tan, R.C.E.: Analysis of a continuous finite element method for H(curl, div)-elliptic interface problem. Numer. Math. 123, 671–707 (2013)

    MathSciNet  MATH  Google Scholar 

  29. Duan, H.Y., Lin, P., Tan, R.C.E.: A finite element method for a Curlcurl-Graddiv eigenvalue interface problem. SIAM J. Numer. Anal. 54, 1193–1228 (2016)

    MathSciNet  MATH  Google Scholar 

  30. Gao, H., Sun, W.: An efficient fully linearized semi-implicit Galerkin-mixed FEM for the dynamical Ginzburg–Landau equations of superconductivity. J. Comput. Phys. 294, 329–345 (2015)

    MathSciNet  MATH  Google Scholar 

  31. Gao, H., Sun, W.: Analysis of linearized Galerkin-mixed FEMs for the time-dependent Ginzburg–Landau equations of superconductivity. Adv. Comput. Math. 44, 923–949 (2018)

    MathSciNet  MATH  Google Scholar 

  32. Gao, H.: Efficient numerical solution of dynamical Ginzburg–Landau equations under the Lorentz gauge. Commun. Comput. Phys. 22, 182–201 (2017)

    MathSciNet  MATH  Google Scholar 

  33. Yang, C.: Convergence of linearized backward Euler-Galerkin finite element methods for the time-dependent Ginzburg–Landau equations with temporal gauge. Int. J. Comput. Math. 91, 1507–1515 (2014)

    MathSciNet  MATH  Google Scholar 

  34. Yang, C.: A linearized Crank-Nicolson-Galerkin FEM form the time-dependent Ginzburg–Landau equations under the temporal gauge. Numer. Methods Part. Diff. Equ. 2014(30), 1279–1290 (2014)

    MATH  Google Scholar 

  35. Gao, H., Sun, W.: A new mixed formulation and efficient numerical solution of Ginzburg–Landau equations under the temporal gauge. SIAM J. Sci. Comput. 38, A1339–A1357 (2016)

    MathSciNet  MATH  Google Scholar 

  36. Wu, C., Sun, W.: Analysis of Galerkin FEMs for mixed formulation of time-dependent Ginzburg–Landau equations under temporal gauge. SIAM J. Numer. Anal. 56, 1291–1312 (2018)

    MathSciNet  MATH  Google Scholar 

  37. Gao, H., Ju, L., Xie, W.: A stabilized semi-implicit Euler Gauge-invariant method for the time-dependent Ginzburg–Landau equations. J. Sci. Comput. 80, 1083–1115 (2019)

    MathSciNet  MATH  Google Scholar 

  38. Adams, R.A.: Sobolev Spaces. Academic Press, New York (1975)

    MATH  Google Scholar 

  39. Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer, Berlin (2007)

    MATH  Google Scholar 

  40. Grisvard, P.: Boundary Value Problems in Non-Smooth Domains. Univ. of Maryland, Dept. of Math., Lecture Notes (19) (1980)

  41. Amrouche, C., Bernardi, C., Dauge, M., Girault, V.: Vector potentials in three-dimensional non-smooth domains. Math. Methods Appl. Sci. 21, 823–864 (1998)

    MathSciNet  MATH  Google Scholar 

  42. Ciarlet, P.G.: Basic error estimates for elliptic problems. In: Ciarlet, P.G., Lions, J.-L. (eds.) Handbook of Numerical Analysis, Vol. II, Finite Element Methods (Part 1). North-Holland, Amsterdam (1991)

    Google Scholar 

  43. Duan, H.Y., Qiu, F.J., Tan, R.C.E., Zheng, W.Y.: An adaptive FEM for a Maxwell interface problem. J. Sci. Comput. 67, 669–704 (2016)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for their very valuable comments and suggestions which have greatly helped the authors improve the presentation of the paper.

Funding

This work was supported by National Natural Science Foundation of China (11971366,11571266 and 11661161017) and by the Hubei Key Laboratory of Computational Science, Wuhan University, China (2019CFA007).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Wuhan University, Wuhan, 430072, China

    Huoyuan Duan & Qiuyu Zhang

Authors
  1. Huoyuan Duan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Qiuyu Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors contributed to the study conception and design. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Huoyuan Duan.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Duan, H., Zhang, Q. Residual-Based a Posteriori Error Estimates for the Time-Dependent Ginzburg–Landau Equations of Superconductivity. J Sci Comput 93, 79 (2022). https://doi.org/10.1007/s10915-022-02041-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-02041-0

Keywords

Mathematics Subject Classification