Skip to main content
SpringerLink
Log in

A Class of Efficient Hamiltonian Conservative Spectral Methods for Korteweg-de Vries Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

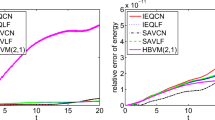
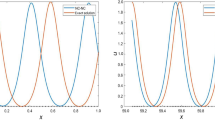
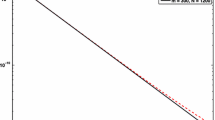
In this paper, we present and introduce two efficient Hamiltonian conservative fully discrete numerical schemes for Korteweg-de Vries equations. The new numerical schemes are constructed by using time-stepping spectral Petrov-Galerkin (SPG) or Gauss collocation (SGC) methods for the temporal discretization coupled with the p-version/spectral local discontinuous Galerkin (LDG) methods for the space discretization. We prove that the fully discrete SPG-LDG scheme preserves both the momentum and the Hamilton energy exactly for generalized KdV equations. While the fully discrete SGC-LDG formulation preserves the momentum and the Hamilton energy exactly for linearized KdV equations. As for nonlinear KdV equations, the SGC-LDG scheme preserves the momentum exactly and is Hamiltonian conserving up to some spectral accuracy. Furthermore, we show that the fully-discrete SGC-LDG and SPG-LDG methods converge exponentially with respect to the polynomial degree in both space and time for linear KdV equations. The numerical experiments are provided to demonstrate that the proposed numerical methods preserve the momentum, \(L^2\) energy and Hamilton energy and maintain the shape of the solution phase efficiently over long time period.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data Availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. An, J., Cao, W., Zhang, Z.: A class of efficient spectral methods and error analysis for nonlinear Hamiltonian systems. Commun. Math. Sci. 18(2), 395–428 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  2. Arnold, D.N., Winther, R.: A superconvergent finite element method for the Korteweg-de Vries equation. Math. Comput. 38, 23–36 (1982)

    Article  MATH  Google Scholar 

  3. Cao, W., Huang, Q.: Superconvergence of local discontinuous Galerkin methods for partial differential equations with higher order derivatives. J. Sci. Comput. 72, 761–791 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cheng, Y., Shu, C.-W.: A discontinuous Galerkin finite element method for time dependent partial differential equations with higher order derivatives. Math. Comput. 77, 699–730 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cui, Y., Mao, D.: Numerical method statisfying the first two conservation laws for the Korteweg-de Vries equation. J. Comput. Phys. 227(1), 376–399 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Davis, P.J., Rabinowitz, P.: Methods of numerical integration. Elsevier, Holland (1984)

    MATH  Google Scholar 

  7. Furihata, D.: Finite difference schemes for \(\frac{\partial u}{\partial t}=(\frac{\partial }{\partial x})^a \frac{\delta g}{\delta u}\) that inherit energy conservation or dissipation property. J. Comput. Phys. 156, 181–205 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  8. Goda, K.: Numerical studies on recurrence of the Korteweg-de Vries equation. J. Phys. Soc. Jpn. 42, 1040–1046 (1977)

    Article  Google Scholar 

  9. Greig, I.S., Morris, J.L.: A hopscotch method for the Korteweg-de Vries equation. J. Comput. Phys. 20, 64–80 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  10. Guo, B.-Y., Shen, J.: On spectral approximations using modified Legendre rational functions: application to the Korteweg-de Vries equation on the half line. Indiana Univ. Math. J. 50(1), 181–204 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  11. Guo, B.-Y., Wang, Q.-Z.: Legendre-Gauss collocation methods for ordinary differential equations. Adv. Comput. Math. 30, 249–280 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Huang, W., Sloan, D.M.: The pseudospectral method for third-order differential equations. SIAM J. Numer. Anal. 29, 1626–1647 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  13. Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 39(5), 422–443 (1895)

    Article  MathSciNet  MATH  Google Scholar 

  14. Liu, H., Yan, J.: A local discontinuous Galerkin method for the Korteweg-de Vries equation with boundary effect. J. Comput. Phys. 215, 197–218 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  15. Liu, H., Yi, N.: A Hamiltonian preserving discontinuous Galerkin method for the generalized Korteweg-de Vries equation. J. Comput. Phys. 321, 776–796 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  16. Ma, H., Sun, W.: A Legendre-Petrov-Galerkin and Chebyshev collocation method for third-order differential equations. SIAM J. Numer. Anal. 38, 1425–1438 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  17. Sanz-Serna, J.M., Christie, I.: Petrov-Galerkin methods for nonlinear dispersive wave. J. Comput. Phys. 39, 23–43 (1980)

    MathSciNet  Google Scholar 

  18. Shen, J.: A new dual-Petrov-Galerkin method for third and higher odd-order differential equations: application to the KdV equation. SIAM J. Numer. Anal. 41, 1595–1619 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Winther, R.: A conservative finite element method for the Korteweg-de Vries equation. Math. Comput. 34, 23–43 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  20. Xu, Y., Shu, C.-W.: Local discontinuous Galerkin methods for two classes of two-dimensional nonlinear wave equations. Phys. D 208, 21–58 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  21. Xu, Y., Shu, C.-W.: Error estimates of the semi-discrete local discontinuous Galerkin method for nonlinear convection-diffusion and kdv equations. Comput. Methods Appl. Mech. Eng. 196, 3805–3822 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. Yi, N., Huang, Y., Liu, H.: A direct discontinuous Galerkin method for the generalized Korteweg-de Vries equation: Energy conservation and boundary effect. J. Comput. Phys. 242(6), 351–366 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  23. Zabusky, N.J., Kruskal, M.D.: Interactions of ‘solitons’ in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243 (1965)

    Article  MATH  Google Scholar 

  24. Zhang, Q., Xia, Y.: Conservative and dissipative local discontinuous Galerkin methods for Korteweg-de Vries type equations. Commun. Comput. Phys. 25(2), 532–563 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhang, Z.: Superconvergent of spectral collocation and \(p\)-version methods in one dimensional problems. Math. Comput. 74(252), 1621–1636 (2005)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Beijing Normal University, Beijing, 100875, China

    Xu Yin & Waixiang Cao

Authors
  1. Xu Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Waixiang Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Waixiang Cao.

Ethics declarations

Conflict of interest

The author declares no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work is supported in part by the National Natural Science Foundation of China under Grants No. 11871106 and 12271049.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yin, X., Cao, W. A Class of Efficient Hamiltonian Conservative Spectral Methods for Korteweg-de Vries Equations. J Sci Comput 94, 10 (2023). https://doi.org/10.1007/s10915-022-02061-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-02061-w

Keywords

Mathematics Subject Classification

Search

Navigation