Abstract
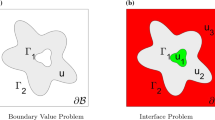
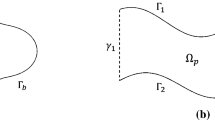
We develop a simple and efficient dimension splitting method for solving time dependent partial differential equations (PDEs) on multiple space dimensional irregular domains using a one dimensional kernel-free boundary integral (KFBI) method. The proposed method extends the alternating direction implicit methods and locally one dimensional methods to more general cases involving complex geometry. The KFBI method is a potential theory based Cartesian grid method, which works as an improvement of conventional boundary integral methods. In the KFBI method, boundary or volume integrals are evaluated by solving equivalent interface problems without using any analytic expression of Green’s functions. The one dimensional interface problems after dimension splitting are solved by finite difference method. The resulting linear systems are tri-diagonal and efficiently solved by the Thomas algorithm. The one dimensional kernel-free boundary integral method is rigorously proved to have second-order convergence rate in the maximum norm. Multiple numerical examples, including different types of PDEs and a free boundary problem, are presented to demonstrate the advantages of the proposed method. Numerical results show that the proposed method is efficient and achieves overall second order accuracy.






Similar content being viewed by others
Data availibility
The custom code of the current study is available at https://github.com/zhouhan-sjtu/KFBI-OS. The data generated in this study are available upon reasonable request.
References
Beale, J.T.: A grid-based boundary integral method for elliptic problems in three dimensions. SIAM J. Numer. Anal. 42(2), 599–620 (2004)
Chen, S., Merriman, B., Osher, S., Smereka, P.: A simple level set method for solving Stefan problems. J. Comput. Phys. 135(1), 8–29 (1997)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. SIAM (2002)
Douglas, J., Gunn, J.E.: Alternating direction methods for parabolic systems in mspace variables. J. ACM (JACM) 9(4), 450–456 (1962)
Douglas, J., Jr.: On the numerical integration of \(\frac{\partial ^2 u}{\partial x^2 } + \frac{\partial ^2 u}{\partial y^2 } = \frac{\partial u}{\partial t}\) by implicit methods. J. Soc. Ind. Appl. Math. 3(1), 42–65 (1955)
D’Yakonov, E.: Difference schemes with splitting operators for multidimensional unsteady problems (English translation). URSS Comp. Math. 3, 581–607 (1963)
Geiser, J.: Operator splitting methods for wave equations. Int. Math. Forum 2 (2007)
Hughes, T.J.R.: The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Courier Corporation (2012)
Hundsdorfer, W., Verwer, J.G.: Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations, vol. 33. Springer (2007)
Kim, S., Lim, H.: High-order schemes for acoustic waveform simulation. Appl. Numer. Math. 57(4), 402–414 (2007)
Kress, R.: Linear Integral Equations, vol. 82. Springer (1989)
LeVeque, R.J., Li, Z.: The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 31(4), 1019–1044 (1994)
Li, Z., Mayo, A.: ADI Methods for Heat Equations with Discontinuities Along an Arbitrary Interface. IBM Thomas J, Watson Research Division (1993)
Li, Z.: A fast iterative algorithm for elliptic interface problems. SIAM J. Numer. Anal. 35(1), 230–254 (1998)
Liu, J., Zheng, Z.: A dimension by dimension splitting immersed interface method for heat conduction equation with interfaces. J. Comput. Appl. Math. 261, 221–231 (2014)
Liu, J.K., Zheng, Z.S.: Efficient high-order immersed interface methods for heat equations with interfaces. Appl. Math. Mech. (Engl. Ed.) 35(9), 1189–1202 (2014)
Ma, C., Zhang, Q., Zheng, W.: A high-order fictitious-domain method for the advection-diffusion equation on time-varying domain. arXiv e-prints arXiv:2104.01870 (2021)
Mayo, A.: The fast solution of Poisson’s and the biharmonic equations on irregular regions. SIAM J. Numer. Anal. 21(2), 285–299 (1984)
Osher, S., Sethian, J.A.: Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 79(1), 12–49 (1988)
Peaceman, D.W., Rachford, H.H., Jr.: The numerical solution of parabolic and elliptic differential equations. J. Soc. Ind. Appl. Math. 3(1), 28–41 (1955)
Peskin, C.S.: The immersed boundary method. Acta Numerica 11, 479–517 (2002)
Saad, Y.: Iterative Methods for Sparse Linear Systems. SIAM (2003)
Strang, G.: On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 5(3), 506–517 (1968)
Wei, Z., Li, C., Zhao, S.: A spatially second order alternating direction implicit (adi) method for solving three dimensional parabolic interface problems. Comput. Math. Appl. 75(6), 2173–2192 (2018)
Xie, Y., Ying, W.: A fourth-order kernel-free boundary integral method for the modified Helmholtz equation. J. Sci. Comput. 78(3), 1632–1658 (2019)
Xie, Y., Ying, W.: A fourth-order kernel-free boundary integral method for implicitly defined surfaces in three space dimensions. J. Comput. Phys. 415, 109526 (2020)
Xie, Y., Ying, W.: A high-order kernel-free boundary integral method for incompressible flow equations in two space dimensions. Numer. Math. 13(3), 595–619 (2020)
Xie, Y., Ying, W., Wang, W.C.: A high-order kernel-free boundary integral method for the biharmonic equation on irregular domains. J. Sci. Comput. 80(3), 1681–1699 (2019)
Yanenko, N.N.: On the convergence of the splitting method for the heat conductivity equation with variable coefficients. USSR Comput. Math. Math. Phys. 2(5), 1094–1100 (1963)
Ying, W.: A cartesian grid-based boundary integral method for an elliptic interface problem on closely packed cells. Commun. Comput. Phys. 24(4), 1196–1220 (2018)
Ying, W., Henriquez, C.S.: A kernel-free boundary integral method for elliptic boundary value problems. J. Comput. Phys. 227(2), 1046–1074 (2007)
Ying, W., Wang, W.C.: A kernel-free boundary integral method for implicitly defined surfaces. J. Comput. Phys. 252, 606–624 (2013)
Ying, W., Wang, W.C.: A kernel-free boundary integral method for variable coefficients elliptic pdes. Commun. Comput. Phys. 15(4), 1108–1140 (2014)
Zhao, S.: A matched alternating direction implicit (adi) method for solving the heat equation with interfaces. J. Sci. Comput. 63(1), 118–137 (2015)
Zhou, H., Ying, W.: https://github.com/zhouhan-sjtu/KFBI-OS (2022)
Zhou, Y.C., Zhao, S., Feig, M., Wei, G.W.: High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources. J. Comput. Phys. 213(1), 1–30 (2006)
Zienkiewicz, O.C., Taylor, R.L., Zhu, J.Z.: The Finite Element Method: Its Basis and Fundamentals. Elsevier (2005)
Funding
This work is financially supported by the National Key R & D Program of China, Project Number 2020YFA0712000. It is also partially supported by the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA25010405), the National Natural Science Foundation of China (Grant No. DMS-11771290) and the Science Challenge Project of China (Grant No. TZ2016002).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work. There is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is financially supported by the National Key R &D Program of China, Project Number 2020YFA0712000. It is also partially supported by the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA25010405), the National Natural Science Foundation of China (Grant No. DMS-11771290) and the Science Challenge Project of China (Grant No. TZ2016002).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhou, H., Ying, W. A Dimension Splitting Method for Time Dependent PDEs on Irregular Domains. J Sci Comput 94, 20 (2023). https://doi.org/10.1007/s10915-022-02066-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-022-02066-5
Keywords
- Time dependent PDEs
- Time splitting method
- Cartesian grid
- ADI method
- LOD method
- Kernel-free boundary integral method