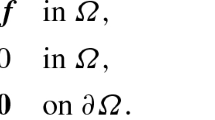Skip to main content
Springer Nature Link
Log in

Penalty-Free Any-Order Weak Galerkin FEMs for Linear Elasticity on Quadrilateral Meshes

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

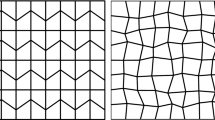
This paper develops a family of new weak Galerkin (WG) finite element methods (FEMs) for solving linear elasticity in the primal formulation. For a convex quadrilateral mesh, degree \( k \ge 0 \) vector-valued polynomials are used independently in element interiors and on edges for approximating the displacement. No penalty or stabilizer is needed for these new methods. The methods are free of Poisson-locking and have optimal order \( (k+1) \) convergence rates in displacement, stress, and dilation (divergence of displacement). Numerical experiments on popular test cases are presented to illustrate the theoretical estimates and demonstrate efficiency of these new solvers. Extension to cuboidal hexahedral meshes is briefly discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data Availability

The code used in this work will be made available upon request to the authors.

References

  1. Arbogast, T., Correa, M.R.: Two families of H(div) mixed finite elements on quadrilaterals of minimal dimension. SIAM J. Numer. Anal. 54, 3332–3356 (2016)

    MathSciNet  MATH  Google Scholar 

  2. Arbogast, T., Tao, Z.: Construction of H(div)-conforming mixed finite elements on cuboidal hexahedra. Numer. Math. 142, 1–32 (2019)

    MathSciNet  MATH  Google Scholar 

  3. Arnold, D.N., Awanou, G., Qiu, W.: Mixed finite elements for elasticity on quadrilateral meshes. Adv. Comput. Math. 41, 553–572 (2015)

    MathSciNet  MATH  Google Scholar 

  4. Artioli, E., Beirao da Veiga, L., Lovadina, C., Sacco, E.: Arbitrary order 2D virtual elements for polygonal meshes: part I, elastic problem. Comput. Mech. 60, 355–377 (2017)

    MathSciNet  MATH  Google Scholar 

  5. Artioli, E., Beirao da Veiga, L., Lovadina, C., Sacco, E.: Arbitrary order 2D virtual elements for polygonal meshes: part II, inelastic problem. Comput. Mech. 60, 643–657 (2017)

    MathSciNet  MATH  Google Scholar 

  6. Babuska, I., Suli, M.: The h-p version of the finite element method with quasiuniform meshes. Math. Model. Numer. Anal. 21, 199–238 (1987)

    MathSciNet  MATH  Google Scholar 

  7. Beirao da Veiga, L., Brezzi, F., Cangiani, A., Manzini, G., Marini, L.D., Russo, A.: Basic principles of virtual element methods. Math. Models Methods Appl. Sci. 23, 199–214 (2013)

    MathSciNet  MATH  Google Scholar 

  8. Beirao da Veiga, L., Brezzi, F., Marini, L.D.: Virtual elements for linear elasticity problems. SIAM J. Numer. Anal. 51(2), 794–812 (2013)

    MathSciNet  MATH  Google Scholar 

  9. Beirao da Veiga, L., Lovadina, C., Mora, D.: A virtual element method for elastic and inelastic problems on polytope meshes. Comput. Methods Appl. Mech. Eng. 295, 327–346 (2015)

    MathSciNet  MATH  Google Scholar 

  10. Berbatov, K.B., Lazarov, S., Jivkov, A.P.: A guide to the finite and virtual element methods for elasticity. Appl. Numer. Math. 169, 351–395 (2021)

    MathSciNet  MATH  Google Scholar 

  11. Bower, A.F.: Applied Mechanics of Solids. CRC Press, London (2010)

    Google Scholar 

  12. Brenner, S.: A nonconforming mixed multigrid method for the pure displacement problem in planar linear elasticity. SIAM J. Numer. Anal. 30, 116–135 (1993)

    MathSciNet  MATH  Google Scholar 

  13. Brenner, S., Scott, L.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 15, 3rd edn. Springer, New York (2008)

    MATH  Google Scholar 

  14. Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer, Berlin (1991)

    MATH  Google Scholar 

  15. Carstensen, C., Schedensack, M.: Medius analysis and comparison results for first-order finite element methods in linear elasticity. IMA J. Numer. Anal. 35, 1591–1621 (2015)

    MathSciNet  MATH  Google Scholar 

  16. Chen, G., Xie, X.: A robust weak Galerkin finite element method for linear elasticity with strong symmetric stresses. Comput. Methods Appl. Math. 16(3), 389–408 (2016)

    MathSciNet  MATH  Google Scholar 

  17. Chen, L., Huang, X.: A finite element elasticity complex in three dimensions. Math. Comput. 91, 2095–2127 (2022)

    MathSciNet  MATH  Google Scholar 

  18. Chen, L., Huang, X.: Finite elements for div- and divdiv-conforming symmetric tensors in arbitrary dimension. SIAM J. Numer. Anal. 60(4), 1932–1961 (2022)

    MathSciNet  MATH  Google Scholar 

  19. Chen, L., Wang, J., Ye, X.: A posteriori error estimates for weak Galerkin finite element methods for second order elliptic problems. J. Sci. Comput. 59, 496–511 (2014)

    MathSciNet  MATH  Google Scholar 

  20. Chou, S.-H., He, S.: On the regularity and uniformness conditions on quadrilateral grids. Comput. Meth. Appl. Mech. Eng. 191, 5149–5158 (2002)

    MathSciNet  MATH  Google Scholar 

  21. Falk, R.S.: Nonconforming finite element methods for the equations of linear elasticity. Math. Comput. 57(196), 529–550 (1991)

    MathSciNet  MATH  Google Scholar 

  22. Feng, Y., Liu, Y., Wang, R., Zhang, S.: A stabilizer-free weak Galerkin finite element method for the Stokes equations. Adv. Appl. Math. Mech. 14(1), 181–201 (2021)

    MathSciNet  MATH  Google Scholar 

  23. Fu, G., Cockburn, B., Stolarski, H.: Analysis of an HDG method for linear elasticity. Int. J. Numer. Methods Eng. 102(3–4), 551–575 (2015)

    MathSciNet  MATH  Google Scholar 

  24. Gain, A., Talischi, C., Paulino, G.: On the virtual element method for three-dimensional linear elasticity problems on arbitrary polyhedral meshes. Comput. Methods Appl. Mech. Eng. 282, 132–160 (2014)

    MathSciNet  MATH  Google Scholar 

  25. Harper, G., Liu, J., Tavener, S., Zheng, B.: Lowest-order weak Galerkin finite element methods for linear elasticity on rectangular and brick meshes. J. Sci. Comput. 78, 1917–1941 (2019)

    MathSciNet  MATH  Google Scholar 

  26. Hu, J.: A new family of efficient conforming mixed finite elements on both rectangular and cuboid meshes for linear elasticity in the symmetric formulation. SIAM J. Numer. Anal. 53(3), 1438–1463 (2015)

    MathSciNet  MATH  Google Scholar 

  27. Hu, J., Man, H., Wang, J., Zhang, S.: The simplest nonconforming mixed finite element method for linear elasticity in the symmetric formulation on n-rectangular grids. Comput. Math. Appl. 71(7), 1317–1336 (2016)

    MathSciNet  MATH  Google Scholar 

  28. Li, J., Ye, X., Zhang, S.: A weak Galerkin least-squares finite element method for div-curl systems. J. Comput. Phys. 363, 79–86 (2018)

    MathSciNet  MATH  Google Scholar 

  29. Liu, J., Cali, R.: A note on the approximation properties of the locally divergence-free finite elements. Int. J. Numer. Anal. Model. 5, 693–703 (2008)

    MathSciNet  MATH  Google Scholar 

  30. Liu, J., Sadre-Marandi, F., Wang, Z.: DarcyLite: a Matlab toolbox for Darcy flow computation. Procedia Comput. Sci. 80, 1301–1312 (2016)

    Google Scholar 

  31. Liu, J., Tavener, S., Wang, Z.: Lowest-order weak Galerkin finite element method for Darcy flow on convex polygonal meshes. SIAM J. Sci. Comput. 40(5), B1229–B1252 (2018)

    MathSciNet  MATH  Google Scholar 

  32. Liu, J., Tavener, S., Wang, Z.: Penalty-free any-order weak Galerkin FEMs for elliptic problems on quadrilateral meshes. J. Sci. Comput. 83(3), 1–19 (2020)

    MathSciNet  MATH  Google Scholar 

  33. Nguyen, N.C., Peraire, J., Cockburn, B.: High-order implicit hybridizable discontinuous Galerkin methods for acoustics and elastodynamics. J. Comput. Phys. 230(10), 885 (2011)

    MathSciNet  MATH  Google Scholar 

  34. Qiu, W., Shen, J., Shi, K.: An HDG method for linear elasticity with strong symmetric stresses. Math. Comput. 87(309), 69–93 (2018)

    MathSciNet  MATH  Google Scholar 

  35. Soon, S.-C., Cockburn, B., Stolarski, H.K.: A hybridizable discontinuous Galerkin method for linear elasticity. Int. J. Numer. Methods Eng. 80(8), 1058–1092 (2009)

    MathSciNet  MATH  Google Scholar 

  36. Timoshenko, S.P., Goodier, J.N.: Theory of Elasticity. McGraw-Hill, New York (1970)

    MATH  Google Scholar 

  37. Wang, C.: New discretization schemes for time-harmonic Maxwell equations by weak Galerkin finite element methods. J. Comput. Appl. Math. 341, 127–143 (2018)

    MathSciNet  MATH  Google Scholar 

  38. Wang, C., Wang, J., Wang, R., Zhang, R.: A locking-free weak Galerkin finite element method for elasticity problems in the primal formulation. J. Comput. Appl. Math. 307, 346–366 (2016)

    MathSciNet  MATH  Google Scholar 

  39. Wang, J., Wang, R., Zhai, Q., Zhang, R.: A systematic study on weak Galerkin finite element methods for second order elliptic problems. J. Sci. Comput. 74(3), 1369–1396 (2018)

    MathSciNet  MATH  Google Scholar 

  40. Wang, J., Ye, X.: A weak Galerkin finite element method for second order elliptic problems. J. Comput. Appl. Math. 241, 103–115 (2013)

    MathSciNet  MATH  Google Scholar 

  41. Wang, J., Ye, X.: A weak Galerkin mixed finite element method for second-order elliptic problems. Math. Comput. 83, 2101–2126 (2014)

    MathSciNet  MATH  Google Scholar 

  42. Wang, J., Zhai, Q., Zhang, R., Zhang, S.: A weak Galerkin finite element scheme for the Cahn-Hilliard equation. Math. Comput. 88, 211–235 (2019)

    MathSciNet  MATH  Google Scholar 

  43. Wang, R., Zhang, R.: A weak Galerkin finite element method for the linear elasticity problem in mixed form. J. Comput. Math. 36, 469–491 (2018)

    MathSciNet  MATH  Google Scholar 

  44. Wang, Z., Tavener, S., Liu, J.: Analysis of a 2-field finite element solver for poroelasticity on quadrilateral meshes. J. Comput. Appl. Math. 393, 113539 (2021)

    MathSciNet  MATH  Google Scholar 

  45. Wang, Z., Wang, R., Liu, J.: Robust weak Galerkin finite element solvers for Stokes flow based on a lifting operator. Comput. Math. Appl. 125, 90–100 (2022)

    MathSciNet  MATH  Google Scholar 

  46. Yi, S.-Y.: A lowest-order weak Galerkin method for linear elasticity. J. Comput. Appl. Math. 350, 286–298 (2019)

    MathSciNet  MATH  Google Scholar 

  47. Zhang, Y., Wang, S., Chan, D.: A new five-node locking-free quadrilateral element based on smoothed FEM for near-incompressible linear elasticity. Int. J. Numer. Meth. Eng. 100, 633–668 (2014)

    MathSciNet  MATH  Google Scholar 

Download references

Funding

J. Liu was supported in part by US National Science Foundation under grant DMS-2208590. R. Wang was partially supported by the National Natural Science Foundation of China (grant No. 12001230, 11971198), the National Key Research and Development Program of China (grant No. 2020YFA0713602), and the Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education of China housed at Jilin University. Z. Wang was partially supported by the National Natural Science Foundation of China (grant No.12101626).

Author information

Authors and Affiliations

  1. School of Mathematics, Jilin University, Changchun, 130012, Jilin, China

    Ruishu Wang

  2. School of Mathematics (Zhuhai), Sun Yat-sen University, Zhuhai, 519082, Guangdong, China

    Zhuoran Wang

  3. Department of Mathematics, Colorado State University, Fort Collins, CO, 80523-1874, USA

    Jiangguo Liu

Authors
  1. Ruishu Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhuoran Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jiangguo Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhuoran Wang.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, R., Wang, Z. & Liu, J. Penalty-Free Any-Order Weak Galerkin FEMs for Linear Elasticity on Quadrilateral Meshes. J Sci Comput 95, 20 (2023). https://doi.org/10.1007/s10915-023-02151-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02151-3

Keywords

Mathematics Subject Classification