Abstract
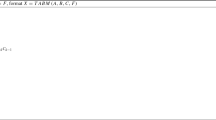
For differential equations with multiple order spatial derivatives, there are some shortcomings by the classical high order compact (HOC) discretization. At least one of them is reducing the computational efficiency due to the multiple inverse manipulation of matrices. This motivates us to design a new kind of compact method what is called combined high order compact methods. The basic idea lying in this kind of method is to solve all the spatial derivatives simultaneously. Then, it is used to solve coupled nonlinear Schrödinger (CNLS) equations which contain both the first and second order derivatives. This scheme is not only more compact and accurate than standard HOC scheme and standard finite difference method with the same order, but also it can construct structure-preserving schemes. It preserves the symplectic structure and mass, and sometimes energy and momentum. Numerical experiments indicate that the new scheme can simulate the CNLS equations very accurately and efficiently. The mass and momentum are exactly preserved. The energy is preserved in some especially cases.






Similar content being viewed by others
Data Availability
Enquiries about data availability should be directed to the authors.
References
Adam, Y.: A Hermitian finite difference method for the solution of parabolic equations. Comput. Math. Appl. 1, 393–406 (1975)
Bandrauk, A., Shen, H.: Exponential split operator methods for solving coupled time-dependent Schrödinger equations. J. Chem. Phys. 99, 1185–1193 (1993)
Bhatt, A., Floyd, D., Moore, B.: Second order conformal symplectic schemes for damped Hamiltonian systems. J. Sci. Comput. 66, 1234–1259 (2016)
Cano, B.: Conserved quantities of some Hamiltonian wave equation after full discretization. Numer. Math. 103, 197–223 (2006)
Chu, P., Fan, C.: A three-point combined compact difference scheme. J. Comput. Phys. 140, 370–399 (1998)
Chu, P., Fan, C.: A three-point sixth-order nonuniform combined compact difference scheme. J. Comput. Phys. 148, 663–674 (1999)
Chen, B., He, D., Pan, K.: A linearized high-order combined compact difference scheme for multi-dimensional coupled Burgers equations. Numer. Math. Theor. Methods Appl. 11, 299–320 (2018)
Chen, Y., Zhu, H., Song, S.: Multi-symplectic splitting method for the coupled nonlinear Schrödinger equation. Comput. Phys. Commun. 181, 1231–1241 (2010)
Feng, K., Qin, M.: Symplectic Geometric Algorithms for Hamiltonian Systems. Springer, Berlin (2010)
Goedheer, W., Potters, J.: A compact finite difference scheme on a non-equidistant mesh. J. Comput. Phys. 61, 269–279 (1985)
He, D., Pan, K.: An unconditionally stable linearized CCD-ADI method for generalized nonlinear Schrödinger equations with variable coefficients in two and three dimensions. Comput. Math. Appl. 73, 2360–2374 (2017)
He, Z., Kong, L., Fu, F.: The splitting high-order compact difference scheme for two-dimensional Gross-Pitaevskii equation. J. Jiangxi Norm. Univ. (Nat. Ed.) 44, 599–603 (2020)
Hao, Z., Sun, Z., Cao, W.: A three-level linearized compact difference scheme for the Ginzburg-Landau equation. Numer. Methods Part. Differ. Equ. 31, 876–899 (2015)
Hirsh, R.: Higher order accurate difference solutions of fluid mechanics problems by a compact differencing technique. J. Comput. Phys. 19, 90–109 (1975)
Ismail, M., Alamri, S.: Highly accurate finite difference method for coupled nonlinear Schrödinger equation. Inter. J. Comput. Math. 81, 333–351 (2004)
Kong, L., Zhu, P., Wang, Y., Zeng, Z.: Efficient and accurate numerical methods for the multidimensional convection-diffusion equations. Math. Comput. Simul. 162, 179–194 (2019)
Kong, L., Chen, M., Yin, X.: A novel kind of efficient symplectic scheme for Klein-Gordon-Schrödinger equation. Appl. Numer. Math. 135, 481–496 (2019)
Lele, S.K.: Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42 (1992)
Luo, Y., Wang, L., Wan, L., Kong, L.: The conformal splitting high-order compact difference scheme for damped nonlinear Schrödinger equation. J. Jiangxi Norm. Univ. (Nat. Ed.) 46, 210–214 (2022)
Ma, Y., Kong, L., Hong, J.: High-order compact splitting multisymplectic method for the coupled nonlinear Schrödinger equations. Comput. Math. Appl. 61, 319–333 (2011)
Shen, J., Xu, J., Yang, J.: A new class of efficient and robust energy stable schemes for gradient flows. SIAM Rev. 61, 474–506 (2019)
Sengupt, T., Vijay, V., Bhaumik, S.: Further improvement and analysis of CCD scheme: dissipation discretization and de-aliasing properties. J. Comput. Phys. 228, 6150–6168 (2009)
Wang, Y., Li, S.: New schemes for the coupled nonlinear Schrödinger equation. Inter. J. Comput. Math. 87, 775–787 (2010)
Wang, L., Cai, W., Wang, Y.: An energy-preserving scheme for the coupled Gross-Pitaevskii equations. Adv. Appl. Math. Mech. 13, 203–231 (2021)
Zhang, F., An, X.: A conservative finite difference scheme for nonlinear Schrödinger equation invllving quintic terms. Math. Numer. Sin. 44, 63–70 (2022)
Zhang, S.: Meshless symplectic and multi-symplectic local RBF collocation methods for Hamiltonian PDEs. J. Sci. Comput. 88, 90 (2021)
Funding
This work was supported by the NNSFC (Nos. 11961036, 12201263, 11972121), the Jiangxi Provincial Natural Science Foundation (Nos. 20224ACB201001, 20224ACB218001), the Natural Foundation from the Educational Department of Jiangxi Province (Nos. GJJ200310), the Growing Project for Young Science and Technology Talents of Educational Department of Guizhou Province (No. KY[2022]317), the Fundamental Research Project for Natural Science of Guizhou Province (No. ZK[2022]218)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, L., Kong, L., Chen, M. et al. Structure-Preserving Combined High-Order Compact Schemes for Multiple Order Spatial Derivatives Differential Equations. J Sci Comput 96, 8 (2023). https://doi.org/10.1007/s10915-023-02219-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02219-0
Keywords
- Combined high order compact schemes
- Computational efficiency
- Coupled nonlinear Schrödinger equations
- Conservation laws
- Structure-preserving scheme