Skip to main content
Springer Nature Link
Log in

Convergence Analysis of the Fully Discrete Projection Method for Inductionless Magnetohydrodynamics System Based on Charge Conservation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

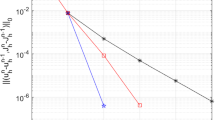
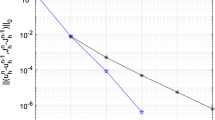
In this paper, we focus on a finite element projection method for inductionless magnetohydrodynamics equations. A fully discrete projection method based on Euler semi-implicit scheme is proposed in which continuous elements are used to approximate the Navier–Stokes equations and the divergence-conforming element is used to approximate the current density. The key of the projection method is that it must be compatible with two different spaces for calculating velocity, which leads to solve the pressure by solving a Poisson equation. The results show that the proposed projection scheme meets a discrete energy stability and the discrete current density keeps charge conservation property. In addition, this paper provides a rigorous optimal error analysis of velocity, pressure and current density. Finally, several numerical examples are performed to demonstrate both accuracy and efficiency of our proposed scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability

Enquiries about data availability should be directed to the authors.

References

  1. Abdou, M., Sze, D., Wong, C., Sawan, M., Ying, A., Morley, N., Malang, S.: U.S. plans and strategy for ITER blanket testing. Fusion Sci. Technol. 47, 475–487 (2005)

    Article  Google Scholar 

  2. Abdou, M., Ying, A., Morley, N., Gulec, K., Smolentsev, S., Kotschenreuther, M., Malang, S., Zinkle, S., Rognlien, T., Fogarty, P., et al.: On the exploration of innovative concepts for fusion chamber technology. Fusion Eng. Des. 2, 181–247 (2001)

    Article  Google Scholar 

  3. Achdou, Y., Guermond, J.-L.: Convergence analysis of a finite element projection/lagrange–Galerkin method for the incompressible Navier–Stokes equations. SIAM J. Numer. Anal. 37, 799–826 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  4. An, R., Li, Y.: Error analysis of first-order projection method for time-dependent magnetohydrodynamics equations. Appl. Numer. Math. 112, 167–181 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bell, J.B., Colella, P., Glaz, H.M.: A second-order projection method for the incompressible Navier–Stokes equations. J. Comput. Phys. 85, 257–283 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  6. Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications, vol. 44 of Springer Series in Computational Mathematics. Springer, Heidelberg (2013)

    Book  MATH  Google Scholar 

  7. Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods, vol. 15 of Springer Series in Computational Mathematics. Springer, New York (1991)

    Book  MATH  Google Scholar 

  8. Choi, H., Shen, J.: Efficient splitting schemes for magneto-hydrodynamic equations. Sci. China Math. 59, 1495–1510 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chorin, A.J.: Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 745–762 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chorin, A.J.: On the convergence of discrete approximations to the Navier–Stokes equations. Math. Comput. 23, 341–353 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  11. Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. Studies in Mathematics and Its Applications, vol. 4. North-Holland Publishing Co., Amsterdam (1978)

    Google Scholar 

  12. Davidson, P.A.: An Introduction to Magnetohydrodynamics. Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge (2001)

    Book  Google Scholar 

  13. de Frutos, J., García-Archilla, B., Novo, J.: Fully discrete approximations to the time-dependent Navier–Stokes equations with a projection method in time and grad-div stabilization. J. Sci. Comput. 80, 1330–1368 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  14. Ding, Q., He, X., Long, X., Mao, S.: Error analysis of a fully discrete projection method for magnetohydrodynamic system. Numer. Methods Partial Differ. Equ. 39, 1449–1477 (2023)

    Article  MathSciNet  Google Scholar 

  15. Gerbeau, J.-F., Le Bris, C., Lelièvre, T.: Mathematical Methods for the Magnetohydrodynamics of Liquid Metals. Numerical Mathematics and Scientific Computation. Oxford University Press, Oxford (2006)

    MATH  Google Scholar 

  16. Gresho, P.M.: On the theory of semi-implicit projection methods for viscous incompressible flow and its implementation via a finite element method that also introduces a nearly consistent mass matrix. I. Theory. Int. J. Numer. Methods Fluids 11, 587–620 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  17. Guermond, J.-L.: Some implementations of projection methods for Navier–Stokes equations. RAIRO Modél. Math. Anal. Numér. 30, 637–667 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  18. Guermond, J.-L., Quartapelle, L.: On the approximation of the unsteady Navier–Stokes equations by finite element projection methods. Numer. Math. 80, 207–238 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  19. Guermond, J.L., Shen, J.: On the error estimates for the rotational pressure-correction projection methods. Math. Comput. 73, 1719–1737 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  20. Guermond, J.L., Shen, J., Yang, X.: Error analysis of fully discrete velocity-correction methods for incompressible flows. Math. Comput. 77, 1387–1405 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. He, Y.: Unconditional convergence of the Euler semi-implicit scheme for the three-dimensional incompressible MHD equations. IMA J. Numer. Anal. 35, 767–801 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Heywood, J.G., Rannacher, R.: Finite-element approximation of the nonstationary Navier–Stokes problem. IV. Error analysis for second-order time discretization. SIAM J. Numer. Anal. 27, 353–384 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  23. Hiptmair, R.: Finite elements in computational electromagnetism. Acta Numer. 11, 237–339 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  24. Li, L., Ni, M.-J., Zheng, W.: A charge-conservative finite element method for inductionless MHD equations. Part I: convergence. SIAM J. Sci. Comput. (2019, to appear)

  25. Li, L., Ni, M.-J., Zheng, W.: A charge-conservative finite element method for inductionless MHD equations. Part II: a robust solver. SIAM J. Sci. Comput. (2019, to appear)

  26. Long, X., Ding, Q., Mao, S.: Error analysis of a conservative finite element scheme for time-dependent inductionless MHD problem. J. Comput. Appl. Math. 419, 114728 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  27. Moreau, R.: Magnetohydrodynamics, vol. 3 of Fluid Mechanics and Its Applications. Kluwer Academic Publishers Group, Dordrecht (1990). Translated from the French by A. F. Wright

  28. Ni, M.-J., Li, J.-F.: A consistent and conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part III: on a staggered mesh. J. Comput. Phys. 231, 281–298 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ni, M.-J., Munipalli, R., Huang, P., Morley, N.B., Abdou, M.A.: A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. II. On an arbitrary collocated mesh. J. Comput. Phys. 227, 205–228 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  30. Ni, M.-J., Munipalli, R., Morley, N.B., Huang, P., Abdou, M.A.: A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. I. On a rectangular collocated grid system. J. Comput. Phys. 227, 174–204 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  31. Planas, R., Badia, S., Codina, R.: Approximation of the inductionless MHD problem using a stabilized finite element method. J. Comput. Phys. 230, 2977–2996 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  32. Prohl, A.: On pressure approximation via projection methods for nonstationary incompressible Navier–Stokes equations. SIAM J. Numer. Anal. 47, 158–180 (2008/09)

  33. Rannacher, R.: On Chorin’s projection method for the incompressible Navier–Stokes equations. In: The Navier–Stokes Equations II—Theory and Numerical Methods (Oberwolfach, 1991), vol. 1530 of Lecture Notes in Mathematics, pp. 167–183. Springer, Berlin (1992)

  34. Shen, J.: Remarks on the pressure error estimates for the projection methods. Numer. Math. 67, 513–520 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  35. Shen, J.: On error estimates of the projection methods for the Navier–Stokes equations: second-order schemes. Math. Comput. 65, 1039–1065 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  36. Shen, J., Yang, X.: Error estimates for finite element approximations of consistent splitting schemes for incompressible flows. Discrete Contin. Dyn. Syst. Ser. B 8, 663–676 (2007)

    MathSciNet  MATH  Google Scholar 

  37. Weinan, E., Liu, J.-G.: Projection method. I. Convergence and numerical boundary layers. SIAM J. Numer. Anal. 32, 1017–1057 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  38. Yang, Y., Si, Z.: A consistent projection finite element method for the incompressible MHD equations. Appl. Anal. 100, 2606–2626 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  39. Zhang, L., Cui, T., Liu, H.: A set of symmetric quadrature rules on triangles and tetrahedra. J. Comput. Math. 27, 89–96 (2009)

    MathSciNet  MATH  Google Scholar 

  40. Zhang, L.-B.: A parallel algorithm for adaptive local refinement of tetrahedral meshes using bisection. Numer. Math. Theory Methods Appl. 2, 65–89 (2009)

    MathSciNet  MATH  Google Scholar 

Download references

Funding

This work is supported by the Natural Science Foundation of China (12201353), Program for IRTSTHN (22IRTSTHN013), Shandong Province Natural Science Foundation (ZR2021QA054) and the Talent Fund of Beijing Jiaotong University (2023XKRC024).

Author information

Authors and Affiliations

  1. College of Mathematics and Information Science, Henan University of Economics and Law, Zhengzhou, 450045, China

    Xiaonian Long

  2. School of Mathematics and Statistics, Beijing Jiaotong University, Beijing, 100044, China

    Qianqian Ding

Authors
  1. Xiaonian Long
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Qianqian Ding
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qianqian Ding.

Ethics declarations

Competing interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Long, X., Ding, Q. Convergence Analysis of the Fully Discrete Projection Method for Inductionless Magnetohydrodynamics System Based on Charge Conservation. J Sci Comput 96, 2 (2023). https://doi.org/10.1007/s10915-023-02226-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02226-1

Keywords