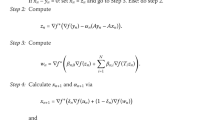Skip to main content
SpringerLink
Log in

Convergence Analysis of a New Bregman Extragradient Method for Solving Fixed Point Problems and Variational Inequality Problems in Reflexive Banach Spaces

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

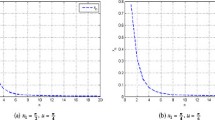
We mainly introduce a new self-adaptive extragradient method by using the inertial technique for solving variational inequality problems of pseudomonotone operators and fixed point problems of Bregman relatively nonexpansive mappings in real reflexive Banach spaces. Precisely, we show that the sequence generated by our iterative process converges strongly to a common element for the solution set of variational inequality problems and the set of fixed points of Bregman relatively nonexpansive mappings. Additionally, some numerical examples are given to show the effectiveness of our algorithm. The results obtained in this paper are the improvement and supplement of many recent ones in the field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data Availibility

My manuscript has no associated data.

References

  1. Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)

    MATH  Google Scholar 

  2. Iusem, A.N., Nasri, M.: Korpelevich method for variational inequality problems in Banach spaces. J. Glob. Optim. 50, 59–76 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  3. Kraikaew, R., Saejung, S.: Strong convergence of the Halpern subgradient extragradient method for solving variational inequalities in Hilbert spaces. J. Optim. Theory Appl. 163, 399–412 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Malitsky, Y.V.: Projected reflected gradient methods for monotone variational inequalities. SIAM J. Optim. 25, 502–520 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  5. Korpelevich, G.M.: The extragradient method for finding saddle points and other problems. Ekonom. i Mat. Metody. 12, 747–756 (1976)

    MathSciNet  MATH  Google Scholar 

  6. Censor, Y., Gibali, A., Reich, S.: The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 148, 318–335 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Thong, D.V., Triet, N.A., Li, X.H., Dong, Q.L.: Strong convergence of extragradient methods for solving bilevel pseudo-monotone variational inequality problems. Numer. Algorithms 83, 1123–1143 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  8. Shehu, Y., Gibali, A., Sagratella, S.: Inertial projection-type methods for solving quasi-variational inequalities in real Hilbert spaces. J. Optim. Theory Appl. 184, 877–894 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  9. Shehu, Y., Liu, L.L., Mu, X.W., Dong, Q.-L.: Analysis of versions of relaxed inertial projection and contraction method. Appl. Numer. Math. 165, 1–21 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  10. Shehu, Y., Iyiola, O.S., Thong, D.V., Van, N.T.C.: An inertial subgradient extragradient algorithm extended to pseudomonotone equilibrium problems. Math. Methods Oper. Res. 93, 213–242 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  11. Gibali, A., Thong, D.V., Tuan, P.A.: Two simple projection-type methods for solving variational inequalities. Anal. Math. Phys. 9, 2203–2225 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gibali, A., Thong, D.V.: A new low-cost double projection method for solving variational inequalities. Optim. Eng. 21, 1613–1634 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  13. Tang, Y., Gibali, A.: New self-adaptive step size algorithms for solving split variational inclusion problems and its applications. Numer. Algorithms 83, 305–331 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  14. Jolaoso, L.O., Shehu, Y.: Single Bregman projection method for solving variational inequalities in reflexive Banach spaces. Appl. Anal. 101, 4807–4828 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  15. Jolaoso, L.O., Aphane, M.: Bregman subgradient extrageadient method with monotone sele-adjustment stepsize for solving pseudomonotone variational inequalities and fixed point problems. J. Ind. Manag. Optim. 18, 773–794 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  16. Cai, G., Gibali, A., Iyiola, O.S., Shehu, Y.: A new double-projection method for solving variational inequalities in Banach spaces. J. Optim. Theory Appl. 178, 219–239 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  17. Shehu, Y.: Single projection algorithm for variational inequalities in Banach spaces with application to contact problem. Acta Math. Sci. Ser. B 40, 1045–1063 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  18. Hu, S., Wang, Y., Jing, P., Dong, Q.-L.: A new Bregman projection method with a self-adaptive process for solving variational inequality problem in reflexive Banach spaces. Optim. Lett. 17, 935–954 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  19. Reem, D., Reich, S., De Pierro, A.: Re-examination of Bregman functions and new properties of their divergences. Optimization 68, 279–348 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  20. Reem, D., Reich, S., De Pierro, A.: A telescopic Bregmanian proximal gradient method without the global Lipschitz continuity assumption. J. Optim. Theory Appl. 182, 851–884 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  21. Xie, Z.B., Cai, G., Dong, Q.-L.: Strong convergence of Bregman projection method for solving variational inequality problems in reflexive Banach spaces. Numer. Algorithms 93, 269–294 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  22. Hieu, D.V., Reich, S.: Two Bregman projection methods for solving variational inequalities. Optimization 71, 1777–1802 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  23. Jolaoso, L.O.: The subgradient extragradient method for solving pseudomonotone equilibrium and fixed point problems in Banach spaces. Optimization 71, 4051–4081 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  24. Taiwo, A., Jolaoso, L.O., Mewomo, O.T.: Inertial-type algorithm for solving split common fixed point problems in Banach spaces. J. Sci. Comput. 86(1), Paper No. 12, 30 pp (2021)

  25. Bauschke, H.H., Borwein, J.M., Combettes, P.L.: Essential smoothness, essential strict convexity, and Legendre functions in Banach spaces. Commun. Contemp. Math. 3, 615–647 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  26. Phelps, R.R.: Convex Functions, Monotone Operators, and Differentiability, second ed., in: Lecture Notes in Mathematics, vol, 1364. Springer, Berlin (1993)

  27. Bauschke, H.H., Borwein, J.M.: Legendre functions and the method of random Bregman projections. J. Convex Anal. 4, 27–67 (1997)

    MathSciNet  MATH  Google Scholar 

  28. Butnariu, D., Iusem, A.N.: Totally convex functions for fixed points computation and infinite dimensional optimization. Applied Optimization, 40. Kluwer Academic Publishers, Dordrecht (2000)

  29. Reich, S., Sabach, S.: A strong convergence theorem for a proximal-type algorithm in reflexive Banach spaces. J. Nonlinear Convex Anal. 10, 471–485 (2009)

    MathSciNet  MATH  Google Scholar 

  30. Martín-Márquez, V., Reich, S., Sabach, S.: Bregman strongly nonexpansive operators in reflexive Banach spaces. J. Math. Anal. Appl. 400, 597–614 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  31. Censor, Y., Lent, A.: An iterative row-action method for interval convex programming. J. Optim. Theory Appl. 34, 321–353 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  32. Naraghirad, E., Yao, J.-C.: Bregman weak ralatively nonexpansive mapping in Banach spaces. Fixed Point Theory Appl., 141, 43pp (2013)

  33. Reich, S., Tuyen, T.: Projection algorithms for solving the split feasibility problem with multiple output sets. J. Optimiz. Theory Appl. 190, 861–878 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  34. Maingé, P.E.: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 16, 899–912 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  35. Xu, H.K.: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 66, 240–256 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  36. Thong, D.V., Vuong, P.T.: Modified Tseng’s extragradient methods for solving pseudo-monotone variational inequalities. Optimization 68(11), 2207–2226 (2019)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was supported by the NSF of China (Grant No. 12171435).

Author information

Authors and Affiliations

  1. School of Marxism, Chongqing Normal University, Chongqing, Chongqing, 401331, China

    Shaotao Hu

  2. Department of Mathematics, Zhejiang Normal University, Jinhua, Zhejiang, 321004, China

    Shaotao Hu & Yuanheng Wang

  3. College of Science, Civil Aviation University of China, Tianjin, 300300, China

    Qiao-Li Dong

Authors
  1. Shaotao Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuanheng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qiao-Li Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The first draft of the manuscript was written by Shaotao Hu and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Yuanheng Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, S., Wang, Y. & Dong, QL. Convergence Analysis of a New Bregman Extragradient Method for Solving Fixed Point Problems and Variational Inequality Problems in Reflexive Banach Spaces. J Sci Comput 96, 19 (2023). https://doi.org/10.1007/s10915-023-02243-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02243-0

Keywords

Mathematics Subject Classification

Search

Navigation