Skip to main content
Springer Nature Link
Log in

Fast and Accuracy-Preserving Domain Decomposition Methods for Reduced Fracture Models with Nonconforming Time Grids

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

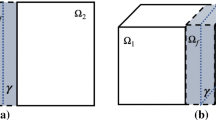
This paper is concerned with the numerical solution of compressible fluid flow in a fractured porous medium. The fracture represents a fast pathway (i.e., with high permeability) and is modeled as a hypersurface embedded in the porous medium. We aim to develop fast-convergent and accurate global-in-time domain decomposition (DD) methods for such a reduced fracture model, in which smaller time step sizes in the fracture can be coupled with larger time step sizes in the subdomains. Using the pressure continuity equation and the tangential PDEs in the fracture-interface as transmission conditions, three different DD formulations are derived; each method leads to a space-time interface problem which is solved iteratively and globally in time. Efficient preconditioners are designed to accelerate the convergence of the iterative methods while preserving the accuracy in time with nonconforming grids. Numerical results for two-dimensional problems with non-immersed and partially immersed fractures are presented to show the improved performance of the proposed methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

Enquiries about data availability should be directed to the authors.

References

  1. Alboin, C., Jaffré, J., Roberts, J.E., Serres, C.: Domain decomposition for flow in fractured porous media. In: Lai, C.H., Bjorstad, P.E., Cross, M., Widlund, O.B. (eds.) Domain Decomposition Methods in Science and Engineering, pp. 365–373. Domain Decomposition Press, Bergen (1999)

    Google Scholar 

  2. Alboin, C., Jaffre, J., Roberts, J.E., Serres, C.: Modeling fractures as interfaces for flow and transport in porous media. In: Fluid Flow and Transport in Porous Media: Mathematical and Numerical Treatment (South Hadley, MA), vol. 295 of Contemp. Math. Amer. Math. Soc. Providence, RI, vol. 2002, pp. 13–24 (2001)

  3. Amir, L., Kern, M., Martin, V., Roberts, J.E.: Décompositionn de domaine pour un milieu poreux fractureé: Un moèle en 3D avec fractures qui s’intersectent. Arima 5, 11–25 (2006)

    Google Scholar 

  4. Amir, L., Kern, M., Mghazli, Z., Roberts, J.E.: Intersecting fractures in porous media: mathematical and numerical analysis. Appl. Anal. (2021). https://doi.org/10.1080/00036811.2021.1981878

    Article  Google Scholar 

  5. Angot, P., Boyer, F., Hubert, F.: Asymptotic and numerical modelling of flows in fractured porous media. M2AN Math. Model. Numer. Anal. 43(2), 239–275 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bennequin, D., Gander, M.J., Gouarin, L., Halpern, L.: A homographic best approximation problem with application to optimized Schwarz waveform relaxation. Math. Comput. 78(265), 185–223 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Blayo, E., Debreu, L., Lemarié, F.: Toward an optimized global-in-time Schwarz algorithm for diffusion equation with discontinuous and spatially variable coefficients. Part 1: the constant coefficients case. Electron. Trans. Numer. Anal. 40, 170–186 (2013)

    MathSciNet  MATH  Google Scholar 

  8. Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Elements Methods and Applications. Springer, Heidelberg (2013)

    Book  MATH  Google Scholar 

  9. Brunner, F., Radu, F.A., Knabner, P.: Analysis of an upwind-mixed hybrid finite element method for transport problems. SIAM J. Numer. Anal. 52, 83–102 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cowsar, L.C., Mandel, J., Wheeler, M.F.: Balancing domain decomposition for mixed finite elements. Math. Comput. 64, 989–1015 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  11. Farhat, C., Chen, P.S., Mandel, J.: A scalable Lagrange multiplier based domain decomposition method for implicit time-dependent problems. Int. J. Numer. Methods Eng. 38, 3831–3858 (1995)

    Article  MATH  Google Scholar 

  12. Farhat, C., Roux, F.X.: A method of finite element tearing and interconnecting and its parallel solution algorithm. Int. J. Numer. Methods Eng. 32, 1205–1227 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  13. Fumagalli, A., Scotti, A.: Numerical modeling of multiphase subsurface flow in the presence of fractures. Commun. Appl. Ind. Math. 3, 1–23 (2011)

    MATH  Google Scholar 

  14. Gander, M.J., Halpern, L.: Optimized Schwarz waveform relaxation for advection reaction diffusion problems. SIAM J. Numer. Anal. 45(2), 666–697 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gander, M.J., Halpern, L., Kern, M.: A Schwarz waveform relaxation method for advection–diffusion–reaction problems with continuous coefficients and non-matching grids. In: Domain Decomposition Methods in Science and Engineering XVI, vol. 55 of Lect. Notes Comput. Sci. Eng., pp. 283–290. Springer, Berlin (2007)

  16. Gander, M.J., Japhet, C.: Algorithm 932: PANG: software for nonmatching grid projections in 2D and 3D with linear complexity. ACM Trans. Math. Softw. 40, 25 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  17. Gander, M.J., Japhet, C., Maday, Y., Nataf, F.: A new cement to glue nonconforming grids with Robin interface conditions: the finite element case. In: Domain Decomposition Methods in Science and Engineering. Lect. Notes Comput. Sci. Eng., vol. 40, pp. 259–266. Springer, Berlin (2005)

  18. Gander, M.J., Kwok, F., Mandal, B.C.: Dirichlet–Neumann and Neumann-Neumann waveform relaxation algorithms for parabolic problems. Electron. Trans. Numer. Anal. 45, 424–456 (2016)

    MathSciNet  MATH  Google Scholar 

  19. Gander, M.J., Kwok, F., Mandal, B.C.: Dirichlet–Neumann waveform relaxation methods for parabolic and hyperbolic problems in multiple subdomains. BIT Numer. Math. 1–35 (2020)

  20. Gander, M.J., Hennicker, J., Masson, R.: Modeling and analysis of the coupling in discrete fracture matrix models. SIAM J. Numer. Anal. 59(1), 195–218 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  21. Glowinski, R., Wheeler, M.F.: Domain decomposition and mixed finite element methods for elliptic problems. In: First International Symposium on Domain Decomposition Methods for Partial Differential Equations (Paris, 1987), pp. 144–172. SIAM, Philadelphia, PA (1988)

  22. Halpern, L., Japhet, C., Omnes, P.: Nonconforming in time domain decomposition methods for porous method applications. In: Pereira, J.C.F., Sequeira, A. (eds.) Proceedings of the 5th European Conference on Computational Fluid Dynamics ECCOMAS CFD 2010. Lisbon, Portugal (2010)

  23. Halpern, L., Japhet, C., Szeftel, J.: Optimized Schwarz waveform relaxation and discontinuous Galerkin time stepping for heterogeneous problems. SIAM J. Numer. Anal. 50(5), 2588–2611 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  24. Hoang, T.T.P., Jaffre, J., Japhet, C., Kern, M., Roberts, J.E.: Space-time domain decomposition methods for diffusion problems in mixed formulations. SIAM J. Numer. Anal. 51(6), 3532–3559 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  25. Hoang, T.T.P., Japhet, C., Kern, M., Roberts, J.E.: Space-time domain decomposition for reduced fracture models in mixed formulation. SIAM J. Numer. Anal. 54(1), 288–316 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  26. Hoang, T.T.P., Japhet, C., Kern, M., Roberts, J.E.: Space-time domain decomposition for advection–diffusion problems in mixed formulations. Math. Comput. Simul. 137, 366–389 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  27. Hoang, T.T.P., Lee, H.: A global-in-time domain decomposition methods for the coupled nonlinear Stokes and Darcy flows. J. Sci. Comput. 87(1), 1–22 (2021)

    Article  MathSciNet  Google Scholar 

  28. Jaffre, J., Martin, V., Roberts, J.E.: Modeling fractures and barriers as interfaces for flow in porous media. SIAM J. Sci. Comput. 26, 1667–1691 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  29. Japhet, C., Maday, Y., Nataf, F.: A new interface cement equilibrated mortar method with ventcel conditions. In: Erhel, J., Gander, M., Halpern, L., Pichot, G., Sassi, T., Widlund, O. (eds.) Domain Decomposition Methods in Science and Engineering XXI. Lect. Notes Comput. Sci. Eng., vol. 98, pp. 329–336. Springer (2014)

  30. Japhet, C., Maday, Y.: Mortar methods with optimized transmission conditions for advection–diffusion problems. In: Dickopf, T., Gander, M., Halpern, L., Krause, R., Pavarino, L. (eds.) Domain Decomposition Methods in Science and Engineering XXII. Lecture Notes in Computational Science and Engineering, vol. 104, pp. 541–549. Springer (2016)

  31. Kadeethum, T., Nick, H.M., Lee, S., Ballarin, F.: Flow in porous media with low dimensional fractures by employing enriched Galerkin method. Adv. Water Resour. 142, 103620 (2020)

    Article  Google Scholar 

  32. Kwok, F.: Neumann–Neumann waveform relaxation for the time-dependent heat equation. In: Erhel, J., Gander, M.J., Halpern, L., Pichot, G., Sassi, T., Widlund, O.B. (eds.) Domain Decomposition in Science and Engineering XXI, vol. 98, pp. 189–198. Springer, Berlin (2014)

    Chapter  Google Scholar 

  33. Liesen, J., Strakoš, Z.: Krylov Subspace Methods: Principle and Analysis. Oxford University Press, Oxford (2013)

    MATH  Google Scholar 

  34. Mandal, B.C.: A time-dependent Dirichlet-Neumann method for the heat equation. In: Erhel, J., Gander, M.J., Halpern, L., Pichot, G., Sassi, T., Widlund, O.B. (eds.) Domain Decomposition in Science and Engineering XXI, vol. 98, pp. 467–475. Springer, Berlin (2014)

    Chapter  Google Scholar 

  35. Mandel, J.: Balancing domain decomposition. Commun. Numer. Methods Eng. 9, 233–241 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  36. Mandel, J., Brezina, M.: Balancing domain decomposition for problems with large jumps in coefficients. Math. Comput. 65, 1387–1401 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  37. Martin, V.: An optimized Schwarz waveform relaxation method for the unsteady convection diffusion equation in two dimensions. Appl. Numer. Math. 52, 401–428 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  38. Morales, F., Showalter, R.E.: Interface approximation of Darcy flow in a narrow channel. Math. Methods Appl. Sci. 35, 182–195 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  39. Quarteroni, A., Valli, A.: Theory and application of Steklov–Poincaré operators for boundary-value problems: the heterogeneous operator case. In: Fourth International Symposium on Domain Decomposition Methods for Partial Differential Equations (Moscow, 1990), pp. 58–81. SIAM, Philadelphia, PA (1991)

  40. Quarteroni, A., Valli, A.: Domain Decomposition Method for Partial Differential Equations. Clarendon Press, Oxford (1999)

    MATH  Google Scholar 

  41. Radu, F.A., Suciu, N., Hoffmann, J., Vogel, A., Kolditz, O., Park, C.-H., Attinger, S.: Accuracy of numerical simulations of contaminant transport in heterogeneous aquifers: a comparative study. Adv. Water Resour. 34, 47–61 (2011)

    Article  Google Scholar 

  42. Roberts, J.E., Thomas, J.M.: Mixed and hybrid methods. In: Handbook of Numerical Analysis, Vol. II, Handb. Numer. Anal., II, pp. 523–639. North-Holland, Amsterdam (1991)

  43. Ventcel, A.D.: On boundary conditions for multidimensional diffusion processes. Theory Probab. Appl. 4, 164–177 (1959)

    Article  MATH  Google Scholar 

Download references

Funding

This work is partially supported by the US National Science Foundation under Grant Number DMS-1912626.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Auburn University, Auburn, AL, 36849, USA

    Phuoc-Toan Huynh, Yanzhao Cao & Thi-Thao-Phuong Hoang

Authors
  1. Phuoc-Toan Huynh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yanzhao Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Thi-Thao-Phuong Hoang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Thi-Thao-Phuong Hoang.

Ethics declarations

Competing interests

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huynh, PT., Cao, Y. & Hoang, TTP. Fast and Accuracy-Preserving Domain Decomposition Methods for Reduced Fracture Models with Nonconforming Time Grids. J Sci Comput 96, 23 (2023). https://doi.org/10.1007/s10915-023-02251-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02251-0

Keywords

Mathematics Subject Classification