Skip to main content
Springer Nature Link
Log in

Discontinuous Galerkin Time Stepping for Semilinear Parabolic Problems with Time Constant Delay

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

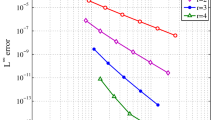
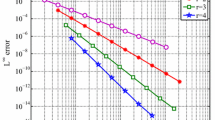
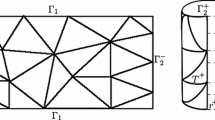
In this paper, a discontinuous Galerkin (DG) time stepping method combined with the standard finite element method in space is proposed to solve a class of semilinear parabolic differential equations with time constant delay. The time semi-discretization and the relevant global convergence of the DG solution under suitable uniform meshes are derived. The standard Galerkin method in space is used to obtain the fully discrete scheme and the optimal global convergence of the full discretization is presented. Numerical experiments for one-dimensional and two-dimensional equations are provided to demonstrate the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Data Availability

Enquiries about data availability should be directed to the authors.

References

  1. Brunner, H., Huang, Q., Xie, H.: Discontinuous Galerkin methods for delay differential equations of pantograph type. SIAM J. Numer. Anal. 48, 1944–1967 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  2. Cockburn, B., Shu, C.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws II: general framework. Math. Comp. 52, 411–435 (1989)

    MathSciNet  MATH  Google Scholar 

  3. Cockburn, B., Shu, C.: Runge–Kutta discontinuous Galerkin methods for conservation domainated problems. J. Sci. Comput. 16, 173–261 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cohen, D., Hagan, P., Simpson, H.: Spatial structures in predator-prey communities with hereditary effects and diffusion. Math. Biosci. 44, 167–177 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  5. Dai, H., huang, Q., Wang, C.: Exponential time differencing-Padé finite element method for nonlinear convection-diffusion-reaction equations with time constant delay. J. Comput. Math. 41, 370–394 (2023)

  6. Delfour, M., Hager, W., Trochu, F.: Discontinuous Galerkin methods for ordinary differential equations. Math. Comp. 36, 455–473 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  7. Eriksson, K., Johnson, C., Thome, V.: Time discretization of parabolic problems by the discontinuous Galerkin method. RAIRO Modél. Math. Anal. Numér. 19, 611–643 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  8. Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems I: a linear model problem. SIAM J. Numer. Anal. 28, 43–77 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  9. Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems II: optimal error estimates in \(L_{\infty } L_2\) and \(L_{\infty } L_{\infty }\). SIAM J. Numer. Anal. 32, 706–740 (1995)

    Article  MathSciNet  Google Scholar 

  10. Higham, D., Sardar, T.: Existence and stability of fixed points for a discretised nonlinear reaction-diffusion equation with delay. Appl. Numer. Math. 18, 155–173 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  11. Huang, C.: Unconditionally stable difference methods for delay partial differential equations. Numer. Math. 122, 579–601 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  12. Huang, C., Vandewalle, S.: An analysis of delay-dependent stability for ordinary and partial differential equations with fixed and distributed delays. SIAM J. Sci. Comput. 25, 1608–1632 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Huang, Q., Li, D., Zhang, J.: Numerical investigations of a class of biological models on unbounded domain. Numer. Math. Theor. Meth. Appl. 12, 169–186 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  14. Huang, Q., Xie, H., Brunner, H.: Superconvergence of discontinuous Galerkin solutions for delay differential equation of pantograph type. SIAM J. Sci. Comput. 33, 2664–2684 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  15. Larsson, S., Thomée, V., Wahlbin, L.: Numerical solution of parabolic integro-differential equations by the discontinuous Galerkin method. Math. Comp. 67, 45–71 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lasaint, P., Raviart, P.A.: On a finite element method for solving the neutron transport equation, mathematical aspects of finite elements in partial differential equations, pp. 89–123. Academic Press, New York (1974)

    Book  MATH  Google Scholar 

  17. Lekomtsev, A., Pimenov, V.: Convergence of the scheme with weights for the numerical solution of a heat conduction equation with delay for the case of variable coefficient of heat conductivity. Appl. Math. Comput. 256, 83–93 (2015)

    MathSciNet  MATH  Google Scholar 

  18. Ling, Z., Lin, Z.: Traveling wavefront in a hematopoiesis model with time delay. Appl. Math. Lett. 23, 426–431 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  19. Li, D., Zhang, C., Qin, H.: LDG method for reaction-diffusion dynamical systems with time delay. Appl. Math. Comput. 217, 9173–9181 (2011)

    MathSciNet  MATH  Google Scholar 

  20. Li, D., Zhang, C.: Superconvergence of a discontinuous Galerkin Method for first-order linear delay differential equations. J. Comput. Math. 29, 574–588 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Liu, Y., Yu, Z., Xia, J.: Exponential stability of traveling waves for non-monotone delayed reaction-diffusion equations. Electron. J. Differ. Eq. 86, 1–15 (2016)

    MathSciNet  MATH  Google Scholar 

  22. Mustapha, K., Brunner, H., Mustapha, H., Schötzau, D.: An \(hp\)-version discontinuous Galerkin method for integro-differential equations of parabolic type. SIAM J. Numer. Anal. 49, 1369–1396 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mustapha, K.: Time-stepping discontinuous Galerkin methods for fractional diffusion problems. Numer. Math. 130, 497–516 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Mustapha, K., Mclean, W.: Superconvergence of a discontinuous Galerkin method for fractional diffusion and wave equations. SIAM J. Numer. Anal. 51, 491–515 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  25. Schötzau, D., Schwab, C.: An \(hp\) a priori error analysis of the DG time-stepping method for initial value problems. Calcolo 37, 207–232 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  26. Schötzau, D., Schwab, C.: Time discretization of parabolic problems by the HP-version of the discontinuous Galerkin finite element method. SIAM J. Numer. Anal. 38, 837–875 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  27. So, W., Yang, Y.: Dirichlet problem for the diffusive Nicholson’s blowflies equation. J. Differ. Equations 150, 317–348 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  28. Sun, Z., Zhang, Z.: A linearized compact difference scheme for a class of nonlinear delay partial differential equations. Appl. Math. Model. 37, 742–752 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  29. Thomée, V.: Galerkin finite element methods for parabolic problems. Springer Verlag, New York (1997)

    Book  MATH  Google Scholar 

  30. Travis, C., Webb, G.: Existence and stability for partial functional differential equations. Dynam. Syst. 200, 147–151 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  31. Wang, P.: Control of parabolic systems with boundary conditions involving time-delays. SIAM J. Control 13, 274–293 (1973)

    Article  MathSciNet  Google Scholar 

  32. Wu, J.: Theory and applications of partial functional differential equations. Springer, New York (1996)

    Book  MATH  Google Scholar 

  33. Zhao, J., Zhan, R., Xu, Y.: Explicit exponential Runge Kutta methods for semilinear parabolic delay differential equations. Math. Comput. Simu. 178, 366–381 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Zubik-Kowal, B.: The method of lines for parabolic differential functional equations. IMA J. Numer. Anal. 17, 103–123 (1997)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first author was supported by Anhui Natural Science Foundation (No. K120131028). The second author was supported by the National Natural Science Foundation of China (No. 11971047) and Beijing Natural Science Foundation (No. Z200002).

Author information

Authors and Affiliations

  1. School of Mathematical Science, Anhui University, Hefei, 230601, China

    Xiuxiu Xu

  2. School of Mathematics, Faculty of Science, Beijing University of Technology, Beijing, 100124, China

    Qiumei Huang

Authors
  1. Xiuxiu Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Qiumei Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qiumei Huang.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, X., Huang, Q. Discontinuous Galerkin Time Stepping for Semilinear Parabolic Problems with Time Constant Delay. J Sci Comput 96, 57 (2023). https://doi.org/10.1007/s10915-023-02278-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02278-3

Keywords

Mathematics Subject Classification