Abstract
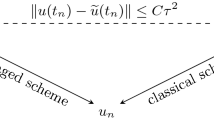
Exponential integrators have been applied successfully in several physics-related differential equations. However, their application in hyperbolic systems with absorbing boundaries, like the ones arising in seismic imaging, still lacks theoretical and experimental investigations. The present work conducts an in-depth study of exponential integration using Faber polynomials, consisting of a generalization of a well-known exponential method that uses Chebyshev polynomials. This allows solving non-symmetric operators that emerge from classic seismic wave propagation problems with absorbing boundaries. Theoretical as well as numerical results are presented for Faber approximations. One of the theoretical contributions is the proposal of a sharp bound for the approximation error of the exponential of a normal matrix. We also show the practical importance of determining an optimal ellipse encompassing the full spectrum of the discrete operator to ensure and enhance the convergence of the Faber exponential series. Furthermore, based on estimates of the spectrum of the discrete operator of the wave equations with a widely used absorbing boundary method, we numerically investigate the stability, dispersion, convergence, and computational efficiency of the Faber exponential scheme. Overall, we conclude that the method is suitable for seismic wave problems and can provide accurate results with large time step sizes, with computational efficiency increasing with the increase of the approximation degree.














Similar content being viewed by others
Data Availibility
All the data used in the paper were synthetically generated, following the instructions on the paper. The data and the computational codes are available in the git-hub link https://github.com/fernanvr/Faber_1D_2D.
Notes
We used the python function ortho_group.rvs from the Python’s package scipy.
References
Al-Mohy, A.H., Higham, N.J.: A new scaling and squaring algorithm for the matrix exponential. SIAM J. Matrix Anal. Appl. 31(3), 970–989 (2010)
Al-Mohy, A.H., Higham, N.J.: Computing the action of the matrix exponential, with an application to exponential integrators. SIAM J. Sci. Comput. 33(2), 488–511 (2011)
Alonso-Mallo, I., Portillo, A.M.: Absorbing boundary conditions and geometric integration: a case study for the wave equation. Math. Comput. Simul. 111, 1–16 (2015)
Assi, H., Cobbold, R.S.: Compact second-order time-domain perfectly matched layer formulation for elastic wave propagation in two dimensions. Math. Mech. Solids 22(1), 20–37 (2017)
Berenger, J.P.: A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 114(2), 185–200 (1994)
Bergamaschi, L., Vianello, M.: Efficient computation of the exponential operator for large, sparse, symmetric matrices. Numer. Linear Algebra Appl. 7(1), 27–45 (2000)
Bergamaschi, L., Caliari, M., Vianello, M.: Efficient approximation of the exponential operator for discrete 2d advection–diffusion problems. Numer. Linear Algebra Appl. 10(3), 271–289 (2003)
Bergamaschi, L., Caliari, M., Vianello, M.: The ReLPM exponential integrator for FE discretizations of advection–diffusion equations. In: International Conference on Computational Science, pp. 434–442. Springer, Berlin (2004)
Brachet, M., Debreu, L., Eldred, C.: Comparison of exponential integrators and traditional time integration schemes for the shallow water equations. Appl. Numer. Math. (2022)
Caliari, M., Vianello, M., Bergamaschi, L.: Interpolating discrete advection–diffusion propagators at Leja sequences. J. Comput. Appl. Math. 172(1), 79–99 (2004)
Calvo, M., Franco, J., Montijano, J., Rández, L.: Explicit Runge–Kutta methods for initial value problems with oscillating solutions. J. Comput. Appl. Math. 76(1–2), 195–212 (1996)
Capizzano, S.S.: Generalized locally Toeplitz sequences: spectral analysis and applications to discretized partial differential equations. Linear Algebra Appl. 366, 371–402 (2003)
Chern, A.: A reflectionless discrete perfectly matched layer. J. Comput. Phys. 381, 91–109 (2019)
Cohen, D., Dujardin, G.: Exponential integrators for nonlinear Schrödinger equations with white noise dispersion. Stoch. Partial Differ. Equ. Anal. Comput. 5(4), 592–613 (2017)
Cox, S.M., Matthews, P.C.: Exponential time differencing for stiff systems. J. Comput. Phys. 176(2), 430–455 (2002)
Deka, P.J., Einkemmer, L.: Efficient adaptive step size control for exponential integrators. Comput. Math. Appl. 123, 59–74 (2022)
Garoni, C., Serra-Capizzano, S., et al.: Generalized Locally Toeplitz Sequences: Theory and Applications, vol. 1. Springer, Berlin (2017)
Gaudreault, S., Rainwater, G., Tokman, M.: Kiops: A fast adaptive Krylov subspace solver for exponential integrators (vol 372, pg 236, 2018). J. Comput. Phys. 441 (2021)
Higham, N.J.: The scaling and squaring method for the matrix exponential revisited. SIAM J. Matrix Anal. Appl. 26(4), 1179–1193 (2005)
Hochbruck, M., Ostermann, A.: Exponential integrators. Acta Numer. 19, 209–286 (2010)
Huber, D., Schreiber, M., Schulz, M.: Graph-based multi-core higher-order time integration of linear autonomous partial differential equations. J. Comput. Sci. (2021). https://doi.org/10.1016/j.jocs.2021.101349
Ikelle, L.T., Amundsen, L.: Introduction to petroleum seismology. Soc. Explor. Geophys. (2018)
Jackiewicz, Z., Renaut, R.: A note on stability of pseudospectral methods for wave propagation. J. Comput. Appl. Math. 143(1), 127–139 (2002)
Jing, H., Chen, Y., Wang, J., Xue, W.: A highly efficient time-space-domain optimized method with Lax-Wendroff type time discretization for the scalar wave equation. J. Comput. Phys. 393, 1–28 (2019)
Kole, J.: Solving seismic wave propagation in elastic media using the matrix exponential approach. Wave Motion 38(4), 279–293 (2003)
Leveque, R.: Finite Difference Methods for Differential Equations (1998)
Liu, Y.: Globally optimal finite-difference schemes based on least squares. Geophysics 78(4), T113–T132 (2013)
Loffeld, J., Tokman, M.: Comparative performance of exponential, implicit, and explicit integrators for stiff systems of odes. J. Comput. Appl. Math. 241, 45–67 (2013)
Moler, C., Van Loan, C.: Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 45(1), 3–49 (2003)
Moret, I., Novati, P.: The computation of functions of matrices by truncated Faber series. Numer. Funct. Anal. Optim. (2001)
Munch, N.J.: A Chebyshev theorem for ellipses in the complex plane. Am. Math. Mon. 126(5), 430–436 (2019)
Nakamura, S., Tadano, Y.: On a continuum limit of discrete Schrodinger operators on square lattices. J. Spectr. Theory 11(1), 355–368 (2021)
Niesen, J., Wright, W.: A Krylov subspace algorithm for evaluating the \(\varphi \)-functions in exponential integrators. arXiv preprint arXiv:0907.4631 (2009)
Pototschnig, M., Niegemann, J., Tkeshelashvili, L., Busch, K.: Time-domain simulations of the nonlinear Maxwell equations using operator-exponential methods. IEEE Trans. Antennas Propag. 57(2), 475–483 (2009)
Ramadan, M.A., Raslan, K.R., El Danaf, T.S., Abd El Salam, M.A.: An exponential Chebyshev second kind approximation for solving high-order ordinary differential equations in unbounded domains, with application to Dawson’s integral. J. Egypt. Math. Soc. 25(2), 197–205 (2017)
Schreiber, M., Schaeffer, N., Loft, R.: Exponential integrators with parallel-in-time rational approximations for the shallow-water equations on the rotating sphere. Parallel Comput. 85, 56–65 (2019)
Sidje, R.B.: Expokit: A software package for computing matrix exponentials. ACM Trans. Math. Softw. (TOMS) 24(1), 130–156 (1998)
Starke, G., Varga, R.S.: A hybrid Arnoldi–Faber iterative method for nonsymmetric systems of linear equations. Numer. Math. 64(1), 213–240 (1993)
Strikwerda, J.C.: Finite Difference Schemes and Partial Differential Equations. SIAM (2004)
Tago, J., Cruz-Atienza, V., Chaljub, E., Brossier, R., Coutant, O., Garambois, S., Prieux, V., Operto, S., Mercerat, D., Virieux, J., et al.: Modelling seismic wave propagation for geophysical imaging. In: Seismic waves-Research and Analysis. IntechOpen (2012)
Wang, Y., Liang, W., Nashed, Z., Li, X., Liang, G., Yang, C.: Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship-preserving method. Geophysics 79(5), T277–T285 (2014)
Welzl, E.: Smallest enclosing disks (balls and ellipsoids). In: New Results and New Trends in Computer Science: Graz, Austria, June 20–21, 1991 Proceedings. Springer, Berlin (2005)
Wilcox, L.C., Stadler, G., Burstedde, C., Ghattas, O.: A high-order discontinuous Galerkin method for wave propagation through coupled elastic-acoustic media. J. Comput. Phys. 229(24), 9373–9396 (2010)
Zhang, X., Yang, D., Song, G.: A nearly analytic exponential time difference method for solving 2d seismic wave equations. Earthq. Sci. 27(1), 57–77 (2014)
Acknowledgements
The authors gratefully acknowledge the support of the financial institutions that contributed to this research.
Funding
This research was conducted in collaboration with the R &D project registered as ANP20714-2 at the Brazilian National Agency for Petroleum, Natural Gas, and Biofuels (ANP) for Software Technologies for Modelling and Inversion (STMI), with applications in seismic imaging (USP/Shell Brasil/ANP). Partial funding was provided by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES - Coordination of Superior Level Staff Improvement) - Brazil - Finance Code 001 and by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq - National Council for Scientific and Technological Development) - Brazil. The São Paulo Research Foundation (FAPESP), Grant 2021/06176-0, is also acknowledged. Additionally, this research has received partial funding from the Federal Ministry of Education and Research and the European High-Performance Computing Joint Undertaking (JU) under grant agreement No 955701, Time-X. The JU receives support from the European Union’s Horizon 2020 research and innovation programme and Belgium, France, Germany, Switzerland.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Appendix
A Appendix
1.1 Appendix A.1: Continuous Framework
We formally write the equations formulations, with PML conditions, used throughout the work. For 1D the domain \(\varOmega =[a_1,a_2]\) is an interval and for 2D \(\varOmega =[0,a_2]\times [0,b_2]\) is considered a square. The particular values of \(a_1\) and \(a_2\) are fixed in the numerical tests.
One dimensional acoustic waves with PML:
-
1.
Using second order spatial derivatives (2SD)
$$\begin{aligned} \frac{\partial u}{\partial t}(x,t)&=v(x,t), \end{aligned}$$(36)$$\begin{aligned} \frac{\partial v}{\partial t}(x,t)&=-\beta _x(x)v(x,t)+c^2(x)\left( \frac{\partial ^2 u}{\partial x^2}(x,t)+\frac{\partial w}{\partial x}(x,t)\right) +f(x,t), \end{aligned}$$(37)$$\begin{aligned} \frac{\partial w}{\partial t}(x,t)&=-\beta _x(x)\left( w(x,t)+\frac{\partial u}{\partial x}(x,t)\right) . \end{aligned}$$(38) -
2.
Using only first order spatial derivatives [13] (1SD)
$$\begin{aligned} \frac{\partial u}{\partial t}(x,t)&=c^2(x)\left( \frac{\partial v}{\partial x}(x,t) - w(x,t)\right) +\int \limits _{t_0}^t f(x,s)ds, \end{aligned}$$(39)$$\begin{aligned} \frac{\partial v}{\partial t}(x,t)&=-\beta _x(x)v(x,t)+\frac{\partial u}{\partial x}(x,t), \end{aligned}$$(40)$$\begin{aligned} \frac{\partial w}{\partial t}(x,t)&=\beta _x(x)\left( -w(x,t)+\frac{\partial v}{\partial x}(x,t)\right) . \end{aligned}$$(41)
Two dimension acoustic waves with PML:
-
1.
Using second order spatial derivatives (2SD)
$$\begin{aligned} \frac{\partial u}{\partial t}(x,y,t)&=v(x,y,t),\end{aligned}$$(42)$$\begin{aligned} \frac{\partial v}{\partial t}(x,y,t)&=-\big (\beta _x(x)+\beta _y(y)\big )v(x,y,t)-\beta _x(x)\beta _y(y)u(x,y,t)\nonumber \\&\quad +c^2(x,y)\left( \frac{\partial ^2 u}{\partial x^2}(x,y,t)+\frac{\partial ^2 u}{\partial y^2}(x,y,t)+\frac{\partial w_x}{\partial x}(x,y,t)\right. \nonumber \\&\quad \left. +\frac{\partial w_y}{\partial y}(x,y,t)\right) +f(x,y,t), \end{aligned}$$(43)$$\begin{aligned} \frac{\partial w_x}{\partial t}(x,y,t)&=-\beta _x(x)w_x(x,y,t)+(\beta _y(y)-\beta _x(x))\frac{\partial u}{\partial x}(x,y,t), \end{aligned}$$(44)$$\begin{aligned} \frac{\partial w_y}{\partial t}(x,y,t)&=-\beta _y(y)w_y(x,y,t)+(\beta _x(x)-\beta _y(y))\frac{\partial u}{\partial y}(x,y,t). \end{aligned}$$(45) -
2.
Using only first order spatial derivatives [13] (1SD)
$$\begin{aligned} \frac{\partial u}{\partial t}(x,y,t)&=c^2(x,y)\bigg (\frac{\partial v_x}{\partial x}(x,y,t) +\frac{\partial v_y}{\partial y}(x,y,t) -w_x(x,y,t)\nonumber \\&\quad -w_y(x,y,t)\bigg )+\int \limits _{t_0}^tf(x,y,s)ds, \end{aligned}$$(46)$$\begin{aligned} \frac{\partial v_x}{\partial t}(x,y,t)&=-\beta _x(x)v_x(x,y,t)+\frac{\partial u}{\partial x}(x,y,t), \end{aligned}$$(47)$$\begin{aligned} \frac{\partial v_y}{\partial t}(x,y,t)&=-\beta _y(y)v_y(x,y,t)+\frac{\partial u}{\partial y}(x,y,t), \end{aligned}$$(48)$$\begin{aligned} \frac{\partial w_x}{\partial t}(x,y,t)&=\beta _x(x)\left( -w_x(x,y,t)+\frac{\partial v_x}{\partial x}(x,y,t)\right) , \end{aligned}$$(49)$$\begin{aligned} \frac{\partial w_y}{\partial t}(x,y,t)&=\beta _y(y)\left( -w_y(x,y,t)+\frac{\partial v_y}{\partial y}(x,y,t)\right) . \end{aligned}$$(50)
Two-dimensional elastic waves with PML, see Assi and Cobbold [4]:
with the variables and parameters described in Table 2.
The damping functions \(\beta _z\), related to the absorption factor are defined as
where \(d(z,\partial \varOmega )\) is the distance from z to the boundary of \(\varOmega \), \(\delta \) is the thickness of the PML domain, \(\beta _0\) is the magnitude of the absorption factor, and \(\varOmega _1\) is the numerical domain without the damping layer (physical domain). Thus, \(\varOmega \) is composed by the union of \(\varOmega _1\) and a damping layer of thickness \(\delta \) extending on the boundary of \(\varOmega _1\).
1.2 A.2: Discrete Framework
The spatial discretizations are based on a staggered grid using 4th and 8th order approximation of the spatial derivatives defined by Eqs. (20) and (21). Figures 15 and 16 describe the discrete space for the 1SD and 2SD formulation in 1D, and the 2SD and elastic formulations in 2D, respectively.
1.3 A.3: Numerical Benchmarks
We define the numerical experiments, called “Test Case” used through the paper. In all the tests we use a zero Dirichlet condition on the boundary of the domain \(\varOmega \), a PML layer thickness of \(\delta =0.8\,\text {km}\), a damping parameter \(\beta _0=30\), and Ricker peak frequency of \(f_0=25\,\text {Hz}\). If not otherwise stated, the initial condition for all the variables is zero. The particular benchmarks are then defined as follows:
Test Case #1: \(\varOmega =[0,10.5\,\text {km}]\)
Test Case #2: \(\varOmega =[0,10.5\,\text {km}]\)
Test Case #3: \(\varOmega =[0,10.5\,\text {km}]\)
Test Case #4: \(\varOmega =[0,8\;\text {km}]\times [0,8\;\text {km}]\)
Test Case #5: \(\varOmega =[0,8\;\text {km}]\times [0,8\;\text {km}]\)
Test Case #6: \(\varOmega =[0,8\;\text {km}]\times [0,8\;\text {km}]\)
Test Case #7: \(\varOmega =[0,8\;\text {km}]\times [0,8\;\text {km}]\) for elastic waves
1.4 A.4: Spectrum Complementary Results
In this subsection, we present the spectral distribution results using the 2SD formulation, along with the real and imaginary limits of the spectrum for the elastic equations with PML.
Eigenvalues on the complex plane (using coordinates \(({\textit{Re}}(\lambda ), {\textit{Im}}(\lambda ))\)) using a fourth-order spatial discretization of the acoustic wave equation in one dimension, with formulation 2SD, considering TC#3, for \(\varDelta x=\{0.105,0.021,0.0105,0.0021\}\). For each \(\varDelta x\), spectrum, the spectrum has a rectangular-shaped convex hull
Based on Fig. 17, it is evident that besides \(\sigma ({\varvec{H}})\) being symmetric with respect to the real axis, the limits of the rectangle on the imaginary axis appear to have a linear relationship with \(1/\varDelta x\). However, for the real part, the relationship is different, exhibiting a constant negative limit on the left side (\(-\beta _0\)) for the PML parameter \(\beta _0>0\), and a small positive number on the right. In general, we observed similar results for other formulations (Fig. 18).
For the acoustic 2SD equations, empirical studies, as the one shown in Fig. 6, indicate that the upper bound is a positive small number, smaller than 1. Since in all experiments this upper bound is always close to zero, this will not affect the estimates of the optimal ellipse for Faber polynomial approximations, as the ellipse size will be dominated by the imaginary axis bounds and the lower bound in the real axis. Therefore, a precise upper real bound will not be further required.
1.5 A.5: Stability and Dispersion
Here we present the operators and results of stability and dispersion for all the systems of equations considered in Section A.2 (assuming no PML and no source term), with a spatial discretization of fourth and eighth orders. At the end of the section are also presented the graphics of stability and dispersion of the elastic formulation (Figs. 19 and 20).
-
1.
1SD and 2SD in one dimension
$$\begin{aligned} \varDelta t{\varvec{H}}=\frac{c\varDelta t}{\varDelta x}\begin{pmatrix} 0&{}g_{11}\\ g_{21}&{}0 \end{pmatrix},\quad \varDelta t{\varvec{H}}=\frac{c\varDelta t}{\varDelta x}\begin{pmatrix} 0&{}1\\ h_{11}&{}0 \end{pmatrix}. \end{aligned}$$ -
2.
1SD and 2SD in two dimension
$$\begin{aligned} \varDelta t{\varvec{H}}=\frac{c\varDelta t}{\varDelta x}\begin{pmatrix} 0&{}g_{11}&{}g_{12}\\ g_{21}&{}0&{}0\\ g_{22}&{}0&{}0 \end{pmatrix},\quad \varDelta t{\varvec{H}}=\frac{c\varDelta t}{\varDelta x}\begin{pmatrix} 0&{}1\\ h_{11}+h_{22}&{}0 \end{pmatrix}. \end{aligned}$$ -
3.
Elastic in two dimension (without considering the decoupled two first equations)
$$\begin{aligned} \varDelta t{\varvec{H}}=\frac{\varDelta t}{\varDelta x}\frac{2\mu +\lambda }{\rho }\begin{pmatrix} 0&{}0&{}\frac{1}{2\mu +\lambda }g_{11}&{}\frac{1}{2\mu +\lambda }g_{12}&{}0\\ 0&{}0&{}0&{}\frac{1}{2\mu +\lambda }g_{21}&{}\frac{1}{2\mu +\lambda }g_{22}\\ \rho g_{21}&{}\frac{\rho \lambda }{2\mu +\lambda } g_{12}&{}0&{}0&{}0\\ \frac{\rho \mu }{2\mu +\lambda } g_{22}&{}\frac{\rho \mu }{2\mu +\lambda } g_{11}&{}0&{}0&{}0\\ \frac{\rho \lambda }{2\mu +\lambda } g_{21}&{}\rho g_{12}&{}0&{}0&{}0 \end{pmatrix}. \end{aligned}$$
Where
-
1.
For 4th order
$$\begin{aligned} g_{11}&=\frac{1}{24}\left( 27(1-e^{-ik_x\varDelta x})+e^{-2k_x\varDelta x}-e^{k_x\varDelta x}\right) \\ g_{12}&=\frac{1}{24}\left( 27(1-e^{-ik_y\varDelta x})+e^{-2k_y\varDelta x}-e^{k_y\varDelta x}\right) \\ g_{21}&=\frac{1}{24}\left( 27(e^{ik_x\varDelta x}-1)+e^{-k_x\varDelta x}-e^{2k_x\varDelta x}\right) \\ g_{22}&=\frac{1}{24}\left( 27(e^{ik_x\varDelta x}-1)+e^{-k_x\varDelta x}-e^{2k_x\varDelta x}\right) \\ h_{11}&=-\frac{1}{6}\cos (2\theta _x)+\frac{8}{3}\cos (\theta _x)-\frac{5}{2}\\ h_{22}&=-\frac{1}{6}\cos (2\theta _y)+\frac{8}{3}\cos (\theta _y)-\frac{5}{2} \end{aligned}$$ -
2.
For 8th order
$$\begin{aligned} g_{11}&=\frac{1225}{1024}\left( 1-e^{-ik_x\varDelta x}+\frac{1}{15}(e^{-2k_x\varDelta x}-e^{k_x\varDelta x})+\frac{1}{125}(e^{2k_x\varDelta x}-e^{-3k_x\varDelta x})\right. \\&\quad \left. +\frac{1}{1715}(e^{-4k_x\varDelta x}-e^{3k_x\varDelta x})\right) \\ g_{12}&=\frac{1225}{1024}\left( 1-e^{-ik_y\varDelta x}+\frac{1}{15}(e^{-2k_y\varDelta x}-e^{k_y\varDelta x})+\frac{1}{125}(e^{2k_y\varDelta x}-e^{-3k_y\varDelta x})\right. \\&\quad \left. +\frac{1}{1715}(e^{-4k_y\varDelta x}-e^{3k_y\varDelta x})\right) \\ g_{21}&=\frac{1225}{1024}\left( e^{ik_x\varDelta x}-1+\frac{1}{15}(e^{-k_x\varDelta x}-e^{2k_x\varDelta x})+\frac{1}{125}(e^{3k_x\varDelta x}-e^{-2k_x\varDelta x})\right. \\&\quad \left. +\frac{1}{1715}(e^{-3k_x\varDelta x}-e^{4k_x\varDelta x})\right) \\ g_{22}&=\frac{1225}{1024}\left( e^{ik_y\varDelta x}-1+\frac{1}{15}(e^{-k_y\varDelta x}-e^{2k_y\varDelta x})+\frac{1}{125}(e^{3k_y\varDelta x}-e^{-2k_y\varDelta x})\right. \\&\quad \left. +\frac{1}{1715}(e^{-3k_y\varDelta x}-e^{4k_y\varDelta x})\right) \\ h_{11}&=-\frac{1}{560}(e^{-4k_x\varDelta x}+e^{4k_x\varDelta x})+\frac{8}{315}(e^{-3k_x\varDelta x}+e^{3k_x\varDelta x})-\frac{1}{5}(e^{-2k_x\varDelta x}+e^{2k_x\varDelta x})\\&\quad +\frac{8}{5}(e^{-k_x\varDelta x}+e^{k_x\varDelta x})-\frac{205}{72}\\ h_{22}&=-\frac{1}{560}(e^{-4k_y\varDelta x}+e^{4k_y\varDelta x})+\frac{8}{315}(e^{-3k_y\varDelta x}+e^{3k_y\varDelta x})-\frac{1}{5}(e^{-2k_y\varDelta x}+e^{2k_y\varDelta x})\\&\quad +\frac{8}{5}(e^{-k_y\varDelta x}+e^{k_y\varDelta x})-\frac{205}{72} \end{aligned}$$
Stability graphics of the Faber approximation method for different spatial discretizations, and polynomial degrees \(m=\{3,4,\ldots ,40\}\), for the elastic formulation. The CFL number (left), and the measure of the operations number of Eq. (33) (right). Higher polynomial degrees implies in larger \(c_{\text {CFL}}\), but this does not necessarily results in a decrease of the MVOs
1.6 A.6: Convergence
In this section, we detail the construction of the RK(9-7) scheme employed for computing the reference solution. Furthermore, we provide the convergence and computational efficiency results achieved through the utilization of Faber polynomials in solving elastic wave propagation equations (Figs. 21 and 22).
RK(9-7) algorithm:
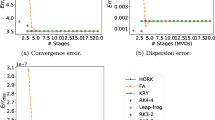
Approximation error of Faber polynomials using the elastic equations, to solve TC#7. The curves represent the error when using polynomial of degrees \(m=\{5,10,\dots ,25\}\). Increasing the degree of the polynomial allows for larger steps in time, while keeping the approximation error smaller than a fixed threshold
Convergence in polynomial order for the elastic equations, using different spatial discretization orders, and a wide range of polynomial degrees. The maximum \(\varDelta t\) such that the error of Faber approximations is less than \(10^{-6}\) is shown on the right. On the left, we show the number of operations using the values of \(\varDelta t_{\text {max}}\) of the upper line. When the polynomial degree increases, the maximum allowed time-step size also increases, together with a decrease of the number of operations
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ravelo, F.V., Peixoto, P.S. & Schreiber, M. An Explicit Exponential Integrator Based on Faber Polynomials and its Application to Seismic Wave Modeling. J Sci Comput 98, 32 (2024). https://doi.org/10.1007/s10915-023-02413-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02413-0