Skip to main content
Springer Nature Link
Log in

A New S-M Limiter Entropy Stable Scheme Based on Moving Mesh Method for Ideal MHD and SWMHD Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

For magnetohydrodynamics (MHD) equations, the existing entropy stable (ES) flux effectively eliminates the spurious oscillation, but it still has potential for improvement such as the resolution of discontinuous solutions. We propose a high-resolution scheme based on a moving mesh strategy for approximating solutions of ideal MHD and shallow water MHD (SWMHD) in this paper. Firstly, a new S-M flux limiter is constructed to weigh the ES flux and the anti-diffusive flux to obtain a new flux with high resolution and entropy stability properties. By adjusting the amplitude of anti-diffusive flux adaptively, the new flux can reduce its dissipation in smooth regions and increase dissipation at discontinuities, which is more consistent with physical laws. Secondly, we introduce the moving mesh strategy to optimize mesh generation and eliminate the defects of structured mesh. A new monitor function is defined to identify structural features of solutions at each particular time level and to assign appropriate weights to all regions with large numerical solution gradients, to construct a mesh evolution equation and increase the mesh density of these regions. Finally, we combine the moving mesh strategy with the high-resolution ES scheme and evaluate more accurate solutions according to the order of “mesh redistribution-update of solution-equation solving on new mesh”. Numerical results show that the new algorithm can achieve strong robustness and high resolution, and can track various waves effectively (especially the shock and rarefaction waves).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

The datasets generated and analysed during the current study are available from the corresponding author on reasonable request.

References

  1. Balbás, J., Tadmor, E.: A central differencing simulation of the Orszag-Tang vortex system. IEEE Trans. Plasma Sci. 33(2), 470–471 (2005)

    Article  ADS  Google Scholar 

  2. Balsara, D.S.: Multidimensional HLLE Riemann solver: application to Euler and magnetohydrodynamic flows. J. Comput. Phys. 229(6), 1970–1993 (2010)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  3. Balsara, D.S., Spicer, D.S.: A staggered mesh algorithm using high order Godunov fluxes to ensure solenoidal magnetic fields in magnetohydrodynamic simulations. J. Comput. Phys. 149(2), 270–292 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  4. Barmin, A., Kulikovskiy, A., Pogorelov, N.: Shock-capturing approach and nonevolutionary solutions in magnetohydrodynamics. J. Comput. Phys. 126(1), 77–90 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  5. Brio, M., Wu, C.: An upwind differencing scheme for the equations of ideal magnetohydrodynamics. J. Comput. Phys. 75(2), 400–422 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  6. Cao, W., Huang, W., Russell, R.D.: A study of monitor functions for two-dimensional adaptive mesh generation. SIAM J. Sci. Comput. 20(6), 1978–1994 (1999)

    Article  MathSciNet  Google Scholar 

  7. Christlieb, A.J., Rossmanith, J.A., Tang, Q.: Finite difference weighted essentially non-oscillatory schemes with constrained transport for ideal magnetohydrodynamics. J. Comput. Phys. 268, 302–325 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  8. Dai, W., Woodward, P.R.: An approximate Riemann solver for ideal magnetohydrodynamics. J. Comput. Phys. 111(2), 354–372 (1994)

    Article  ADS  Google Scholar 

  9. De Sterck, H.: Hyperbolic theory of the “shallow water’’ magnetohydrodynamics equations. Phys. Plasmas 8(7), 3293–3304 (2001)

    Article  ADS  MathSciNet  Google Scholar 

  10. Dedner, A., Kemm, F., Kröner, D., Munz, C.D., Schnitzer, T., Wesenberg, M.: Hyperbolic divergence cleaning for the MHD equations. J. Comput. Phys. 175(2), 645–673 (2002)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  11. Duan, J., Tang, H.: High-order accurate entropy stable finite difference schemes for the shallow water magnetohydrodynamics. J. Comput. Phys. 431, 110136 (2021)

    Article  MathSciNet  Google Scholar 

  12. Fu, L., Tang, Q.: High-order low-dissipation targeted ENO schemes for ideal magnetohydrodynamics. J. Sci. Comput. 80(1), 692–716 (2019)

    Article  MathSciNet  Google Scholar 

  13. Gilman, P.A.: Magnetohydrodynamic shallow water equations for the solar tachocline. Astrophys. J. 544(1), 79–82 (2000)

    Article  ADS  Google Scholar 

  14. Gottlieb, S., Ketcheson, D.I., Shu, C.W.: High order strong stability preserving time discretizations. J. Sci. Comput. 38(3), 251–289 (2009)

    Article  MathSciNet  Google Scholar 

  15. Gu, Y., Luo, D., null, Z.G., Chen, Y.: An adaptive moving mesh method for the five-equation model. Commun. Comput. Phys. 32, 189–221 (2022)

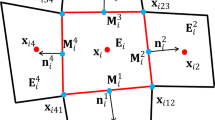
    Article  MathSciNet  Google Scholar 

  16. Han, J., Tang, H.: An adaptive moving mesh method for two-dimensional ideal magnetohydrodynamics. J. Comput. Phys. 220(2), 791–812 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  17. Harten, A.: High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49(3), 357–393 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  18. Harten, A., Hyman, J.M.: Self adjusting grid methods for one-dimensional hyperbolic conservation laws. J. Comput. Phys. 50(2), 235–269 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  19. Ismail, F., Roe, P.L.: Affordable, entropy-consistent Euler flux functions ii: Entropy production at shocks. J. Comput. Phys. 228(15), 5410–5436 (2009)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  20. Jeffrey, A., Taniuti, T.: Non-linear Wave Propagation with Applications to Physics and Magnetohydrodynamics. Academic Press, New York (2000)

    Google Scholar 

  21. Jiang, G., Wu, C.: A high-order WENO finite difference scheme for the equations of ideal magnetohydrodynamics. J. Comput. Phys. 150, 561–594 (1999)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  22. Kemm, F.: Roe-type schemes for shallow water magnetohydrodynamics with hyperbolic divergence cleaning. Appl. Math. Comput. 272, 385–402 (2016)

    MathSciNet  Google Scholar 

  23. Kurganov, A., Qu, Z., Rozanova, O.S., Wu, T.: Adaptive moving mesh central-upwind schemes for hyperbolic system of PDEs: Applications to compressible Euler equations and granular hydrodynamics. Commun. Appl. Math. Comput. 3(3), 445–479 (2021)

    Article  MathSciNet  Google Scholar 

  24. Kurganov, A., Qu, Z., Wu, T.: Well-balanced positivity preserving adaptive moving mesh central-upwind schemes for the Saint-Venant system. ESAIM-Math. Model. Numer. Anal.-Model. Math. Anal. Numer. 56(4), 1327–1360 (2022)

    Article  MathSciNet  Google Scholar 

  25. Lax, P.D.: Weak solutions of nonlinear hyperbolic equations and their numerical computation. Commun. Pure Appl. Math. 7(1), 159–193 (1954)

    Article  MathSciNet  Google Scholar 

  26. Lax, P.D.: Hyperbolic systems of conservation laws and the mathematical theory of shock waves. Society for Industrial and Applied Mathematics, America (1973)

  27. Liu, Y., Feng, J., Ren, J.: High resolution, entropy-consistent scheme using flux limiter for hyperbolic systems of conservation laws. J. Sci. Comput. 64(3), 914–937 (2015)

    Article  MathSciNet  Google Scholar 

  28. Osher, S., Chakravarthy, S.: High resolution schemes and the entropy condition. SIAM J. Numer. Anal. 21(5), 955–984 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  29. Prabhat, M., Kumar, D.R.: A novel moving mesh technique for scalar hyperbolic conservation law. AIP Conf. Proc. 2336(1), 030014 (2021)

    Article  Google Scholar 

  30. Roe, P.: Entropy conservative schemes for Euler equations. Talk at HYP 2006, Lyon, France (2006)

  31. Roe, P.L.: Some contributions to the modelling of discontinuous flows. Large-scale computations in fluid mechanics, pp. 163–193 (1985)

  32. Rossmanith, J.A.: A Wave Propagation Method with Constrained Transport for Ideal and Shallow Water Magnetohydrodynamics. University of Washington, Washington (2002)

    Google Scholar 

  33. Spiegel, E.A., Zahn, J.P.: The solar tachocline. Astron. Astrophys. 265, 106–114 (1992)

    ADS  Google Scholar 

  34. Susanto, A., Ivan, L., De Sterck, H., Groth, C.: High-order central ENO finite-volume scheme for ideal MHD. J. Comput. Phys. 250, 141–164 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  35. Sweby, P., Baines, M.: On convergence of Roe’s scheme for the general non-linear scalar wave equation. J. Comput. Phys. 56(1), 135–148 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  36. Sweby, P.K.: High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 21(5), 995–1011 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  37. Tadmor, E.: The numerical viscosity of entropy stable schemes for systems of conservation laws. i. Math. Comput. 49(179), 91–103 (1987)

    Article  MathSciNet  Google Scholar 

  38. Tang, H., Tang, T.: Adaptive mesh methods for one-and two-dimensional hyperbolic conservation laws. SIAM J. Numer. Anal. 41(2), 487–515 (2003)

    Article  MathSciNet  Google Scholar 

  39. Toro, E.F.: Shock-Capturing Methods for Free Surface Shallow Flows. Wiley, New York (2001)

    Google Scholar 

  40. Toro, E.F.: Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer, Berlin (2013)

    Google Scholar 

  41. Torrilhon, M.: Uniqueness conditions for Riemann problems of ideal magnetohydrodynamics. J. Plasma Phys. 69(3), 253–276 (2003)

    Article  ADS  CAS  Google Scholar 

  42. Touma, R.: Unstaggered central schemes with constrained transport treatment for ideal and shallow water magnetohydrodynamics. Appl. Numer. Math. 60(7), 752–766 (2010)

    Article  MathSciNet  Google Scholar 

  43. Van Leer, B.: Towards the ultimate conservative difference scheme . ii. Monotonicity and conservation combined in a second-order scheme. J. Comput. Phys. 14(4), 361–370 (1974)

    Article  ADS  Google Scholar 

  44. Winters, A.R., Gassner, G.J.: Affordable, entropy conserving and entropy stable flux functions for the ideal MHD equations. J. Comput. Phys. 304, 72–108 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  45. Winters, A.R., Gassner, G.J.: An entropy stable finite volume scheme for the equations of shallow water magnetohydrodynamics. J. Sci. Comput. 67(2), 514–539 (2016)

    Article  MathSciNet  Google Scholar 

  46. Xu, J., Su, H., Li, Z.: Optimal convergence of three iterative methods based on nonconforming finite element discretization for 2d/3d MHD equations. Numer. Algorithms. 90(3), 1117–1151 (2022)

    Article  MathSciNet  Google Scholar 

  47. Xu, X., Gao, Z., Dai, Z.: A 3d staggered Lagrangian scheme for ideal magnetohydrodynamics on unstructured meshes. Int. J. Numer. Methods Fluids. 90(11), 584–602 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  48. Yang, X., Huang, W., Qiu, J.: A moving mesh WENO method for one-dimensional conservation laws. SIAM J. Sci. Comput. 34(4), A2317–A2343 (2012)

    Article  MathSciNet  Google Scholar 

  49. Yee, H.C., Sjögreen, B.: Efficient low dissipative high order schemes for multiscale MHD flows, ii: Minimization of \(\nabla \cdot \) B numerical error. J. Sci. Comput. 29(1), 115–164 (2006)

    Article  MathSciNet  Google Scholar 

  50. Zachary, A.L., Colellaz, P.: A higher-order Godunov method for the equations of ideal magnetohydrodynamics. J. Comput. Phys. 99(2), 341–347 (1992)

    Article  ADS  Google Scholar 

  51. Zhang, M., Huang, W., Qiu, J.: A well-balanced positivity-preserving quasi-Lagrange moving mesh DG method for the shallow water equations. Commun. Comput. Phys. 31, 94–130 (2022)

    Article  MathSciNet  Google Scholar 

  52. Zia, S., Ahmed, M., Qamar, S.: Numerical solution of shallow water magnetohydrodynamic equations with non-flat bottom topography. Int. J. Comput. Fluid Dyn. 28(1–2), 56–75 (2014)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

All authors are grateful to Professor Yulong Xing of Ohio State University for his useful comments and helpful suggestions.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Number [11971075]).

Author information

Authors and Affiliations

  1. College of Science, Chang’an University, Xi’an, 710064, Shaanxi, China

    Mengqing Zhai, Supei Zheng, Chengzhi Zhang & Mangmang Jian

Authors
  1. Mengqing Zhai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Supei Zheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Chengzhi Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Mangmang Jian
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Mengqing Zhai derived the scheme, did the numerical experiments, wrote the main manuscript text, and prepared all the figures. Supei Zheng provided the original data and programs, and reviewed and edited the manuscript. Chengzhi Zhang did several two-dimensional experiments and provided numerical results. All authors reviewed the manuscript.

Corresponding author

Correspondence to Supei Zheng.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhai, M., Zheng, S., Zhang, C. et al. A New S-M Limiter Entropy Stable Scheme Based on Moving Mesh Method for Ideal MHD and SWMHD Equations. J Sci Comput 98, 68 (2024). https://doi.org/10.1007/s10915-024-02458-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-024-02458-9

Keywords

Mathematics Subject Classification