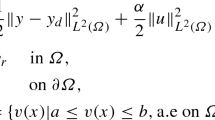Abstract
In this paper, sparse elliptic PDE-constrained optimization problems with \(L^{1-2}\)-control cost (\(L^{1-2}\)-EOCP) are considered. To induce control sparsity, traditional finite element models usually use \(L^{1}\)-control cost to induce sparsity, and in practical problems, many non-convex regularization terms are more capable of inducing sparsity than convex regularization terms, for example, in finite-dimensional problems, the sparsity of \(l_{1-2}\)-norm induced solutions is stronger than \(l_{1}\)-norm. Inspired by the finite-dimensional problems, we extend the \(L^{1-2}\)-regularization technique to infinite-dimensional elliptic PDE-constrained optimization problems. Unlike finite-dimensional problems where the \(l_{1-2}\)-norm is greater than or equal to 0, the conclusion does not hold for the \(L^{1-2}\)-control cost in the infinite-dimensional sense. To overcome these difficulties, an inexact difference of convex functions algorithm with sieving strategy (s-iDCA) is proposed for solving \(L^{1-2}\)-EOCP where the corresponding subproblems are solved by an inexact heterogeneous alternating direction method of multipliers (ihADMM) algorithm. Furthermore, by using the particular structure of the \(L^{1-2}\)-EOCP and constructing a new energy function and using its KŁ property, the global convergence results of the DCA algorithm are given. Numerical experiments show that our proposed s-iDCA algorithm is effective and that the model with the \(L^{1-2}\)-regularization term is stronger than the \(L^{1}\)-regularization term in terms of the sparsity of the induced solutions.









Similar content being viewed by others
Data Availability
The data that support the findings of this study are available on request from the corresponding author.
References
Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. 116, 5–16 (2009)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the kurdyka-łojasiewicz inequality. Math. Oper. Res. 35(2), 438–457 (2010)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized gauss-seidel methods. Math. Program. 137(1–2), 91–129 (2013)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2(1), 183–202 (2009)
Bergounioux, M., Kunisch, K.: Primal–dual strategy for state-constrained optimal control problems. Comput. Optim. Appl. 22(2), 193–224 (2002)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1–2, Ser. A), 459–494 (2014)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1–2), 459–494 (2014)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J., et al.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends ® Mach. Learn. 3(1), 1–122 (2011)
Casas, E., Herzog, R., Wachsmuth, G.: Approximation of sparse controls in semilinear equations by piecewise linear functions. Numer. Math. 122(4), 645–669 (2012)
Casas, E., Herzog, R., Wachsmuth, G.: Optimality conditions and error analysis of semilinear elliptic control problems with \(L^1\) cost functional. SIAM J. Optim. 22(3), 795–820 (2012)
Chen, L., Sun, D., Toh, K.-C.: An efficient inexact symmetric Gauss–Seidel based majorized ADMM for high-dimensional convex composite conic programming. Math. Program. 161(1–2), 237–270 (2017)
Clason, C., Kunisch, K.: A duality-based approach to elliptic control problems in non-reflexive Banach spaces. ESAIM Control Optim. Calc. Var. 17(1), 243–266 (2011)
Ding, M., Song, X., Bo, Yu.: An inexact proximal dc algorithm with sieving strategy for rank constrained least squares semidefinite programming. J. Sci. Comput. 91(3), 75 (2022)
Efron, B., Hastie, T., Johnstone, I., Tibshirani, R.: Least angle regression. Ann. Statist. 32(2), 407–499 (2004)
Esser, E., Lou, Y., Xin, J.: A method for finding structured sparse solutions to nonnegative least squares problems with applications. SIAM J. Imag. Sci. 6(4), 2010–2046 (2013)
Fazel, M., Pong, T.K., Sun, D., Tseng, P.: Hankel matrix rank minimization with applications to system identification and realization. SIAM J. Matrix Anal. Appl. 34(3), 946–977 (2013)
Hintermüller, M., Ito, K., Kunisch, K.: The primal–dual active set strategy as a semismooth newton method. SIAM J. Optim. 13(3), 865–888 (2002)
Hinze, M., Pinnau, R., Ulbrich, M., Ulbrich, S.: Optimization with PDE constraints. In: Barth, T.J., et al. (eds.) Mathematical Modelling: Theory and Applications, vol. 23. Springer, New York (2009)
Ito, K., Kunisch, K.: Lagrange Multiplier Approach to Variational Problems and Applications, volume 15 of Advances in Design and Control. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2008)
Jiang, K., Sun, D., Toh, K.-C.: An inexact accelerated proximal gradient method for large scale linearly constrained convex SDP. SIAM J. Optim. 22(3), 1042–1064 (2012)
Kurdyka, K.: On gradients of functions definable in o-minimal structures. Annales de l’institut Fourier 48, 769–783 (1998)
Li, X., Sun, D., Toh, K.-C.: A Schur complement based semi-proximal ADMM for convex quadratic conic programming and extensions. Math. Program. 155(1–2), 333–373 (2016)
Li, X., Sun, D., Toh, K.-C.: QSDPNAL: A two-phase augmented Lagrangian method for convex quadratic semidefinite programming. Math. Program. Comput. 10(4), 703–743 (2018)
Lojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels. Les équations aux dérivées partielles 117, 87–89 (1963)
Lou, Y., Yan, M.: Fast \(\ell _{1-2}\) minimization via a proximal operator. J. Sci. Comput. 74(2), 767–785 (2018)
Nesterov, Yu.: Smooth minimization of non-smooth functions. Math. Program. 103, 127–152 (2005)
Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course, vol. 87. Springer, Berlin (2003)
Pan, Y.: Distributed optimization and statistical learning for large-scale penalized expectile regression. J. Korean Statist. Soc. 50(1), 290–314 (2021)
Pearson, J.W., Wathen, A.J.: A new approximation of the Schur complement in preconditioners for PDE-constrained optimization. Numer. Linear Algebra Appl. 19(5), 816–829 (2012)
Porcelli, M., Simoncini, V., Stoll, M.: Preconditioning PDE-constrained optimization with \(L^1\)-sparsity and control constraints. Comput. Math. Appl. Int. J. 74(5), 1059–1075 (2017)
Schindele, A., Borzi, A.: Proximal methods for elliptic optimal control problems with sparsity cost functional. Appl. Math. 7(9), 967–992 (2016)
Simoncini, V.: A new iterative method for solving large-scale Lyapunov matrix equations. SIAM J. Sci. Comput. 29(3), 1268–1288 (2007)
Song, X., Chen, B., Yu, B.: Mesh independence of an accelerated block coordinate descent method for sparse optimal control problems. arXiv preprint arXiv:1709.00005 (2017)
Song, X., Yu, B.: A two-phase strategy for control constrained elliptic optimal control problems. Numer. Linear Algebra Appl. 25(4), e2138 (2018)
Song, X., Bo, Yu., Wang, Y., Zhang, X.: An FE-inexact heterogeneous ADMM for elliptic optimal control problems with \(L^1\)-control cost. J. Syst. Sci. Complex. 31(6), 1659–1697 (2018)
Stadler, G.: Elliptic optimal control problems with \(L^1\)-control cost and applications for the placement of control devices. Comput. Optim. Appl. Int. J. 44(2), 159–181 (2009)
Tao, P.D., An, L.T.H.: Convex analysis approach to DC programming: theory, algorithms and applications. Acta mathematica vietnamica 22(1), 289–355 (1997)
Tao, P.D., An, L.T.H.: A DC optimization algorithm for solving the trust-region subproblem. SIAM J. Optim. 8(2), 476–505 (1998)
Tao, P.D., et al.: Algorithms for solving a class of nonconvex optimization problems methods of subgradients. In: North-Holland Mathematics Studies, vol. 129, pp. 249–271. Elsevier, Amsterdam (1986)
Tao, P.D., et al.: Numerical solution for optimization over the efficient set by DC optimization algorithms. Oper. Res. Lett. 19(3), 117–128 (1996)
Tao, P.D., et al.: A branch and bound method via DC optimization algorithms and ellipsoidal technique for box constrained nonconvex quadratic problems. J. Glob. Optim. 13(2), 171–206 (1998)
Toh, K.-C., Yun, S.: An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems. Pac. J. Optim. 6(615–640), 15 (2010)
Tseng, P.: On accelerated proximal gradient methods for convex–concave optimization. SIAM J. Optim. 2(3), 1–20 (2008)
Ulbrich, M.: Semismooth Newton methods for operator equations in function spaces. SIAM J. Optim. 13(3), 805–842 (2003)
Ulbrich, M.: Semismooth Newton Methods for Variational Inequalities and Constrained Optimization Problems in Function Spaces, volume 11 of MOS-SIAM Series on Optimization. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2011)
Urruty, J.-B.H., Lemaréchal, C.: Convex Analysis and Minimization Algorithms. Springer, Berlin (1993)
Wachsmuth, G., Wachsmuth, D.: Convergence and regularization results for optimal control problems with sparsity functional. ESAIM Control Optim. Calc. Var. 17(3), 858–886 (2011)
Yao, Q., Kwok, J.T., Guo, X.: Fast learning with nonconvex \(\ell _{1-2}\) regularization using the proximal gradient algorithm. arXiv preprint arXiv:1610.09461 (2016)
Yin, P., Lou, Y., He, Q., Xin, J.: Minimization of \(\ell _{1-2}\) for compressed sensing. SIAM J. Sci. Comput. 37(1), A536–A563 (2015)
Zhu, L., Wang, J., He, X., Zhao, Y.: An inertial projection neural network for sparse signal reconstruction via \(\ell _{1-2}\) minimization. Neurocomputing 315, 89–95 (2018)
Zulehner, W.: Analysis of iterative methods for saddle point problems: a unified approach. Math. Comput. 71(238), 479–505 (2002)
Acknowledgements
The authors thank the anonymous reviewers for their valuable suggestions.
Funding
This work is supported by the National Key R &D Program of China (Grand No. 2023YFA1011303), and the National Natural Science Foundation of China (NSF: #11571061, #1197011770, and #12301479).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
KŁ Property
We next recall the Kurdyka–Łojasiewicz (KŁ) property, which is satisfied by many functions such as proper closed semialgebraic functions, and is important for analyzing global sequential convergence and local convergence rate of first-order methods; see, for example, [1,2,3]. For notational simplicity, for any \(a\in (0, \infty ]\), we let \(\varXi _{a}\) denote the set of all concave continuous functions \(\varphi :[0, a)\rightarrow [0, \infty )\) that are continuously differentiable on (0, a) with positive derivatives and satisfy \(\varphi (0)=0\).
Definition 1
(KŁ property and KŁ exponent) A proper closed function h is said to satisfy the KŁ property at \(\bar{{{\textbf {x}}}}\in dom\partial h\) if there exist \(a\in (0, \infty ], \varphi \in \varXi _{a}\) and a neighborhood U of \(\bar{{{\textbf {x}}}}\) such that
whenever \({{\textbf {x}}}\in U\) and \(h(\bar{{{\textbf {x}}}})<h({{\textbf {x}}})<h(\bar{{{\textbf {x}}}})+a\). If h satisfies the KŁ property at \(\bar{{{\textbf {x}}}}\in dom\partial h\) and the \(\varphi \) in (A.1) can be chosen as \(\varphi (s)=cs^{1-\alpha }\) for some \(\alpha \in [0, 1)\) and \(c>0\), then we say that h satisfies the KŁ property at \(\bar{{{\textbf {x}}}}\) with exponent \(\alpha \). We say that h is a KŁ function if h satisfies the KŁ property at all points in \(dom\partial h\), and say that h is a KŁ function with exponent \(\alpha \in [0, 1)\) if h satisfies the KŁ property with exponent \(\alpha \) at all points in \(dom\partial h\).
The following lemma was proved in [7], which concerns the uniformized KŁ property. This property is useful for establishing convergence of first-order methods for level-bounded functions.
Lemma 1
(Uniformized KŁ property) Suppose that h is a proper closed function and let \(\varGamma \) be a compact set. If h is a constant on \(\varGamma \) and satisfies the KŁ property at each point of \(\varGamma \), then there exist \(\epsilon , a>0\), and \(\varphi \in \varXi _{a}\) such that
for any \(\hat{{{\textbf {x}}}}\in \varGamma \) and any \({{\textbf {x}}}\) satisfying \(dist({{\textbf {x}}}, \varGamma )<\epsilon \) and \(h(\hat{{{\textbf {x}}}})<h({{\textbf {x}}})<h(\hat{{{\textbf {x}}}})+a\).
Proof of Theorem 3
In the view of Theorem 2 (1), it suffices to prove that \(\{u^{k_{l}}\}\) is convergent and \(\sum ^{\infty }_{l=1}\Vert u^{k_{l}}-u^{k_{l-1}}\Vert _{L^{2}}<\infty \). To this end, we first recall form Proposition 1 (3) and (2.13) that the sequence \(\{E(u^{k_{l}},\xi ^{k_{l}})\}\) is non-increasing and \(\zeta =\lim _{l\rightarrow \infty }E(u^{k_{l}},\xi ^{k_{l}})\) exists. Thus, if there exists some \(N>0\) such that \(E(u^{N},\xi ^{N})=\zeta \), then it must hold that \(E(u^{k_{l}},\xi ^{k_{l}})=\zeta \) for all \(k_{l}\ge N\). Therefor, we know that form (2.13) that \(u^{k_{l}}=u^{N}\) for any \(k_{l}\ge N\), implying that \(\{u^{k_{l}}\}\) converges finitely.
We next consider the case that \(E(u^{k_{l}},\xi ^{k_{l}})>\zeta \) for all \(k_{l}\). Recall from Proposition 1 (2) that \(\varUpsilon \) is the (compact) set of accumulation points of \(\{(u^{k_{l}},\xi ^{k_{l}})\}\). Since E satisfies the KŁ property at each point in the compact set \(\varUpsilon \subseteq dom\partial E\) and \(E\equiv \zeta \) on \(\varUpsilon \), by E satisfies the KŁ property, there exist an \(\epsilon >0\) and a continuous concave function \(\varphi \in \varXi _{a}\) with \(a>0\) such that
for all \((u,w)\in W\), where
Since \(\varUpsilon \) is the set of the accumulation points of the bounded sequence \(\{(u^{k_{l}},\xi ^{k_{l}})\}\), we have
Hence, there exists \(N_{1}>0\) such that \(dist((u^{k_{l}^{1}},\xi ^{k_{l}^{1}}), \varUpsilon )<\epsilon \) for any \(k_{l}\ge N_{1}\). In addition, since the sequence \(\{E(u^{k_{l}},\xi ^{k_{l}})\}\) converges to \(\zeta \) by the Proposition 1 (3), there exists \(N_{2}>0\) such that \(\zeta<E(u^{k_{l}},\xi ^{k_{l}})<\zeta +a\) for any \(k_{l}\ge N_{2}\). Let \({\bar{N}}=\max \{N_{1}, N_{2}\}\). Then the sequence \(\{(u^{k_{l}},\xi ^{k_{l}})\}_{k_{l}\ge {\bar{N}}}\) belongs to W and we deduce from (A.1) that
This makes sense since we know that \(E(u^{k_{l}},\xi ^{k_{l}})>E(u^{k_{l+1}},\xi ^{k_{l+1}})\) for any \(k_{l}>l\). From Proposition 1 we get that
On the other hand, from the concavity of \(\varphi \) we get that
For convenience, we define for all \(p,q\in N\) the following quantities
and
Combining Proposition 1 with (B.3) and (B.4) yields for any \(k>l\) that
and hence
Using the fact that \(2\sqrt{\alpha \beta }\le \alpha +\beta \) for all \(\alpha ,\beta \ge 0\), we infer
Let us now prove that for any \(k>m\) the following inequality holds
Summing up (B.5) for \(i=m+1,\ldots ,k\) yields
where the last inequality follows from the fact that \(\varDelta _{p,q}+\varDelta _{q,r}=\varDelta _{p,r}\) for all \(p,q,r\in N\). Since \(\varphi \ge 0\), we thus have for any \(k>m\) that
This easily shows that the sequence \(\{u^{k_{l}}\}_{k_{l}\in N}\) has finite length, that is,
It is clear that (B.6) implies that the sequence \(\{u^{k_{l}}\}_{k_{l}\in N}\) is a Cauchy sequence and hence is a convergent sequence. Indeed, with \(q>p>m\) we have
hence
Since (B.6) implies that \(\sum ^{\infty }_{k=m+1}\Vert u^{k_{l+1}}-u^{k_{l}}\Vert _{L^{2}}\) converges to zero as \(m\rightarrow \infty \), it follows that \(\{u^{k_{l}}\}_{k_{l}\in N}\) is a Cauchy sequence and hence is a convergent sequence. The completes the proof.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, Y., Song, X., Yu, B. et al. An iDCA with Sieving Strategy for PDE-Constrained Optimization Problems with \(L^{1-2}\)-Control Cost. J Sci Comput 99, 24 (2024). https://doi.org/10.1007/s10915-024-02489-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02489-2